Monte-Carlo Tree Search
Home * Search * Monte-Carlo Tree Search
Monte Carlo Tree Search, (Monte-Carlo Tree Search, MCTS)
is a Best-First search algorithm, historically based on random playouts. In conjunction with UCT (Upper Confidence bounds applied to Trees) Monte-Carlo Tree Search has yielded in a breakthrough in Computer Go [2], and is also successful in Amazons [3] [4], Lines of Action [5], Havannah [6], Hex [7], Checkers [8] and other Games with some difficulties in position evaluation, but until December 2017, when a Google DeepMind team reported on AlphaZero [9], not for Chess [10] [11].
MCTS is based on randomized explorations of the search space. Using the results of previous explorations, the algorithm gradually grows a game tree in memory, and successively becomes better at accurately estimating the values of the most promising moves [12].
Contents
Four Phases
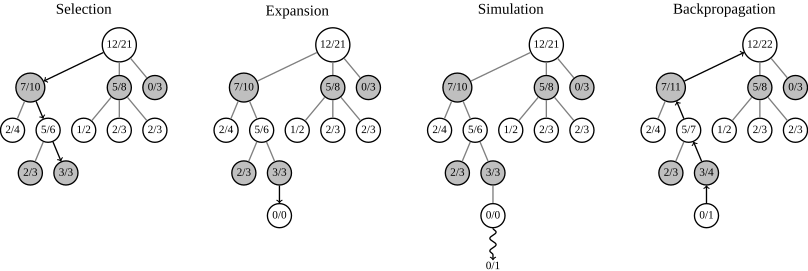
MCTS consists of four strategic phases, repeated as long as there is time left [13] :
- In the Selection phase the tree is traversed from the root node until it selects a leaf node that is not added to the tree yet
- The Expansion strategy adds the leaf node to the tree
- The Simulation strategy plays moves in self-play until the end of the game. The result is either 1, 0 ,-1
- The Backpropagation strategy propagates the results through the tree
Steps of Monte Carlo Tree Search [14]
Pure Monte-Carlo search
Pure Monte-Carlo search with parameter T means that for each feasible move T random games are generated. The move with the best average score is played. A game is called “Monte Carlo perfect” when this procedure converges to perfect play for each position, when T goes to infinity. However, with limited time per move, increasing T does not guarantee to find a better move [15].
UCT
UCT (Upper Confidence bounds applied to Trees) deals with the flaw of Monte-Carlo Tree Search, when a program may favor a losing move with only one or a few forced refutations, but due to the vast majority of other moves provides a better random playout score than other, better moves [16]. In UCT, upper confidence bounds guide the selection of a node, treating selection as a {https://en.wikipedia.org/wiki/Multi-armed_bandit multi-armed bandit] problem. PUCT modifies the original policy by approximately predicting good arms at the start of a sequence of multi-armed bandit trials [17].
Playouts by NN
Historically, at the root of MCTS were random and noisy playouts. Many such playouts were necessary to accurately evaluate a state. Since AlphaGo and AlphaZero it is not the case anymore. Strong policies and evaluations are now provided by neural networks that are trained with Reinforcement Learning. In AlphaGo and its descendants the policy is used as a prior in the PUCT bandit to explore first the most promising moves advised by the neural network policy and the evaluations replace the playouts [18].
See also
- Category:MCTS
- Deep Learning
- MCαβ
- MC and UCT poster by Jakob Erdmann
- Rollout Paradigm
- Sampling-Based Planning
- Simulated Annealing
- UCT
Publications
1987
- Bruce Abramson, Richard Korf (1987). A Model of Two-Player Evaluation Functions. AAAI-87, pdf
1990 ...
- Bruce Abramson (1990). Expected-Outcome: A General Model of Static Evaluation. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 12, No. 2
- Bruce Abramson (1990). An Analysis of Expected-Outcome. Journal of Experimental and Theoretical Artificial Intelligence, Vol. 2
- Bruce Abramson (1991). The Expected-Outcome Model of Two-Player Games. Part of the series, Research Notes in Artificial Intelligence, Morgan Kaufmann
- Bernd Brügmann (1993). Monte Carlo Go. pdf
2000 ...
- Bruno Bouzy, Bernard Helmstetter (2003). Monte Carlo Go Developments. Advances in Computer Games 10, pdf
- Bruno Bouzy (2004). Associating Shallow and Selective Global Tree Search with Monte Carlo for 9 × 9 Go. CG 2004
- Tristan Cazenave (2004). Monte Carlo Real Time Strategy. pdf
2005 ...
- Tristan Cazenave, Bernard Helmstetter (2005). Combining tactical search and Monte-Carlo in the game of Go. IEEE CIG 2005, pdf, pdf
- Bruno Bouzy (2005). Move-Pruning Techniques for Monte-Carlo Go. Advances in Computer Games 11
- Bruno Bouzy (2005). Associating domain-dependent knowledge and Monte Carlo approaches within a go program. Information Sciences, Heuristic Search and Computer Game Playing IV
2006
- Levente Kocsis, Csaba Szepesvári (2006). Bandit based Monte-Carlo Planning ECML-06, LNCS/LNAI 4212, pp. 282-293. introducing UCT, pdf
- Sylvain Gelly, Yizao Wang (2006). Exploration exploitation in Go: UCT for Monte-Carlo Go. pdf
- Sylvain Gelly, Yizao Wang, Rémi Munos, Olivier Teytaud (2006). Modification of UCT with Patterns in Monte-Carlo Go. INRIA
- Levente Kocsis, Csaba Szepesvári, Jan Willemson (2006). Improved Monte-Carlo Search. pdf
- Jahn-Takeshi Saito, Guillaume Chaslot, Jos Uiterwijk, Jaap van den Herik (2006). Monte-Carlo Proof-Number Search for Computer Go. CG 2006
- Rémi Coulom (2006). Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search. CG 2006
- Bruno Bouzy (2006). History and Territory Heuristics for Monte-Carlo Go. New Mathematics and Natural Computation
- Haruhiro Yoshimoto, Kazuki Yoshizoe, Tomoyuki Kaneko, Akihiro Kishimoto, Kenjiro Taura (2006). Monte Carlo Go Has a Way to Go. AAAI 2006, pdf
2007
- Rémi Coulom (2007). Monte-Carlo Tree Search in Crazy Stone. slides as pdf
- Yizao Wang, Sylvain Gelly (2007). Modifications of UCT and Sequence-Like Simulations for Monte-Carlo Go. IEEE Symposium on Computational Intelligence and Games, Honolulu, USA, 2007, pdf
- Shugo Nakamura, Makoto Miwa, Takashi Chikayama (2007). Improvement of UCT using evaluation function. 12th Game Programming Workshop 2007
- Ken Chen, Peigang Zhang (2007). Monte-Carlo Go with Knowledge-Guided Simulations. CGW 2007
- Tristan Cazenave (2007). Reflexive Monte-Carlo Search. CGW 2007, pdf [19]
- François van Lishout, Guillaume Chaslot, Jos Uiterwijk (2007). Monte-Carlo Tree Search in Backgammon. CGW 2007
- Julien Kloetzer, Hiroyuki Iida, Bruno Bouzy (2007). The Monte-Carlo approach in Amazons. CGW 2007
- Tristan Cazenave, Nicolas Jouandeau (2007). On the Parallelization of UCT. CGW 2007, pdf
- Jahn-Takeshi Saito, Mark Winands, Jos Uiterwijk, Jaap van den Herik (2007). Grouping Nodes for Monte-Carlo Tree Search. CGW 2007
- Tristan Cazenave (2007). Evolving Monte-Carlo Tree Search Algorithms. pdf
- Pim Nijssen (2007). Playing Othello Using Monte Carlo. Bachelor's Thesis, Maastricht University, pdf
2008
- Ken Chen, Peigang Zhang (2008). Monte-Carlo Go with Knowledge-Guided Simulations. ICGA Journal, Vol. 31, No. 2
- Sylvain Gelly, Jean-Baptiste Hoock, Arpad Rimmel, Olivier Teytaud, Yann Kalemkarian (2008). The Parallelization of Monte-Carlo Planning - Parallelization of MC-Planning. ICINCO-ICSO 2008: 244-249, pdf, slides as pdf
- Guillaume Chaslot, Louis Chatriot, Christophe Fiter, Sylvain Gelly, Jean-Baptiste Hoock, Julien Pérez, Arpad Rimmel, Olivier Teytaud (2008). Combining expert, offline, transient and online knowledge in Monte-Carlo exploration. pdf
- Guillaume Chaslot, Mark Winands, Jos Uiterwijk, Jaap van den Herik, Bruno Bouzy (2008). Progressive Strategies for Monte-Carlo Tree Search. New Mathematics and Natural Computation, Vol. 4, No. 3, pdf [20]
- Guillaume Chaslot, Sander Bakkes, István Szita, Pieter Spronck (2008). Monte-Carlo Tree Search: A New Framework for Game AI. pdf
- Guillaume Chaslot, Mark Winands, István Szita, Jaap van den Herik. (2008). Cross-entropy for Monte-Carlo Tree Search. ICGA Journal, Vol. 31, No. 3, pdf
- Maarten Schadd, Mark Winands, Jaap van den Herik, Huib Aldewereld (2008). Addressing NP-Complete Puzzles with Monte-Carlo Methods. In Volume 9: Proceedings of the AISB 2008 Symposium on Logic and the Simulation of Interaction and Reasoning, pages 55-61, Brighton, UK, 2008. The Society for the study of Artificial Intelligence and Simulation of Behaviour. pdf
- Maarten Schadd, Mark Winands, Jaap van den Herik, Guillaume Chaslot, Jos Uiterwijk (2008). Single-Player Monte-Carlo Tree Search. CG 2008, pdf
- Richard J. Lorentz (2008). Amazons Discover Monte-Carlo. CG 2008
- Mark Winands, Yngvi Björnsson, Jahn-Takeshi Saito (2008). Monte-Carlo Tree Search Solver. CG 2008, pdf
- Nathan Sturtevant (2008). An Analysis of UCT in Multi-player Games. CG 2008
- Guillaume Chaslot, Mark Winands, Jaap van den Herik (2008). Parallel Monte-Carlo Tree Search. CG 2008, pdf
- Tristan Cazenave, Nicolas Jouandeau (2008). A Parallel Monte-Carlo Tree Search Algorithm. CG 2008, pdf
- Ken Chen, Dawei Du, Peigang Zhang (2008). A Fast Indexing Method for Monte-Carlo Go. CG 2008
- Yizao Wang, Jean-Yves Audibert, Rémi Munos (2008). Algorithms for Infinitely Many-Armed Bandits. Advances in Neural Information Processing Systems, pdf, Supplemental material - pdf
- James H. Brodeur, Benjamin E. Childs, Levente Kocsis (2008). Transpositions and Move Groups in Monte Carlo Tree Search. pdf
- Hilmar Finnsson, Yngvi Björnsson. (2008). Simulation-Based Approach to General Game Playing. In The Twenty-Third AAAI Conference on Artificial Intelligence, AAAI Press, 2008. Accepted. pdf, pdf » General Game Playing
- Jean Méhat, Tristan Cazenave (2008). Monte-Carlo Tree Search for General Game Playing. pdf » General Game Playing
- Tristan Cazenave, Nicolas Jouandeau (2008). A Parallel Monte-Carlo Tree Search Algorithm. pdf
- Ingo Althöfer (2008). On the Laziness of Monte-Carlo Game Tree Search in Non-tight Situations. Technical Report, pdf
- Kazutomo Shibahara, Yoshiyuki Kotani (2008). Combining Final Score with Winning Percentage using Sigmoid Function in Monte-Carlo Algorithm. 13th Game Programming Workshop, pdf
- Shogo Takeuchi, Tomoyuki Kaneko, Kazunori Yamaguchi (2008). Evaluation of Monte Carlo tree search and the application to Go. CIG 2008
2009
- Jean-Yves Audibert, Rémi Munos, Csaba Szepesvári (2009). Exploration-exploitation trade-off using variance estimates in multi-armed bandits. Theoretical Computer Science, 410:1876-1902, 2009, pdf
- Guillaume Chaslot, Christophe Fiter, Jean-Baptiste Hoock, Arpad Rimmel, Olivier Teytaud (2009). Adding Expert Knowledge and Exploration in Monte-Carlo Tree Search. Advances in Computer Games 12, pdf, pdf
- Guillaume Chaslot, Jean-Baptiste Hoock, Julien Pérez, Arpad Rimmel, Olivier Teytaud, Mark Winands (2009). Meta Monte-Carlo Tree Search for Automatic Opening Book Generation. pdf
- Markus Enzenberger, Martin Müller (2009). A lock-free multithreaded Monte-Carlo tree search algorithm, Advances in Computer Games 12, pdf
- Rémi Coulom (2009). The Monte-Carlo Revolution in Go. JFFoS'2008: Japanese-French Frontiers of Science Symposium, slides as pdf
- Mark Winands, Yngvi Björnsson (2009). Evaluation Function Based Monte-Carlo LOA. pdf [21]
- Tristan Cazenave (2009). Nested Monte-Carlo Search. IJCAI 2009, pdf
- Paolo Ciancarini, Gian Piero Favini (2009). Monte Carlo Tree Search Techniques in the Game of Kriegspiel. IJCAI 2009, pdf » KriegSpiel
- Tristan Cazenave (2009). Monte-Carlo Kakuro. Advances in Computer Games 12, pdf
- István Szita, Guillaume Chaslot, Pieter Spronck (2009). Monte-Carlo Tree Search in Settlers of Catan. Advances in Computer Games 12, pdf [22]
- Tristan Cazenave, Nicolas Jouandeau (2009). Parallel Nested Monte-Carlo Search. NIDISC 2009, pdf
- Tomas Kozelek (2009). Methods of MCTS and the game Arimaa. Master's thesis, pdf » Arimaa
- Kenta Sasaki, Yoshiyuki Kotani (2009). Monte-Carlo Tree Search in the Game of Blokus-Duo. 14th Game Programming Workshop [23]
- David Silver, Gerald Tesauro (2009). Monte-Carlo Simulation Balancing. ICML 2009, pdf
- Ken Chen, Dawei Du, Peigang Zhang (2009). Monte-Carlo Tree Search and Computer Go. Advances in Information and Intelligent Systems 2009
- David Silver (2009). Reinforcement Learning and Simulation-Based Search. Ph.D. thesis, University of Alberta, pdf
- Seth Pellegrino, Andrew Hubbard, Jason Galbraith, Peter D. Drake, Yung-Pin Chen (2009). Localizing Search in Monte-Carlo Go using Statistical Covariance. ICGA Journal, Vol. 32, No. 3
2010 ...
- Julien Kloetzer (2010). Monte-Carlo Techniques: Applications to the Game of the Amazons. Ph.D. thesis, JAIST
- Yoshikuni Sato, Daisuke Takahashi, Reijer Grimbergen (2010). A Shogi Program based on Monte-Carlo Tree Search. ICGA Journal, Vol. 33, No. 2
- Richard J. Lorentz (2010). Improving Monte-Carlo Tree Search in Havannah. CG 2010
- Amine Bourki, Guillaume Chaslot, Matthieu Coulm, Vincent Danjean, Hassen Doghmen, Thomas Hérault, Jean-Baptiste Hoock, Arpad Rimmel, Fabien Teytaud, Olivier Teytaud, Paul Vayssière, Ziqin Yu (2010). Scalability and Parallelization of Monte-Carlo Tree Search. CG 2010, pdf
- Julien Kloetzer (2010). Monte-Carlo Opening Books for Amazons. CG 2010
- Arpad Rimmel, Fabien Teytaud, Olivier Teytaud (2010). Biasing Monte-Carlo Simulations through RAVE Values. CG 2010, pdf
- Jean-Yves Audibert (2010). PAC-Bayesian aggregation and multi-armed bandits. Habilitation thesis, Université Paris Est, pdf, slides as pdf
- Shih-Chieh Huang, Rémi Coulom, Shun-Shii Lin (2010). Monte-Carlo Simulation Balancing in Practice. CG 2010, pdf
- Tristan Cazenave, Abdallah Saffidine (2010). Score Bounded Monte-Carlo Tree Search. CG 2010, pdf
- Pim Nijssen, Mark Winands (2010). Enhancements for Multi-Player Monte-Carlo Tree Search. CG 2010, pdf
- Raghuram Ramanujan, Ashish Sabharwal, Bart Selman (2010). On Adversarial Search Spaces and Sampling-Based Planning. ICAPS 2010 [24]
- Shih-Chieh Huang, Rémi Coulom, Shun-Shii Lin (2010). Monte-Carlo Simulation Balancing applied to 9x9 Go. ICGA Journal, Vol. 33, No. 4
- Tristan Cazenave, Abdallah Saffidine (2010). Monte-Carlo Hex. pdf
- Jean Méhat, Tristan Cazenave (2010). Combining UCT and Nested Monte-Carlo Search for Single-Player General Game Playing. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 2, No. 4, pdf 2009 » General Game Playing
- Broderick Arneson, Ryan Hayward, Philip Henderson (2010). Monte Carlo Tree Search in Hex. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 2, No. 4, pdf
- Mark Winands, Yngvi Björnsson, Jahn-Takeshi Saito (2010). Monte Carlo Tree Search in Lines of Action. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 2, No. 4, pdf
- Hendrik Baier, Peter D. Drake (2010). The power of forgetting: Improving the last-good-reply policy in Monte Carlo Go. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 2, No. 4
- Ingo Althöfer (2010). Game Self-Play with Pure Monte-Carlo: The Basin Structure. pdf
- Fabien Teytaud, Olivier Teytaud (2010). On the Huge Benefit of Decisive Moves in Monte-Carlo Tree Search Algorithms. pdf
- Guillaume Chaslot (2010). Monte-Carlo Tree Search. Ph.D. Thesis, Maastricht University, pdf
- Jahn-Takeshi Saito (2010). Solving Difficult Game Positions. Ph.D. Thesis, Maastricht University, pdf
- Romaric Gaudel, Michèle Sebag (2010). Feature Selection as a one-player game. ICML 2010, pdf
- Hendrik Baier (2010). Adaptive Playout Policies for Monte-Carlo Go. Master's thesis, University of Osnabrück, pdf
- Thomas J. Walsh, Sergiu Goschin, Michael L. Littman (2010). Integrating sample-based planning and model-based reinforcement learning. AAAI, pdf » UCT, Reinforcement Learning
2011
- Markus Enzenberger, Martin Müller, Broderick Arneson, Richard Segal (2011). Fuego - An Open-source Framework for Board Games and Go Engine Based on Monte-Carlo Tree Search. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 2, No. 4, pdf
- Christopher D. Rosin (2011). Multi-armed bandits with episode context. Annals of Mathematics and Artificial Intelligence, Vol. 61, No. 3, ISAIM 2010 pdf
- Shih-Chieh Huang, Rémi Coulom, Shun-Shii Lin (2011). Time Management for Monte-Carlo Tree Search Applied to the Game of Go. TAAI 2010, pdf
- Arpad Rimmel, Fabien Teytaud, Tristan Cazenave (2011). Optimization of the Nested Monte-Carlo Algorithm on the Traveling Salesman Problem with Time Windows. Evostar 2011, pdf
- Cameron Browne (2011). The Dangers of Random Playouts. ICGA Journal, Vol. 34, No. 1
- Jean Méhat, Tristan Cazenave (2011). A Parallel General Game Player. KI Journal, Vol. 25, No. 1, pdf
- Shih-Chieh Huang (2011). New Heuristics for Monte Carlo Tree Search Applied to the Game of Go. Ph.D. thesis, pdf
- Petr Baudiš (2011). Information Sharing in MCTS. Master thesis, Faculty of Mathematics and Physics, Charles University in Prague, pdf
- Petr Baudiš (2011). Balancing MCTS by Dynamically Adjusting the Komi Value. ICGA Journal, Vol. 34, No. 3
- Richard J. Lorentz (2011). Experiments with Monte-Carlo Tree Search in the Game of Havannah. ICGA Journal, Vol. 34, No. 3
- Kazuki Yoshizoe, Akihiro Kishimoto, Tomoyuki Kaneko, Haruhiro Yoshimoto, Yutaka Ishikawa (2011). Scalable Distributed Monte Carlo Tree Search. SoCS2011, pdf
- Cheng-Wei Chou, Olivier Teytaud, Shi-Jim Yen (2011). Revisiting Monte-Carlo Tree Search on a Normal Form Game: NoGo. EvoApplications 2011 [25]
- Shi-Jim Yen, Jung-Kuei Yang (2011). Two-Stage Monte Carlo Tree Search for Connect6. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 3
- Nozomu Ikehata, Takeshi Ito (2011). Monte-Carlo Tree Search In Ms. Pac-Man. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 3 [26]
- Junichi Hashimoto, Akihiro Kishimoto, Kazuki Yoshizoe, Kokolo Ikeda (2011). Accelerated UCT and Its Application to Two-Player Games. Advances in Computer Games 13
- Jan Stankiewicz, Mark Winands, Jos Uiterwijk (2011). Monte-Carlo Tree Search Enhancements for Havannah. Advances in Computer Games 13
- Gabriel Van Eyck, Martin Müller (2011). Revisiting Move Groups in Monte-Carlo Tree Search. Advances in Computer Games 13
- Hendrik Baier, Mark Winands (2011). Active Opening Book Application for Monte-Carlo Tree Search in 19x19 Go. BNAIC 2011, pdf
- Hendrik Baier, Mark Winands (2011). Time Management for Monte-Carlo Tree Search in Go. Advances in Computer Games 13
- Richard J. Lorentz (2011). An MCTS Program to Play EinStein Würfelt Nicht! Advances in Computer Games 13
- Cheng-Wei Chou, Ping-Chiang Chou, Hassen Doghmen, Chang-Shing Lee, Tsan-Cheng Su, Fabien Teytaud, Olivier Teytaud, Hui-Ming Wang, Mei-Hui Wang, Li-Wen Wu, Shi-Jim Yen (2011). Towards a Solution of 7x7 Go with Meta-MCTS. Advances in Computer Games 13
- Bruno Bouzy, Marc Métivier, Damien Pellier (2011). MCTS Experiments on the Voronoi Game. Advances in Computer Games 13
- Pim Nijssen, Mark Winands (2011). Playout Search for Monte-Carlo Tree Search in Multi-Player Games. Advances in Computer Games 13
- Jiao Wang, Shiyuan Li, Jitong Chen, Xin Wei, Huizhan Lv, Xinhe Xu (2011). 4*4-Pattern and Bayesian Learning in Monte-Carlo Go. Advances in Computer Games 13
- Jeff Rollason (2011). Mixing MCTS with Conventional Static Evaluation: Experiments and shortcuts en-route to full UCT. AI Factory, Winter 2011 » UCT, Evaluation
- Sylvain Gelly, David Silver (2011). Monte-Carlo tree search and rapid action value estimation in computer Go. Artificial Intelligence, Vol. 175, No. 11
- Lars Schaefers, Marco Platzner, Ulf Lorenz (2011). UCT-Treesplit - Parallel MCTS on Distributed Memory. MCTS Workshop, Freiburg, Germany, pdf
- Tobias Graf, Ulf Lorenz, Marco Platzner, Lars Schaefers (2011). Parallel Monte-Carlo Tree Search for HPC Systems. Euro-Par 2011, pdf
- Joel Veness, Marc Lanctot, Michael Bowling (2011). Variance Reduction in Monte-Carlo Tree Search. NIPS, pdf
- Joel Veness, Kee Siong Ng, Marcus Hutter, William Uther , David Silver (2011). A Monte-Carlo AIXI Approximation. JAIR, Vol. 40, pdf
- Christopher D. Rosin (2011). Nested Rollout Policy Adaptation for Monte Carlo Tree Search. IJCAI 2011, pdf
- David Tolpin, Solomon Eyal Shimony (2011). Doing Better Than UCT: Rational Monte Carlo Sampling in Trees. arXiv:1108.3711 » UCT
2012
- Michael L. Littman (2012). Technical Perspective: A New Way to Search Game Trees. Communications of the ACM, Vol. 55, No. 3
- Sylvain Gelly, Marc Schoenauer, Michèle Sebag, Olivier Teytaud, Levente Kocsis, David Silver, Csaba Szepesvári (2012). The Grand Challenge of Computer Go: Monte Carlo Tree Search and Extensions. Communications of the ACM, Vol. 55, No. 3, pdf preprint
- Oleg Arenz (2012). Monte Carlo Chess. B.Sc. thesis, Darmstadt University of Technology, advisor Johannes Fürnkranz, pdf » Stockfish
- Jeff Rollason (2012). Tuning Spades. AI Factory, Summer 2012 » UCT
- David Tolpin, Solomon Eyal Shimony (2012). MCTS Based on Simple Regret. AAAI-2012, arXiv:1207.5536
- David Tolpin, Solomon Eyal Shimony (2012). VOI-aware MCTS. ECAI 2012, arXiv:1207.5589 [27]
- Tristan Cazenave, Fabien Teytaud (2012). Beam Nested Rollout Policy Adaptation. ECAI CGW 2012
- André Fabbri, Frédéric Armetta, Eric Duchêne, Salima Hassas (2012). A new self-acquired knowledge process for Monte Carlo Tree Search. ECAI CGW 2012
- Marc Lanctot, Abdallah Saffidine, Joel Veness, Christopher Archibald (2012). Sparse Sampling for Adversarial Games. ECAI CGW 2012
- Niek Den Teuling, Mark Winands (2012). Monte-Carlo Tree Search for the Simultaneous Move Game Tron. ECAI CGW 2012, pdf
- Arthur Guez, David Silver, Peter Dayan (2012). Efficient Bayes-Adaptive Reinforcement Learning using Sample-Based Search. arXiv:1205.3109
- Truong-Huy Dinh Nguyen, Wee Sun Lee, Tze-Yun Leong (2012). Bootstrapping Monte Carlo Tree Search with an Imperfect Heuristic. arXiv:1206.5940
- Jan Kuipers, Aske Plaat, Jos Vermaseren, Jaap van den Herik (2012). Improving multivariate Horner schemes with Monte Carlo tree search. CoRR abs/1207.7079
- Cameron Browne, Edward Powley, Daniel Whitehouse, Simon Lucas, Peter Cowling, Philipp Rohlfshagen, Stephen Tavener, Diego Perez, Spyridon Samothrakis, Simon Colton (2012). A Survey of Monte Carlo Tree Search Methods. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 4, No. 1, pdf
- Pim Nijssen, Mark Winands (2012). Monte-Carlo Tree Search for the Hide-and-Seek Game Scotland Yard. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 4, No. 4 [28]
- Hendrik Baier, Mark Winands (2012). Nested Monte-Carlo Tree Search for Online Planning in Large MDPs. ECAI 2012, pdf
- Hendrik Baier, Mark Winands (2012). Beam Monte-Carlo Tree Search. IEEE CIG 2012, pdf
- Thomas Philip Runarsson, Marc Schoenauer, Michèle Sebag (2012). Pilot, Rollout and Monte Carlo Tree Search Methods for Job Shop Scheduling. arXiv:1210.0374
- Adrien Couetoux, Olivier Teytaud, Hassen Doghmen (2012). Learning a Move-Generator for Upper Confidence Trees. ICS 2012, Hualien
- Haruhiko Akiyama, Kanako Komiya, Yoshiyuki Kotani (2012). Nested Monte-Carlo Search with simulation reduction. Knowledge-Based Systems, Vol. 34 [29] [30]
2013
- Cheng-Wei Chou, Ping-Chiang Chou, Chang-Shing Lee, David L. Saint-Pierre, Olivier Teytaud, Mei-Hui Wang, Li-Wen Wu, Shi-Jim Yen (2013). Strategic Choices: Small Budgets and Simple Regret. TAAI 2012, Excellent Paper Award, pdf
- Daniel S. Abdi (2013). Monte carlo methods for estimating game tree size. pdf [31] » Perft
- Marc Lanctot (2013). Monte Carlo Sampling and Regret Minimization for Equilibrium Computation and Decision-Making in Large Extensive Form Games. Ph.D. thesis, University of Alberta, advisor Michael Bowling
- Aviezri Fraenkel (2013). Reflection. ICGA Journal, Vol. 36, No. 1 » Stanislaw Ulam
- Jeff Rollason (2013). Reducing the burden of knowledge: Simulation-based methods in imperfect information games. AI Factory, Summer 2013
- Abdallah Saffidine (2013). Solving Games and All That. Ph.D. thesis, 2.5 Monte Carlo Tree Search
- Shih-Chieh Huang, Martin Müller (2013). Investigating the Limits of Monte Carlo Tree Search Methods in Computer Go. CG 2013
- Shih-Chieh Huang, Broderick Arneson, Ryan Hayward, Martin Müller, Jakub Pawlewicz (2013). MoHex 2.0: a pattern-based MCTS Hex player. CG 2013, pdf
- Tobias Graf, Lars Schaefers, Marco Platzner (2013). On Semeai Detection in Monte-Carlo Go. CG 2013, pdf
- Richard J. Lorentz, Therese Horey (2013). Programming Breakthrough. CG 2013 » Breakthrough (Game)
- Ingo Althöfer, Wesley Turner (2013). Anomalies of Pure Monte Carlo Search in Monte Carlo Perfect Games. CG 2013
- Simon Viennot, Kokolo Ikeda (2013). Efficiency of Static Knowledge Bias in Monte-Carlo Tree Search. CG 2013
- Sumudo Fernando, Martin Müller (2013). Analyzing Simulations in Monte-Carlo Tree Search for the Game of Go. CG 2013
- Ingo Althöfer (2013). The wild Years are gone: Monte Carlo in Smoother Waters. Conference Report CG 2013, ICGA Journal, Vol. 36, No. 3
- Marc Lanctot, Abdallah Saffidine, Joel Veness, Christopher Archibald, Mark Winands (2013). Monte Carlo *-Minimax Search. IJCAI 2013
- Pim Nijssen (2013). Monte-Carlo Tree Search for Multi-Player Games. Ph.D. thesis, Maastricht University, pdf
- Jeff Rollason (2013). Searching the Unknown with MCTS. AI Factory, Winter 2013
- David Silver, Richard Sutton, Martin Mueller (2013). Temporal-Difference Search in Computer Go. ICAPS-13, pdf
- Hendrik Baier, Mark Winands (2013). Monte-Carlo Tree Search and minimax hybrids. CIG 2013, pdf
- Timothy Furtak, Michael Buro (2013). Recursive Monte Carlo search for imperfect information games. CIG 2013, pdf
- Ben Ruijl, Jos Vermaseren, Aske Plaat, Jaap van den Herik (2013). Combining Simulated Annealing and Monte Carlo Tree Search for Expression Simplification. CoRR abs/1312.0841
- Arthur Guez, David Silver, Peter Dayan (2013). Scalable and Efficient Bayes-Adaptive Reinforcement Learning Based on Monte-Carlo Tree Search. Journal of Artificial Intelligence Research, Vol. 48
- Ari Weinstein, Michael L. Littman, Sergiu Goschin (2013). Rollout-based Game-tree Search Outprunes Traditional Alpha-beta. PMLR, Vol. 24 » UCT
- Kuo-Yuan Kao, I-Chen Wu, Shi-Jim Yen, Yi-Chang Shan (2013). Incentive Learning in Monte Carlo Tree Search. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 5, No. 4
2014
- Ben Ruijl, Jos Vermaseren, Aske Plaat, Jaap van den Herik (2014). HEPGAME and the Simplification of Expressions. CoRR abs/1405.6369
- Marc Lanctot, Mark Winands, Tom Pepels, Nathan Sturtevant (2014). Monte Carlo Tree Search with Heuristic Evaluations using Implicit Minimax Backups. CIG 2014, arXiv:1406.0486
- S. Ali Mirsoleimani, Aske Plaat, Jaap van den Herik, Jos Vermaseren (2014). Performance analysis of a 240 thread tournament level MCTS Go program on the Intel Xeon Phi. CoRR abs/1409.4297 » Go, Parallel Search, x86-64
- Ben Ruijl, Jos Vermaseren, Aske Plaat, Jaap van den Herik (2014). Why Local Search Excels in Expression Simplification. CoRR abs/1409.5223
- Lars Schaefers (2014). Parallel Monte-Carlo Tree Search for HPC Systems and its Application to Computer Go. Ph.D. thesis, Paderborn University, advisors Marco Platzner, Ulf Lorenz, pdf, pdf
- Rémi Munos (2014). From Bandits to Monte-Carlo Tree Search: The Optimistic Principle Applied to Optimization and Planning. Foundations and Trends in Machine Learning, Vol. 7, No 1, hal-00747575v5, slides as pdf
- David W. King (2014). Complexity, Heuristic, and Search Analysis for the Games of Crossings and Epaminondas. Masters thesis, Air Force Institute of Technology, pdf [32]
- David W. King, Gilbert L. Peterson (2014). Epaminondas: Exploring Combat Tactics. ICGA Journal, Vol. 37, No. 3 [33]
- Ting-Fu Liao, I-Chen Wu, Guan-Wun Chen, Chung-Chin Shih, Po-Ya Kang, Bing-Tsung Chiang, Ting-Chu Ho, Ti-Rong Wu (2014). A Study of Software Framework for Parallel Monte Carlo Tree Search. GPW-2014
- Hendrik Baier, Mark Winands (2014). Monte-Carlo Tree Search and Minimax Hybrids with Heuristic Evaluation Functions. ECAI CGW 2014
- Nicolas Jouandeau, Tristan Cazenave (2014). Small and Large MCTS Playouts applied to Chinese Dark Chess Stochastic Game. ECAI CGW 2014
- Tom Pepels, Tristan Cazenave, Mark Winands, Marc Lanctot (2014). Minimizing Simple and Cumulative Regret in Monte-Carlo Tree Search. ECAI CGW 2014
- Denis Robilliard, Cyril Fonlupt, Fabien Teytaud (2014). Monte-Carlo Tree Search for the Game of “7 Wonders”. ECAI CGW 2014 [34]
- Nobuo Araki, Masakazu Muramatsu, Kunihito Hoki, Satoshi Takahashi (2014). Monte-Carlo Simulation Adjusting. AAAI-2014
- Johannes Heinrich, David Silver (2014). Self-Play Monte-Carlo Tree Search in Computer Poker. AAAI-2014
- Simon Lucas, Spyridon Samothrakis, Diego Perez (2014). Fast Evolutionary Adaptation for Monte Carlo Tree Search. EvoApplications 2014, pdf
2015 ...
- Richard J. Lorentz (2015). Early Playout Termination in MCTS. Advances in Computer Games 14
- Tristan Cazenave (2015). Playout Policy Adaptation for Games. Advances in Computer Games 14
- Tobias Graf, Marco Platzner (2015). Adaptive Playouts in Monte Carlo Tree Search with Policy Gradient Reinforcement Learning. Advances in Computer Games 14
- Chu-Hsuan Hsueh, I-Chen Wu, Wen-Jie Tseng, Shi-Jim Yen, Jr-Chang Chen (2015). Strength Improvement and Analysis for an MCTS-Based Chinese Dark Chess Program. Advances in Computer Games 14
- Yusaku Mandai, Tomoyuki Kaneko (2015). LinUCB Applied to Monte Carlo Tree Search. Advances in Computer Games 14
- Yun-Ching Liu, Yoshimasa Tsuruoka (2015). Adapting Improved Upper Confidence Bounds for Monte-Carlo Tree Search. Advances in Computer Games 14
- Jiao Wang, Tan Zhu, Hongye Li, Chu-Hsuan Hsueh, I-Chen Wu (2015). Belief-state Monte-Carlo tree search for Phantom games. IEEE CIG 2015
- Hung-Jui Chang, Chih-Wen Hsueh, Tsan-sheng Hsu (2015). Convergence and correctness analysis of Monte-Carlo tree search algorithms: A case study of 2 by 4 Chinese dark chess. IEEE CIG 2015
- Fabien Teytaud, Julien Dehos (2015). On the Tactical and Strategic Behaviour of MCTS when Biasing Random Simulations. ICGA Journal, Vol. 38, No. 2
- Jeff Rollason (2015). Mixing the Immiscible - MCTS and evaluation. AI Factory, October 2015 [35]
- S. Ali Mirsoleimani, Aske Plaat, Jaap van den Herik, Jos Vermaseren (2015). Scaling Monte Carlo Tree Search on Intel Xeon Phi. CoRR abs/1507.04383 » Hex, Parallel Search, x86-64
- S. Ali Mirsoleimani, Aske Plaat, Jaap van den Herik, Jos Vermaseren (2015). Parallel Monte Carlo Tree Search from Multi-core to Many-core Processors. TrustCom/BigDataSE/ISPA 2015, pdf
- Peter H. Jin, Kurt Keutzer (2015). Convolutional Monte Carlo Rollouts in Go. arXiv:1512.03375
- Naoki Mizukami, Yoshimasa Tsuruoka (2015). Building a Computer Mahjong Player Based on Monte Carlo Simulation and Opponent Models. IEEE CIG 2015, pdf
- Hendrik Baier (2015). Monte-Carlo Tree Search Enhancements for One-Player and Two-Player Domains. Ph.D. thesis, Maastricht University, pdf [36]
- Lars Schaefers, Marco Platzner (2015). Distributed Monte Carlo Tree Search: A Novel Technique and its Application to Computer Go. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 7, No. 4 [37]
- Bojun Huang (2015). Pruning Game Tree by Rollouts. AAAI » MT-SSS* [38]
2016
- David Silver, Aja Huang, Chris J. Maddison, Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, Sander Dieleman, Dominik Grewe, John Nham, Nal Kalchbrenner, Ilya Sutskever, Timothy Lillicrap, Madeleine Leach, Koray Kavukcuoglu, Thore Graepel, Demis Hassabis (2016). Mastering the game of Go with deep neural networks and tree search. Nature, Vol. 529 » AlphaGo
- Tobias Graf, Marco Platzner (2016). Using Deep Convolutional Neural Networks in Monte Carlo Tree Search. CG 2016
- Takahisa Imagawa, Tomoyuki Kaneko (2016). Monte Carlo Tree Search with Robust Exploration. CG 2016
- Joris Duguépéroux, Ahmad Mazyad, Fabien Teytaud, Julien Dehos (2016). Pruning playouts in Monte-Carlo Tree Search for the game of Havannah. CG 2016
- Peter H. Jin, Kurt Keutzer (2016). Convolutional Monte Carlo Rollouts for Computer Go. CG 2016
- Hendrik Baier, Mark Winands (2016). Time Management for Monte Carlo Tree Search. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 8, No. 3
- Katsuki Ohto, Tetsuro Tanaka (2016). Application of Monte Carlo Tree Search to Curling AI. 21st Game Programming Workshop
- Maciej Świechowski, Jacek Mańdziuk (2016). A Hybrid Approach to Parallelization of Monte Carlo Tree Search in General Game Playing. Challenging Problems and Solutions in Intelligent Systems, Springer
- S. Ali Mirsoleimani, Aske Plaat, Jaap van den Herik, Jos Vermaseren (2016). A New Method for Parallel Monte Carlo Tree Search. arXiv:1605.04447 » Parallel Search
- S. Ali Mirsoleimani, Aske Plaat, Jaap van den Herik, Jos Vermaseren (2016). An Efficient Computation Pattern for Parallel MCTS. ICT.OPEN 2016, pdf
- David L. St-Pierre, Jean-Baptiste Hoock, Jialin Liu, Fabien Teytaud, Olivier Teytaud (2016). Automatically Reinforcing a Game AI. arXiv:1607.0810
- Tristan Cazenave, Abdallah Saffidine, Michael Schofield, Michael Thielscher (2016). Nested Monte Carlo Search for Two-Player Games. AAAI 2016, pdf
2017
- Dap Hartmann (2017). Let's Catch the Train to Monte-Carlo. ICGA Journal, Vol. 39, No. 1, Review on Hendrik Baier's Ph.D. thesis
- S. Ali Mirsoleimani, Aske Plaat, Jaap van den Herik, Jos Vermaseren (2017). Structured Parallel Programming for Monte Carlo Tree Search. arXiv:1704.00325
- S. Ali Mirsoleimani, Aske Plaat, Jaap van den Herik, Jos Vermaseren (2017). An Analysis of Virtual Loss in Parallel MCTS. ICAART 2017, Vol. 2, pdf
- Katsuki Ohto, Tetsuro Tanaka (2017). A Curling Agent Based on the Monte-Carlo Tree Search Considering the Similarity of the Best Action among Similar States. Advances in Computer Games 15
- Naoki Mizukami, Jun Suzuki, Hirotaka Kameko, Yoshimasa Tsuruoka (2017). Exploration Bonuses Based on Upper Confidence Bounds for Sparse Reward Games. Advances in Computer Games 15
- David Silver, Thomas Hubert, Julian Schrittwieser, Ioannis Antonoglou, Matthew Lai, Arthur Guez, Marc Lanctot, Laurent Sifre, Dharshan Kumaran, Thore Graepel, Timothy Lillicrap, Karen Simonyan, Demis Hassabis (2017). Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. arXiv:1712.01815 » AlphaZero
- Shantanu Thakoor, Surag Nair, Megha Jhunjhunwala (2017). Learning to Play Othello Without Human Knowledge. Stanford University, pdf » AlphaZero, Othello, Deep Learning [39]
- Hendrik Baier (2017). A Rollout-Based Search Algorithm Unifying MCTS and Alpha-Beta. Computer Games » Rollout Paradigm
- Tristan Cazenave (2017). Nested Rollout Policy Adaptation with Selective Policies. Computer Games
- Nobuo Araki, Kunihito Hoki, Satoshi Takahashi, Masakazu Muramatsu (2017). Improved simulation adjusting. ICGA Journal, Vol. 39, Nos. 3-4
2018
- Arthur Guez, Théophane Weber, Ioannis Antonoglou, Karen Simonyan, Oriol Vinyals, Daan Wierstra, Rémi Munos, David Silver (2018). Learning to Search with MCTSnets. arXiv:1802.04697
- Hui Wang, Michael Emmerich, Aske Plaat (2018). Monte Carlo Q-learning for General Game Playing. arXiv:1802.05944 » Reinforcement Learning, General Game Playing
- Mark Winands (2018). The Magic of Monte-Carlo Tree Search. AI Factory, January 2018
- Jacek Mańdziuk (2018). MCTS/UCT in Solving Real-Life Problems. Advances in Data Analysis with Computational Intelligence Methods, Springer
- Karol Walędzik, Jacek Mańdziuk (2018). Applying Hybrid Monte Carlo Tree Search Methods to Risk-Aware Project Scheduling Problem. Information Sciences, Vol. 460
- Chenjun Xiao, Jincheng Mei, Martin Müller (2018). Memory-Augmented Monte Carlo Tree Search. AAAI 2018
- Chao Gao, Martin Müller, Ryan Hayward (2018). Three-Head Neural Network Architecture for Monte Carlo Tree Search. IJCAI 2018
- Tobias Joppen, Christian Wirth, Johannes Fürnkranz (2018). Preference-Based Monte Carlo Tree Search. arXiv:1807.06286
- Seydou Ba, Takuya Hiraoka, Takashi Onishi, Toru Nakata, Yoshimasa Tsuruoka (2018). Monte Carlo Tree Search with Scalable Simulation Periods for Continuously Running Tasks. arXiv:1809.02378
- S. Ali Mirsoleimani, Jaap van den Herik, Aske Plaat, Jos Vermaseren (2018). Pipeline Pattern for Parallel MCTS. ICAART 2018, pdf
- S. Ali Mirsoleimani, Jaap van den Herik, Aske Plaat, Jos Vermaseren (2018). A Lock-free Algorithm for Parallel MCTS. ICAART 2018, pdf
- Ching-Nung Lin, Jr-Chang Chen, Shi-Jim Yen, Chan-San Chen (2018). Design of a Block Go program using deep learning and Monte Carlo tree search. ICGA Journal, Vol. 40, No. 3
- Kiminori Matsuzaki, Naoki Kitamura (2018). Do evaluation functions really improve Monte-Carlo tree search? CG 2018, ICGA Journal, Vol. 40, No. 3
- Shun-Shii Lin, Chih-Hung Chen, Yu-Heng Chen, Wei-Lin Wu (2018). Some improvements in Monte Carlo tree search algorithms for sudden death games. CG 2018, ICGA Journal, Vol. 40, No. 4
- Nai-Yuan Chang, Chih-Hung Chen, Shun-Shii Lin, Surag Nair (2018). The Big Win Strategy on Multi-Value Network: An Improvement over AlphaZero Approach for 6x6 Othello. MLMI2018
- Yen-Chi Chen, Chih-Hung Chen, Shun-Shii Lin (2018). Exact-Win Strategy for Overcoming AlphaZero. CIIS 2018 [40]
2019
- Tobias Joppen, Johannes Fürnkranz (2019). Ordinal Monte Carlo Tree Search. TU Darmstadt, arXiv:1901.04274
- Herilalaina Rakotoarison, Marc Schoenauer, Michèle Sebag (2019). Automated Machine Learning with Monte-Carlo Tree Search. arXiv:1906.00170
- Aline Hufschmitt, Jean-Noël Vittaut, Nicolas Jouandeau (2019). Exploiting Game Decompositions in Monte Carlo Tree Search. Advances in Computer Games 16
2020 ...
- Johannes Czech, Patrick Korus, Kristian Kersting (2020). Monte-Carlo Graph Search for AlphaZero. arXiv:2012.11045 » AlphaZero, CrazyAra
- Quentin Cohen-Solal, Tristan Cazenave (2020). Minimax Strikes Back. arXiv:2012.10700
- Johannes Czech, Patrick Korus, Kristian Kersting (2021). Improving AlphaZero Using Monte-Carlo Graph Search. Proceedings of the Thirty-First International Conference on Automated Planning and Scheduling, Vol. 31, pdf
- Maximilian Langer (2021). Evaluation of Monte-Carlo Tree Search for Xiangqi. B.Sc. thesis, TU Darmstadt, pdf » Xiangqi
Forum Posts
2010 ...
- [Computer-go] learning patterns for mc go by Hendrik Baier, Computer Go Archive, April 26, 2010
- UCT surprise for checkers ! by Daniel Shawul, CCC, March 25, 2011
- MCTS without random playout? by Antonio Torrecillas, CCC, January 01, 2012 » B*
- Re: MC methods by Daniel Shawul, CCC, April 13, 2013 » Perft
2015 ...
- monte carlo tree search question by Marco Belli, CCC, January 31, 2016
- The scaling of Deep Learning MCTS Go engines by Kai Laskos, CCC, October 23, 2016 » Deep Learning, Go
2017
- A branch to test the Monte Carlo algorithm in Stockfish by Stephane Nicolet, FishCooking, December 06, 2017 » Stockfish, AlphaZero
- Nebiyu-MCTS vs TSCP 1-0 by Daniel Shawul, CCC, December 10, 2017 » Nebiyu
- An AlphaZero inspired project by Truls Edvard Stokke, CCC, December 14, 2017 » AlphaZero
- MCTS wrapper for StockFish by Jonathan Baxter, FishCooking, December 19, 2017 » Stockfish
- Search traps in MCTS and chess by Daniel Shawul, CCC, December 25, 2017 » Sampling-Based Planning
- MCTS weakness wrt AB (via Daniel Shawul) by Chris Whittington, Rybka Forum, December 25, 2017
2018
- Alpha-Beta as a rollouts algorithm by Daniel Shawul, CCC, January 25, 2018 » Alpha-Beta, MCαβ, Scorpio
- comparing minimax and averaging MCTS with alphabeta rollouts by Daniel Shawul, CCC, March 20, 2018 » Scorpio
- MCTS beginner questions by Martin Fierz, CCC, April 25, 2018
- MCTS with minmax backup operator? by Martin Fierz, CCC, May 01, 2018
- Komodo 12 and MCTS by Larry Kaufman, CCC, May 14, 2018 » Komodo
2019
- MCTS: How to deal with extreme imbalances by Alexandru Mosoi, CCC, January 16, 2019 » Zurichess
- MCTS implementation question by mobmat, CCC, February 22, 2019 [41]
- Training the trainer: how is it done for Stockfish? by Marc-Philippe Huget, CCC, March 01, 2019 » Stockfish
- Re: Training the trainer: how is it done for Stockfish? by Graham Jones, CCC, March 03, 2019 » Leela Chess Zero
- Training using 1 playout instead of 800 by Daniel Shawul, CCC, April 26, 2019
- Re: On-line engine blitz tourney April by Rémi Coulom, CCC, April 27, 2019
- Question to Remi about CrazyZero by Harm Geert Muller, CCC, April 28, 2019 » CrazyZero
- SL vs RL by Chris Whittington, CCC, April 28, 2019
- How to get the "usual" Multi PV with MCTS engines? by Kai Laskos, CCC, May 21, 2019 » MultiPV
- A question to MCTS + NN experts by Maksim Korzh, CCC, July 17, 2019 » Deep Learning
- Re: A question to MCTS + NN experts by Daniel Shawul, CCC, July 17, 2019
2020 ...
- MCTS evaluation question by Maksim Korzh, CCC, November 02, 2020
- Re: Has CrazyAra really improved because of MTGS ? by Johannes Czech, CCC, July 08, 2021 » CrazyAra
External Links
Monte Carlo Tree Search
- Monte Carlo tree search from Wikipedia
- Monte Carlo Tree Search - beginners guide int8.io [42]
- Sensei's Library: Monte Carlo Tree Search
- Sensei's Library: UCT
- Lange Nacht der Wissenschaften - Long Night of Sciences Jena - 2007 by Ingo Althöfer, MC and UCT poster by Jakob Erdmann
- A Simple Alpha(Go) Zero Tutorial by Surag Nair, Stanford University, December 29, 2017 » AlphaZero, Deep Learning
- Monte Carlo Tree Search by John Levine, University of Strathclyde, March 05, 2017, YouTube Video
- Monte Carlo instead of Alpha-Beta? by Stephan Oliver Platz, ChessBase News, January 30, 2019 » Komodo MCTS
Monte Carlo Misc
- Rybka's Monte Carlo analysis by Steve Lopez, ChessBase News, February 03, 2009 » Rybka
- Monte Carlo (disambiguation) from Wikipedia
- A History of Monte Carlo
- Software Development in the UNIX Environment - Example C Program to Compute PI Using A Monte Carlo Method
- Calculation of Pi Using the Monte Carlo Method by Eve Astrid Andersson
- Slot machine from Wikipedia
- Monte-Carlo Simulation Balancing - videolectures.net by David Silver [43]
- Marcus Miller - State of Mind (Raúl Midón), A Night In Monte-Carlo (2010), YouTube Video
- feat. Raúl Midón, Roy Hargrove and the Monte-Carlo Philharmonic Orchestra, November 29, 2008, Monte-Carlo Jazz Festival
References
- ↑ Edvard Munch, At the Roulette Table in Monte Carlo, 1893, Edvard Munch from Wikipedia
- ↑ Rémi Coulom (2009). The Monte-Carlo Revolution in Go. JFFoS'2008: Japanese-French Frontiers of Science Symposium, slides as pdf
- ↑ Julien Kloetzer, Hiroyuki Iida, Bruno Bouzy (2007). The Monte-Carlo approach in Amazons. CGW 2007
- ↑ Richard J. Lorentz (2008). Amazons Discover Monte-Carlo. CG 2008
- ↑ Mark Winands, Yngvi Björnsson (2009). Evaluation Function Based Monte-Carlo LOA. pdf
- ↑ Richard J. Lorentz (2010). Improving Monte-Carlo Tree Search in Havannah. CG 2010
- ↑ Broderick Arneson, Ryan Hayward, Philip Henderson (2010). Monte Carlo Tree Search in Hex. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 2, No. 4, pdf
- ↑ UCT surprise for checkers ! by Daniel Shawul, CCC, March 25, 2011
- ↑ David Silver, Thomas Hubert, Julian Schrittwieser, Ioannis Antonoglou, Matthew Lai, Arthur Guez, Marc Lanctot, Laurent Sifre, Dharshan Kumaran, Thore Graepel, Timothy Lillicrap, Karen Simonyan, Demis Hassabis (2017). Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. arXiv:1712.01815
- ↑ Raghuram Ramanujan, Ashish Sabharwal, Bart Selman (2010). On Adversarial Search Spaces and Sampling-Based Planning. ICAPS 2010
- ↑ Oleg Arenz (2012). Monte Carlo Chess. B.Sc. thesis, Darmstadt University of Technology, advisor Johannes Fürnkranz, pdf
- ↑ Guillaume Chaslot, Mark Winands, Jaap van den Herik (2008). Parallel Monte-Carlo Tree Search. CG 2008, pdf
- ↑ Guillaume Chaslot, Mark Winands, Jaap van den Herik (2008). Parallel Monte-Carlo Tree Search. CG 2008, pdf
- ↑ Steps of Monte-Carlo Tree Search by Mciura, March 31, 2013, Wikimedia Commons, Monte Carlo tree search from Wikipedia
- ↑ Ingo Althöfer (2011). On Board-Filling Games with Random-Turn Order and Monte Carlo Perfectness. Advances in Computer Games 13
- ↑ Levente Kocsis, Csaba Szepesvári (2006). Bandit based Monte-Carlo Planning ECML-06, LNCS/LNAI 4212, pp. 282-293. introducing UCT, pdf
- ↑ Christopher D. Rosin (2011). Multi-armed bandits with episode context. Annals of Mathematics and Artificial Intelligence, Vol. 61, No. 3, ISAIM 2010 pdf
- ↑ Quentin Cohen-Solal, Tristan Cazenave (2020). Minimax Strikes Back. arXiv:2012.10700
- ↑ Morpion solitaire from Wikipedia
- ↑ Jeff Rollason (2015). Mixing the Immiscible - MCTS and evaluation. AI Factory, October 2015
- ↑ Monte Carlo in LOA by Mark Watkins, Open Chess Forum, December 30, 2010
- ↑ The Settlers of Catan from Wikipedia
- ↑ Blokus Duo from Wikipedia
- ↑ Search traps in MCTS and chess by Daniel Shawul, CCC, December 25, 2017
- ↑ NoGo (ICGA Tournaments)
- ↑ Ms. Pac-Man from Wikipedia
- ↑ Value of information (VOI) from Wikipedia
- ↑ Scotland Yard (board game) from Wikipedia
- ↑ Morpion solitaire from Wikipedia
- ↑ Morpion Solitaire - Record Grids (5T game)
- ↑ Re: MC methods by Daniel Shawul, CCC, April 13, 2013
- ↑ Crossings from Wikipedia
- ↑ Epaminondas from Wikipedia
- ↑ 7 Wonders (board game) from WIkipedia
- ↑ Guillaume Chaslot, Mark Winands, Jos Uiterwijk, Jaap van den Herik, Bruno Bouzy (2008). Progressive Strategies for Monte-Carlo Tree Search. New Mathematics and Natural Computation, Vol. 4, No. 3, pdf
- ↑ Dap Hartmann (2017). Let's Catch the Train to Monte-Carlo. ICGA Journal, Vol. 39, No. 1
- ↑ Re: Minmax backup operator for MCTS by Brahim Hamadicharef, CCC, December 30, 2017
- ↑ Re: Announcing lczero by Daniel Shawul, CCC, January 21, 2018 » Leela Chess Zero
- ↑ GitHub - suragnair/alpha-zero-general: A clean and simple implementation of a self-play learning algorithm based on AlphaGo Zero (any game, any framework!)
- ↑ "Exact-Win Strategy for Overcoming AlphaZero" · Issue #799 · LeelaChessZero/lc0 · GitHub
- ↑ GitHub - dkappe/leela_lite: A toolkit for experimenting with UCT and Leela Chess nets in Python by Dietrich Kappe
- ↑ Re: MCTS evaluation question by Joerg Oster, CCC, November 03, 2020
- ↑ David Silver, Gerald Tesauro (2009). Monte-Carlo Simulation Balancing. ICML 2009, pdf