Home * Search * Principal Variation

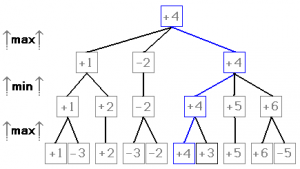
Variation (game tree), PV of a Minimax tree in blue ^[1]

The Principal variation (PV) is a sequence of moves that programs consider best and therefore expect to be played. All the nodes included by the PV are PV-nodes. Inside an iterative deepening framework, it is the most important move ordering consideration to play the PV collected during the current iteration, as the very first left moves of the next iteration. Although not needed for pure chess playing, most engines print the Principal Variation every time it changes or a new depth is reached for analyzing purposes. There are several implementations to determine the PV - most notably the three mentioned below, which were often controversial discussed in Computer Chess Forums with all their pros and contras ^[2] ^[3] .

Transposition Table

The best moves from the exact entries of the Transposition table may reveal the PV without (much) extra effort.

Pro: implementation without extra effort
Contra: dependent on the replacement scheme, TT-overwrites may shorten the PV

Collection during search

PV-Tables (or Refutation Tables) are used to collect and propagate best moves and the PV up to the root similar to the best score.

Pro: easy implementation; does not risk the cut PV lines in case of PV overwrites
Contra: slows down search a little; PV might be cut in case of TT-cutoffs

Triangular PV-Table

A Triangular PV-Table is the most dense implementation of a pre-allocated PV-Table, taking into account that the farther the root the shorter the maximal PVs along the maximum search depth. The space advantage requires a more complicated index scheme though.

PV-List on the Stack

A simple implementation with a linked PV-List on the stack is described on Bruce Moreland's Computer Chess Pages ^[4] :

typedef struct LINE {
    int cmove;              // Number of moves in the line.
    MOVE argmove[moveMAX];  // The line.
}   LINE;

int AlphaBeta(int depth, int alpha, int beta, LINE * pline) {

    LINE line;
    if (depth == 0) {
        pline->cmove = 0;
        return Evaluate();
    }
    GenerateLegalMoves();
    while (MovesLeft()) {

        MakeNextMove();
        val = -AlphaBeta(depth - 1, -beta, -alpha, &line);
        UnmakeMove();

        if (val >= beta) return beta;
        if (val > alpha) {
            alpha = val;
            pline->argmove[0] = ThisMove();
            memcpy(pline->argmove + 1, line.argmove, line.cmove * sizeof(MOVE));
            pline->cmove = line.cmove + 1;
        }
    }
    return alpha;
}

LINE (a buffer that holds the PV) is created at the beginning of every node and a pointer to it is passed to every child nodes. If one of those raise alpha (become a new PV node) they copy their own PV - which is created in the same way as described now - into the pointer received from their parent node. Iteratively this returns the whole Principal Variation. Generally memcpy ^[5] is an expensive instruction but as alpha is raised only very rarely this does not harm performance too much. The main downside is the allocation of the struct LINE every node which might be dangerous for deep searches with a small stack available.

Separate PV TT

No matter how the PV is determined, the issue of short principal variations due to exact score hits with sufficient draft from the Transposition table at PV-nodes is one reason, why many programs ignore those matches and continue searching that node. Despite the search overhead seems tiny, since PV-nodes are rare, even more with exact hits, there are other solutions to address the short PV problem, which looses the information of the path that leads to that score, in conjunction with a more difficult debugging task.

Programs like Glass use a separate transposition table exclusively for PV-nodes - however similar results may be achieved with TT multi-tiers or bucket systems and replacement schemes taking care of exact scores of stored PV-nodes. Robert Hyatt had the idea to take the 64 bit hash signature, squash it to something relatively small like 12-16 bits and use that as an index into a PV-holder table ^[6] ^[7] ^[8] ^[9]. As an alternative, Steven Edwards proposed a structure of binary trees to recover the PV without any danger of overwriting causing a loss of information ^[10].

Pro: almost always full length PV returned
Contra: may slow down the search a little and has some space requirement

Multiple PVs

Multiple PVs, that is collecting not only one PV of the best move and testing others don't improve alpha, but collecting and reporting multiple PVs of one or more next best moves for analyzing purposes, requires a less efficient root search, where subsequent moves are searched with a wider alpha-beta window.

Publications

Selim Akl, Monroe Newborn (1977). The Principal Continuation and the Killer Heuristic. 1977 ACM Annual Conference Proceedings, pp. 466-473. ACM, Seattle, WA.
Robert Hyatt (2014). A Solution to Short PVs Caused by Exact Hash Matches. ICGA Journal, Vol. 37, No. 3 » Separate TT for the PV