Neural Networks
Home * Learning * Neural Networks

Neural Networks,
a series of connected neurons which communicate due to neurotransmission. The interface through which neurons interact with their neighbors consists of axon terminals connected via synapses to dendrites on other neurons. If the sum of the input signals into one neuron surpasses a certain threshold, the neuron sends an action potential at the axon hillock and transmits this electrical signal along the axon.
In 1949, Donald O. Hebb introduced his theory in The Organization of Behavior, stating that learning is about to adapt weight vectors (persistent synaptic plasticity) of the neuron pre-synaptic inputs, whose dot-product activates or controls the post-synaptic output, which is the base of Neural network learning [2].
Contents
AN
Already in the early 40s, Warren S. McCulloch and Walter Pitts introduced the artificial neuron as a logical element with multiple analogue inputs and a single digital output with a boolean result. The output fired "true", if the sum of the inputs exceed a threshold. In their 1943 paper A Logical Calculus of the Ideas Immanent in Nervous Activity [3], they attempted to demonstrate that a Turing machine program could be implemented in a finite network of such neurons of combinatorial logic functions of AND, OR and NOT.
ANNs
Artificial Neural Networks (ANNs) are a family of statistical learning devices or algorithms used in regression, and binary or multiclass classification, implemented in hardware or software inspired by their biological counterparts. The artificial neurons of one or more layers receive one or more inputs (representing dendrites), and after being weighted, sum them to produce an output (representing a neuron's axon). The sum is passed through a nonlinear function known as an activation function or transfer function. The transfer functions usually have a sigmoid shape, but they may also take the form of other non-linear functions, piecewise linear functions, or step functions [4]. The weights of the inputs of each layer are tuned to minimize a cost or loss function, which is a task in mathematical optimization and machine learning.
Perceptron

The perceptron is an algorithm for supervised learning of binary classifiers. It was the first artificial neural network, introduced in 1957 by Frank Rosenblatt [6], implemented in custom hardware. In its basic form it consists of a single neuron with multiple inputs and associated weights.
Supervised learning is applied using a set D of labeled training data with pairs of feature vectors (x) and given results as desired output (d), usually started with cleared or randomly initialized weight vector w. The output is calculated by all inputs of a sample, multiplied by its corresponding weights, passing the sum to the activation function f. The difference of desired and actual value is then immediately used modify the weights for all features using a learning rate 0.0 < α <= 1.0:
for (j=0, Σ = 0.0; j < nSamples; ++j) {
for (i=0, X = bias; i < nFeatures; ++i)
X += w[i]*x[j][i];
y = f ( X );
Σ += abs(Δ = d[j] - y);
for (i=0; i < nFeatures; ++i)
w[i] += α*Δ*x[j][i];
}
AI Winter

Although the perceptron initially seemed promising, it was proved that perceptrons could not be trained to recognise many classes of patterns. This led to neural network research stagnating for many years, the AI-winter, before it was recognised that a feedforward neural network with two or more layers had far greater processing power than with one layer. Single layer perceptrons are only capable of learning linearly separable patterns. In their 1969 book Perceptrons, Marvin Minsky and Seymour Papert wrote that it was impossible for these classes of network to learn the XOR function. It is often believed that they also conjectured (incorrectly) that a similar result would hold for a multilayer perceptron [8]. However, this is not true, as both Minsky and Papert already knew that multilayer perceptrons were capable of producing an XOR function [9]-
Backpropagation
In 1974, Paul Werbos started to end the AI winter concerning neural networks, when he first described the mathematical process of training multilayer perceptrons through backpropagation of errors [10], derived in the context of control theory by Henry J. Kelley in 1960 [11] and by Arthur E. Bryson in 1961 [12] using principles of dynamic programming, simplified by Stuart E. Dreyfus in 1961 applying the chain rule [13]. It was in 1982, when Werbos applied a automatic differentiation method described in 1970 by Seppo Linnainmaa [14] to neural networks in the way that is widely used today [15] [16] [17] [18].
Backpropagation is a generalization of the delta rule to multilayered feedforward networks, made possible by using the chain rule to iteratively compute gradients for each layer. Backpropagation requires that the activation function used by the artificial neurons be differentiable, which is true for the common sigmoid logistic function or its softmax generalization in multiclass classification.
Along with an optimization method such as gradient descent, it calculates the gradient of a cost or loss function with respect to all the weights in the neural network. The gradient is fed to the optimization method which in turn uses it to update the weights, in an attempt to minimize the loss function, which choice depends on the learning type (supervised, unsupervised, reinforcement) and the activation function - mean squared error or cross-entropy error function are used in binary classification [19]. The gradient is almost always used in a simple stochastic gradient descent algorithm. In 1983, Yurii Nesterov contributed an accelerated version of gradient descent that converges considerably faster than ordinary gradient descent [20] [21] [22] [23].
Backpropagation algorithm for a 3-layer network [24]:
initialize the weights in the network (often small random values)
do
for each example e in the training set
O = neural-net-output(network, e) // forward pass
T = teacher output for e
compute error (T - O) at the output units
compute delta_wh for all weights from hidden layer to output layer // backward pass
compute delta_wi for all weights from input layer to hidden layer // backward pass continued
update the weights in the network
until all examples classified correctly or stopping criterion satisfied
return the network
Deep Learning
Deep learning has been characterized as a buzzword, or a rebranding of neural networks. A deep neural network (DNN) is an ANN with multiple hidden layers of units between the input and output layers which can be discriminatively trained with the standard backpropagation algorithm. Two common issues if naively trained are overfitting and computation time.
Convolutional NNs
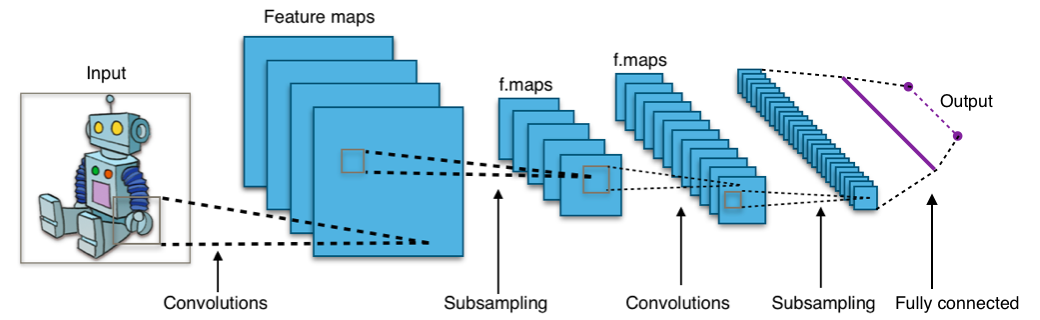
Convolutional neural networks (CNN) form a subclass of feedforward neural networks that have special weight constraints, individual neurons are tiled in such a way that they respond to overlapping regions. A neuron of a convolutional layer is connected to a correspondent receptive field of the previous layer, a small subset of their neurons. A distinguishing feature of CNNs is that many neurons share the same bias and vector of weights, dubbed filter. This reduces memory footprint because a single bias and a single vector of weights is used across all receptive fields sharing that filter, rather than each receptive field having its own bias and vector of weights. Convolutional NNs are suited for deep learning and are highly suitable for parallelization on GPUs [25]. They were research topic in the game of Go since 2008 [26], and along with the residual modification successful applied in Go and other games, most spectacular due to AlphaGo in 2015 and AlphaZero in 2017.
Typical CNN [27]
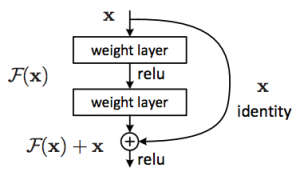
Residual Net
A Residual net (ResNet) adds the input of a layer, typically composed of a convolutional layer and of a ReLU layer, to its output. This modification, like convolutional nets inspired from image classification, enables faster training and deeper networks [30] [31] [32].
ANNs in Games
Applications of neural networks in computer games and chess are learning of evaluation and search control. Evaluation topics include feature selection and automated tuning, search control move ordering, selectivity and time management. The perceptron looks like the ideal learning algorithm for automated evaluation tuning.
Backgammon
In the late 80s, Gerald Tesauro pioneered in applying ANNs to the game of Backgammon. His program Neurogammon won the Gold medal at the 1st Computer Olympiad 1989 - and was further improved by TD-Lambda based Temporal Difference Learning within TD-Gammon [33]. Today all strong backgammon programs rely on heavily trained neural networks.
Go
In 2014, two teams independently investigated whether deep convolutional neural networks could be used to directly represent and learn a move evaluation function for the game of Go. Christopher Clark and Amos Storkey trained an 8-layer convolutional neural network by supervised learning from a database of human professional games, which without any search, defeated the traditional search program Gnu Go in 86% of the games [34] [35] [36] [37]. In their paper Move Evaluation in Go Using Deep Convolutional Neural Networks [38], Chris J. Maddison, Aja Huang, Ilya Sutskever, and David Silver report they trained a large 12-layer convolutional neural network in a similar way, to beat Gnu Go in 97% of the games, and matched the performance of a state-of-the-art Monte-Carlo Tree Search that simulates a million positions per move [39].
In 2015, a team affiliated with Google DeepMind around David Silver and Aja Huang, supported by Google researchers John Nham and Ilya Sutskever, build a Go playing program dubbed AlphaGo [40], combining Monte-Carlo tree search with their 12-layer networks [41].
Chess
Logistic regression as applied in Texel's Tuning Method may be interpreted as supervised learning application of the single-layer perceptron with one neuron. This is also true for reinforcement learning approaches, such as TD-Leaf in KnightCap or Meep's TreeStrap, where the evaluation consists of a weighted linear combination of features. Despite these similarities with the perceptron, these engines are not considered using ANNs - since they use manually selected chess specific feature construction concepts like material, piece square tables, pawn structure, mobility etc..
More sophisticated attempts to replace static evaluation by neural networks and perceptrons feeding in more unaffiliated feature sets like board representation and attack tables etc., where not yet that successful like in other games. Chess evaluation seems not that well suited for neural nets, but there are also aspects of too weak models and feature recognizers as addressed by Gian-Carlo Pascutto with Stoofvlees [42], huge training effort, and weak floating point performance - but there is still hope due to progress in hardware and parallelization using SIMD instructions and GPUs, and deeper and more powerful neural network structures and methods successful in other domains. In December 2017, Google DeepMind published about their generalized AlphaZero algorithm.
Move Ordering
Concerning move ordering - there were interesting NN proposals like the Chessmaps Heuristic by Kieran Greer et al. [43], and the Neural MoveMap Heuristic by Levente Kocsis et al. [44].
Giraffe & Zurichess
In 2015, Matthew Lai trained Giraffe's deep neural network by TD-Leaf [45]. Zurichess by Alexandru Moșoi uses the TensorFlow library for automated tuning - in a two layers neural network, the second layer is responsible for a tapered eval to phase endgame and middlegame scores [46].
DeepChess
In 2016, Omid E. David, Nathan S. Netanyahu, and Lior Wolf introduced DeepChess obtaining a grandmaster-level chess playing performance using a learning method incorporating two deep neural networks, which are trained using a combination of unsupervised pretraining and supervised training. The unsupervised training extracts high level features from a given chess position, and the supervised training learns to compare two chess positions to select the more favorable one. In order to use DeepChess inside a chess program, a novel version of alpha-beta is used that does not require bounds but positions αpos and βpos [47].
Alpha Zero
In December 2017, the Google DeepMind team along with former Giraffe author Matthew Lai reported on their generalized AlphaZero algorithm, combining Deep learning with Monte-Carlo Tree Search. AlphaZero can achieve, tabula rasa, superhuman performance in many challenging domains with some training effort. Starting from random play, and given no domain knowledge except the game rules, AlphaZero achieved a superhuman level of play in the games of chess and Shogi as well as Go, and convincingly defeated a world-champion program in each case [48]. The open souece projects Leela Zero (Go) and its chess adaptation Leela Chess Zero successfully re-implemented the ideas of DeepMind.
NNUE
NNUE reverse of ƎUИИ - Efficiently Updatable Neural Networks, is an NN architecture intended to replace the evaluation of Shogi, chess and other board game playing alpha-beta searchers. NNUE was introduced in 2018 by Yu Nasu [49], and was used in Shogi adaptations of Stockfish such as YaneuraOu [50] , and Kristallweizen [51], apparently with AlphaZero strength [52]. Nodchip incorporated NNUE into the chess playing Stockfish 10 as a proof of concept [53], yielding in the hype about Stockfish NNUE in summer 2020 [54]. Its heavily over parametrized computational most expensive input layer is efficiently incremental updated in make and unmake move.
NN Chess Programs
See also
- Cognition
- Deep Learning
- DeepChess
- Genetic Programming
- Memory
- Neural MoveMap Heuristic
- NNUE
- Pattern Recognition
- SANE
- Temporal Difference Learning
Selected Publications
1940 ...
- Walter Pitts (1942). Some observations on the simple neuron circuit. Bulletin of Mathematical Biology, Vol. 4, No. 3
- Warren S. McCulloch, Walter Pitts (1943). A Logical Calculus of the Ideas Immanent in Nervous Activity. Bulletin of Mathematical Biology, Vol. 5, No. 1, pdf
- Donald O. Hebb (1949). The Organization of Behavior. Wiley & Sons
1950 ...
- Stephen C. Kleene (1951) Representation of Events in Nerve Nets and Finite Automata. RM-704, RAND paper, pdf, reprinted in
- Claude Shannon, John McCarthy (eds.) (1956). Automata Studies. Annals of Mathematics Studies, No. 34
- Marvin Minsky (1954). Neural Nets and the Brain Model Problem. Ph.D. dissertation, Princeton University
- B. G. Farley, W. A. Clark (1954). Simulation of Self-Organizing Systems by Digital Computer. IRE Transactions on Information Theory, Vol. 4
- John von Neumann (1956). Probabilistic Logic and the Synthesis of Reliable Organisms From Unreliable Components. in
- Claude Shannon, John McCarthy (eds.) (1956). Automata Studies. Annals of Mathematics Studies, No. 34, pdf
- Nathaniel Rochester, John H. Holland, L. H. Haibt, William L. Duda (1956). Tests on a Cell Assembly Theory of the Action of the Brain, Using a Large Digital Computer. IRE Transactions on Information Theory, Vol. 2, No. 3
- Frank Rosenblatt (1957). The Perceptron - a Perceiving and Recognizing Automaton. Report 85-460-1, Cornell Aeronautical Laboratory [55]
1960 ...
- Bernard Widrow, Marcian Hoff (1960). Adaptive switching circuits. IRE WESCON Convention Record, Vol. 4, pdf
- Henry J. Kelley (1960). Gradient Theory of Optimal Flight Paths. [http://arc.aiaa.org/loi/arsj ARS Journal, Vol. 30, No. 10 » Backpropagation
- Arthur E. Bryson (1961). A gradient method for optimizing multi-stage allocation processes. In Proceedings of the Harvard University Symposium on digital computers and their applications » Backpropagation
- Stuart E. Dreyfus (1961). The numerical solution of variational problems. RAND paper P-2374 » Backpropagation
- Frank Rosenblatt (1962). Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms. Spartan Books
- Alexey G. Ivakhnenko (1965). Cybernetic Predicting Devices. Naukova Dumka
- Marvin Minsky, Seymour Papert (1969). Perceptrons. [56] [57]
1970 ...
- Seppo Linnainmaa (1970). The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors. Master's thesis, University of Helsinki » Backpropagation [58]
- Alexey G. Ivakhnenko (1971). Polynomial theory of complex systems. IEEE Transactions on Systems, Man, and Cybernetics, Vol. 1, No. 4
- A. Harry Klopf (1972). Brain Function and Adaptive Systems - A Heterostatic Theory. Air Force Cambridge Research Laboratories, Special Reports, No. 133, pdf
- Marvin Minsky, Seymour Papert (1972). Perceptrons: An Introduction to Computational Geometry. The MIT Press, 2nd edition with corrections
- Stephen Grossberg (1973). Contour Enhancement, Short Term Memory, and Constancies in Reverberating Neural Networks. Studies in Applied Mathematics, Vol. 52, pdf
- Stephen Grossberg (1974). Classical and instrumental learning by neural networks. Progress in Theoretical Biology. Academic Press
- Paul Werbos (1974). Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph. D. thesis, Harvard University [59] [60]
- Richard Sutton (1978). Single channel theory: A neuronal theory of learning. Brain Theory Newsletter 3, No. 3/4, pp. 72-75. pdf
1980 ...
- Kunihiko Fukushima (1980). Neocognitron: A Self-organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position. Biological Cybernetics, Vol. 36 [61]
- Richard Sutton, Andrew Barto (1981). Toward a modern theory of adaptive networks: Expectation and prediction. Psychological Review, Vol. 88, pp. 135-170. pdf
- Paul Werbos (1982). Applications of advances in nonlinear sensitivity analysis. System Modeling and Optimization, Springer, pdf
- A. Harry Klopf (1982). The Hedonistic Neuron: A Theory of Memory, Learning, and Intelligence. Hemisphere Publishing Corporation, University of Michigan
- David H. Ackley, Geoffrey E. Hinton, Terrence J. Sejnowski (1985). A Learning Algorithm for Boltzmann Machines. Cognitive Science, Vol. 9, No. 1, pdf
- David E. Rumelhart, Geoffrey E. Hinton, Ronald J. Williams (1986). Learning representations by back-propagating errors. Nature, Vol. 323, pdf
1987
- Gerald Tesauro, Terrence J. Sejnowski (1987). A 'Neural' Network that Learns to Play Backgammon. NIPS 1987
- Eric B. Baum, Frank Wilczek (1987). Supervised Learning of Probability Distributions by Neural Networks. NIPS 1987
- A. Harry Klopf (1987). A Neuronal Model of Classical Conditioning. Technical Report, Air Force Wright Aeronautical Laboratories [62]
1988
- Richard Sutton (1988). Learning to Predict by the Methods of Temporal Differences. Machine Learning, Vol. 3, No. 1, pp. 9-44. Kluwer Academic Publishers, Boston. ISSN 0885-6125.
- Gerald Tesauro (1988). Neural network defeats creator in backgammon match. Technical report no. CCSR-88-6, Center for Complex Systems Research, University of Illinois at Urbana-Champaign
- Eric B. Baum, David Haussler (1988). What Size Net Gives Valid Generalization? NIPS 1988
- Eric B. Baum (1988). On the capabilities of multilayer perceptrons. Complexity, Vol. 4, No. 3
- Alan Lapedes, Robert Farber (1988). How Neural Nets Work. pdf
1989
- Andrew Barto, Richard Sutton, Christopher J. C. H. Watkins (1989). Sequential Decision Problems and Neural Networks. NIPS 1989
- Eric B. Baum (1989). The Perceptron Algorithm Is Fast for Non-Malicious Distributions. NIPS 1989
- Eric B. Baum (1989). A Proposal for More Powerful Learning Algorithms. Neural Computation, Vol. 1, No. 2
- Erach A. Irani, John P. Matts, John M. Long, James R. Slagle, POSCH group (1989). Using Artificial Neural Nets for Statistical Discovery: Observations after Using Backpropogation, Expert Systems, and Multiple-Linear Regression on Clinical Trial Data. University of Minnesota, Minneapolis, MN 55455, USA, Complex Systems 3, pdf
- Gerald Tesauro, Terrence J. Sejnowski (1989). A Parallel Network that Learns to Play Backgammon. Artificial Intelligence, Vol. 39, No. 3
- Erol Gelenbe (1989). Random Neural Networks with Negative and Positive Signals and Product Form Solution. Neural Computation, Vol. 1, No. 4
- Xiru Zhang, Michael McKenna, Jill P. Mesirov, David Waltz (1989). An Efficient Implementation of the Back-propagation Algorithm on the Connection Machine CM-2. NIPS 1989
1990 ...
- Paul Werbos (1990). Backpropagation Through Time: What It Does and How to Do It. Proceedings of the IEEE, Vol. 78, No. 10, pdf
- Chris J. Thornton (1990). The Kink Representation for Exclusive-OR. International Neural Network Conference
- Gordon Goetsch (1990). Maximization of Mutual Information in a Context Sensitive Neural Network. Ph.D. thesis
- Vadim Anshelevich (1990). Neural Networks. Review. in Multi Component Systems (Russian)
- Eric B. Baum (1990). Polynomial Time Algorithms for Learning Neural Nets. COLT 1990
- Dennis W. Ruck, Steven K. Rogers, Matthew Kabrisky, Mark E. Oxley, Bruce W. Suter (1990). The multilayer perceptron as an approximation to a Bayes optimal discriminant function. IEEE Transactions on Neural Networks, Vol. 1, No. 4
- Benjamin J. Hellstrom, Laveen N. Kanal (1990). The definition of necessary hidden units in neural networks for combinatorial optimization. IJCNN 1990
- Xiru Zhang, Michael McKenna, Jill P. Mesirov, David Waltz (1990). The backpropagation algorithm on grid and hypercube architectures. Parallel Computing, Vol. 14, No. 3
- Simon Lucas, Robert I. Damper (1990). Syntactic Neural Networks. Connection Science, Vol. 2, No. 3
1991
- Sepp Hochreiter (1991). Untersuchungen zu dynamischen neuronalen Netzen. Diploma thesis, TU Munich, advisor Jürgen Schmidhuber, pdf (German) [63]
- Alex van Tiggelen (1991). Neural Networks as a Guide to Optimization - The Chess Middle Game Explored. ICCA Journal, Vol. 14, No. 3
- Thomas Martinetz, Klaus Schulten (1991). A "Neural-Gas" Network Learns Topologies. In Teuvo Kohonen, Kai Mäkisara, Olli Simula, Jari Kangas (eds.) (1991). Artificial Neural Networks. Elsevier, pdf
- Jürgen Schmidhuber, Rudolf Huber (1991). Using sequential adaptive Neuro-control for efficient Learning of Rotation and Translation Invariance. In Teuvo Kohonen, Kai Mäkisara, Olli Simula, Jari Kangas (eds.) (1991). Artificial Neural Networks. Elsevier
- Jürgen Schmidhuber (1991). Dynamische neuronale Netze und das fundamentale raumzeitliche Lernproblem (Dynamic Neural Nets and the Fundamental Spatio-Temporal Credit Assignment Problem). Ph.D. thesis
- Yoav Freund, David Haussler (1991). Unsupervised Learning of Distributions of Binary Vectors Using 2-Layer Networks. NIPS 1991
- Byoung-Tak Zhang, Gerd Veenker (1991). Neural networks that teach themselves through genetic discovery of novel examples. IEEE IJCNN'91, pdf
- Simon Lucas, Robert I. Damper (1991). Syntactic neural networks in VLSI. VLSI for Artificial Intelligence and Neural Networks
- Simon Lucas (1991). Connectionist architectures for syntactic pattern recognition. Ph.D. thesis, University of Southampton
1992
- Michael Reiss (1992). Temporal Sequence Processing in Neural Networks. Ph.D. thesis, King's College London, advisor John G. Taylor, pdf
- Jacek Mańdziuk, Bohdan Macukow (1992). A Neural Network designed to solve the N-Queens Problem. Biological Cybernetics, Vol. 66 No. 4, pdf
- Gerald Tesauro (1992). Temporal Difference Learning of Backgammon Strategy. ML 1992
- Gerald Tesauro (1992). Practical Issues in Temporal Difference Learning. Machine Learning, Vol. 8, No. 3-4
- Egbert Boers, Herman Kuiper (1992). Biological metaphors and the design of modular artificial neural networks. Master’s thesis, Leiden University, pdf
- Martin Riedmiller, Heinrich Braun (1992). Rprop - A Fast Adaptive Learning Algorithm. Proceedings of the International Symposium on Computer and Information Science
- Justin A. Boyan (1992). Modular Neural Networks for Learning Context-Dependent Game Strategies. Master's thesis, University of Cambridge, pdf
- Patricia Churchland, Terrence J. Sejnowski (1992). The Computational Brain. MIT Press
- Benjamin J. Hellstrom, Laveen N. Kanal (1992). Knapsack packing networks. IEEE Transactions on Neural Networks, Vol. 3, No. 2
- Benjamin J. Hellstrom, Laveen N. Kanal (1992). Asymmetric mean-field neural networks for multiprocessor scheduling. Neural Networks, Vol. 5, No. 4
1993
- Jacek Mańdziuk, Bohdan Macukow (1993). A Neural Network performing Boolean Logic Operations. Optical Memory and Neural Networks, Vol. 2, No. 1, pdf
- Sebastian Thrun, Tom Mitchell (1993). Integrating Inductive Neural Network Learning and Explanation-Based Learning. Proceedings of the 13th IJCAI, Morgan Kaufmann, zipped ps
- Byoung-Tak Zhang, Heinz Mühlenbein (1993). Evolving Optimal Neural Networks Using Genetic Algorithms with Occam's Razor. Complex Systems, Vol. 7, pdf
- Martin Riedmiller, Heinrich Braun (1993). A direct adaptive method for faster backpropagation learning: The RPROP algorithm. IEEE International Conference On Neural Networks, pdf
- Nicol N. Schraudolph, Peter Dayan, Terrence J. Sejnowski (1993). Temporal Difference Learning of Position Evaluation in the Game of Go. NIPS 1993 [64]
1994
- Paul Werbos (1994). The Roots of Backpropagation. From Ordered Derivatives to Neural Networks and Political Forecasting. John Wiley & Sons
- David E. Moriarty, Risto Miikkulainen (1994). Evolving Neural Networks to focus Minimax Search. AAAI-94 » Othello
- Eric Postma (1994). SCAN: A Neural Model of Covert Attention. Ph.D. thesis, Maastricht University, advisor Jaap van den Herik
- Sebastian Thrun (1994). Neural Network Learning in the Domain of Chess. Machines That Learn, Snowbird, Extended abstract
- Christian Posthoff, S. Schawelski, Michael Schlosser (1994). Neural Network Learning in a Chess Endgame Positions. IEEE World Congress on Computational Intelligence
- Alois Heinz (1994). Efficient Neural Net α-β-Evaluators. pdf [65]
- Alois Heinz (1994). Fast bounded smooth regression with lazy neural trees. ICNN 1994, DOI: 10.1109/ICNN.1994.374421
- Martin Riedmiller (1994). Rprop - Description and Implementation Details. Technical Report, University of Karlsruhe, pdf
- Igor Kononenko (1994). On Bayesian Neural Networks. Informatica (Slovenia), Vol. 18, No. 2
1995
- Peter J. Braspenning, Frank Thuijsman, Ton Weijters (eds) (1995). Artificial neural networks: an introduction to ANN theory and practice. LNCS 931, Springer
- David E. Moriarty, Risto Miikkulainen (1995). Discovering Complex Othello Strategies Through Evolutionary Neural Networks. Connection Science, Vol. 7
- Anton Leouski (1995). Learning of Position Evaluation in the Game of Othello. Master's Project, University of Massachusetts, Amherst, Massachusetts, pdf
- Sepp Hochreiter, Jürgen Schmidhuber (1995). Simplifying Neural Nets by Discovering Flat Minima. In Gerald Tesauro, David S. Touretzky and Todd K. Leen (eds.), Advances in Neural Information Processing Systems 7, NIPS'7, pages 529-536. MIT Press
- Sebastian Thrun (1995). Learning to Play the Game of Chess. in Gerald Tesauro, David S. Touretzky, Todd K. Leen (eds.) Advances in Neural Information Processing Systems 7, MIT Press
- Sepp Hochreiter, Jürgen Schmidhuber (1995). Simplifying Neural Nets by Discovering Flat Minima. In Gerald Tesauro, David S. Touretzky and Todd K. Leen (eds.), Advances in Neural Information Processing Systems 7, NIPS'7, pages 529-536. MIT Press
- Sebastian Thrun (1995). Explanation-Based Neural Network Learning - A Lifelong Learning Approach. Ph.D. thesis, University of Bonn, advisors Armin Cremers and Tom Mitchell
- Gerald Tesauro (1995). Temporal Difference Learning and TD-Gammon. Communications of the ACM Vol. 38, No. 3
- Eric Postma (1995). Optimization Networks. Artificial Neural Networks
- Jacek Jelonek, Krzysztof Krawiec, Roman Slowinski (1995). Rough Set Reduction of Attributes and their Domains for Neural Networks. Computational Intelligence, Vol. 11, No. 2
- Omar Syed (1995). Applying Genetic Algorithms to Recurrent Neural Networks for Learning Network Parameters and Architecture, Masters Thesis, Case Western Reserve University
- Pascal Tang (1995). Forecasting with Neural networks. ICANN 1995
- Marco Wiering (1995). TD Learning of Game Evaluation Functions with Hierarchical Neural Architectures. Master's thesis, University of Amsterdam, pdf
- Michael A Arbib (ed.) (1995, 2002). The Handbook of Brain Theory and Neural Networks. The MIT Press
- Nicol N. Schraudolph (1995). Optimization of Entropy with Neural Networks. Ph.D. thesis, University of California, San Diego
- Alois Heinz (1995). Pipelined Neural Tree Learning by Error Forward-Propagation. ICNN 1995, DOI: 10.1109/ICNN.1995.488132, pdf
- Alois Heinz, Christoph Hense (1995). Tools for Neural Trees. Technical Report No. 68
- Nicol N. Schraudolph, Terrence J. Sejnowski (1995). Tempering Backpropagation Networks: Not All Weights are Created Equal. NIPS 1995, pdf
1996
- Sebastian Thrun (1996). Explanation-Based Neural Network Learning: A Lifelong Learning Approach. Kluwer Academic Publishers
- Wee Sun Lee (1996). Agnostic Learning and Single Hidden Layer Neural Networks. Ph.D. thesis, Australian National University, ps
- Markus Enzenberger (1996). The Integration of A Priori Knowledge into a Go Playing Neural Network.
- Pieter Spronck (1996). Elegance: Genetic Algorithms in Neural Reinforcement Control. Master thesis, Delft University of Technology, pdf
- Raúl Rojas (1996). Neural Networks - A Systematic Introduction. Springer, available as pdf ebook
- Ida Sprinkhuizen-Kuyper, Egbert J. W. Boers (1996). The Error Surface of the Simplest XOR Network Has Only Global Minima. Neural Computation, Vol. 8, No. 6, pdf
1997
- Sepp Hochreiter, Jürgen Schmidhuber (1997). Long short-term memory. Neural Computation, Vol. 9, No. 8, pdf [66]
- Kieran Greer, Piyush Ojha, David A. Bell (1997). Learning Search Heuristics from Examples: A Study in Computer Chess. Seventh Conference of the Spanish Association for Artificial Intelligence, CAEPIA’97, November, pp. 695-704.
- Don Beal, Martin C. Smith (1997). Learning Piece Values Using Temporal Differences. ICCA Journal, Vol. 20, No. 3
- Frank M. Thiesing, Oliver Vornberger (1997). Forecasting Sales Using Neural Networks. Fuzzy Days 1997, pdf
- Simon Lucas (1997). Forward-Backward Building Blocks for Evolving Neural Networks with Intrinsic Learning Behaviors. IWANN 1997
1998
- Kieran Greer (1998). A Neural Network Based Search Heuristic and its Application to Computer Chess. D.Phil. Thesis, University of Ulster
- Nobusuke Sasaki, Yasuji Sawada, Jin Yoshimura (1998). A Neural Network Program of Tsume-Go. CG 1998 [67]
- Krzysztof Krawiec, Roman Slowinski, Irmina Szczesniak (1998). Pedagogical Method for Extraction of Symbolic Knowledge from Neural Networks. Rough Sets and Current Trends in Computing 1998
- Steven Walczak (1998). Neural network models for a resource allocation problem. IEEE Transactions on Systems, Man, and Cybernetics, Part B 28(2)
- Jonathan Baxter, Andrew Tridgell, Lex Weaver (1998). Experiments in Parameter Learning Using Temporal Differences. ICCA Journal, Volume 21 No. 2, pdf
- Guy Haworth, Meel Velliste (1998). Chess Endgames and Neural Networks. ICCA Journal, Vol. 21, No. 4
- Don Beal, Martin C. Smith (1998). First Results from Using Temporal Difference Learning in Shogi. CG 1998
- Nicol N. Schraudolph (1998). Centering Neural Network Gradient Factors. Neural Networks: Tricks of the Trade
- Toshinori Munakata (1998). Fundamentals of the New Artificial Intelligence: Beyond Traditional Paradigms. 1st edition, Springer, 2nd edition 2008
- Lex Weaver, Terry Bossomaier (1998). Evolution of Neural Networks to Play the Game of Dots-and-Boxes. arXiv:cs/9809111
- Norman Richards, David E. Moriarty, Risto Miikkulainen (1998). Evolving Neural Networks to Play Go. Applied Intelligence, Vol. 8, No. 1
1999
- Kumar Chellapilla, David B. Fogel (1999). Evolution, Neural Networks, Games, and Intelligence. Proceedings of the IEEE, September, pp. 1471-1496. CiteSeerX
- Kumar Chellapilla, David B. Fogel (1999). Evolving Neural Networks to Play Checkers without Expert Knowledge. IEEE Transactions on Neural Networks, Vol. 10, No. 6, pp. 1382-1391.
- Kieran Greer, Piyush Ojha, David A. Bell (1999). A Pattern-Oriented Approach to Move Ordering: the Chessmaps Heuristic. ICCA Journal, Vol. 22, No. 1
- Anna Górecka, Maciej Szmit (1999). Exchange rates prediction by ARIMA and Neural Networks Models. 47th International Atlantic Economic Conerence (Abstract: International Advances of Economic Research Vol 5 Nr 4 Nov. 1999, St Louis, MO, USA 1999), pdf
- Don Beal, Martin C. Smith (1999). Learning Piece-Square Values using Temporal Differences. ICCA Journal, Vol. 22, No. 4
- Simon S. Haykin (1999). Neural Networks: A Comprehensive Foundation. 2nd Edition, Prentice-Hall
- Laurence F. Abbott, Terrence J. Sejnowski (eds.) (1999). Neural Codes and Distributed Representations. MIT Press
- Geoffrey E. Hinton, Terrence J. Sejnowski (eds.) (1999). Unsupervised Learning: Foundations of Neural Computation. MIT Press
- Peter Dayan (1999). Recurrent Sampling Models for the Helmholtz Machine. Neural Computation, Vol. 11, No. 3, pdf [68]
- Ida Sprinkhuizen-Kuyper, Egbert J. W. Boers (1999). A local minimum for the 2-3-1 XOR network. IEEE Transactions on Neural Networks, Vol. 10, No. 4
2000 ...
- Levente Kocsis, Jos Uiterwijk, Jaap van den Herik (2000). Learning Time Allocation using Neural Networks. CG 2000
- Peter Auer, Stephen Kwek, Wolfgang Maass, Manfred K. Warmuth (2000). Learning of Depth Two Neural Networks with Constant Fan-in at the Hidden Nodes. Electronic Colloquium on Computational Complexity, Vol. 7
- Jonathan Baxter, Andrew Tridgell, Lex Weaver (2000). Learning to Play Chess Using Temporal Differences. Machine Learning, Vol 40, No. 3, pdf
- Alois Heinz (2000). Tree-Structured Neural Networks: Efficient Evaluation of Higher-Order Derivatives and Integrals. IJCNN 2000
- Robert Levinson, Ryan Weber (2000). Chess Neighborhoods, Function Combination, and Reinforcement Learning. CG 2000, pdf
- Matthias Lüscher (2000). Automatic Generation of an Evaluation Function for Chess Endgames. ETH Zurich Supervisors: Thomas Lincke and Christoph Wirth, pdf » Endgame
- Miroslav Kubat (2000). Designing neural network architectures for pattern recognition. The Knowledge Engineering Review, Vol. 15, No. 2
- Igor Aizenberg, Naum N. Aizenberg, Joos Vandewalle (2000). Multi-Valued and Universal Binary Neurons: Theory, Learning and Applications. Springer [69]
2001
- Erik van der Werf, Jaap van den Herik (2001). Visual Learning in Go. 6th Computer Olympiad Workshop, pdf
- Levente Kocsis, Jos Uiterwijk, Jaap van den Herik (2001). Move Ordering using Neural Networks. IEA/AIE 2001, LNCS 2070, pdf
- Kee Siong Ng (2001). Neural Networks for Structured Data. BSc-Thesis, zipped ps
- Peter Dayan, Laurence F. Abbott (2001, 2005). Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. MIT Press
2002
- Levente Kocsis, Jos Uiterwijk, Eric Postma, Jaap van den Herik (2002). The Neural MoveMap Heuristic in Chess. CG 2002
- Erik van der Werf, Jos Uiterwijk, Eric Postma, Jaap van den Herik (2002). Local Move Prediction in Go. CG 2002
- Gerald Tesauro (2002). Programming backgammon using self-teaching neural nets. Artificial Intelligence Vol. 134 No. 1-2
- Mark Winands, Levente Kocsis, Jos Uiterwijk, Jaap van den Herik (2002). Temporal difference learning and the Neural MoveMap heuristic in the game of Lines of Action. in GAME-ON 2002, pdf
- Jacek Mańdziuk (2002). Neural Networks for the N-Queens Problem: a Review. Control and Cybernetics, Vol. 31, No. 2, pdf
- Moshe Sipper (2002) Machine Nature: The Coming Age of Bio-Inspired Computing. McGraw-Hill, New York
- Paul E. Utgoff, David J. Stracuzzi (2002). Many-Layered Learning. Neural Computation, Vol. 14, No. 10, pdf
- Michael I. Jordan, Terrence J. Sejnowski (eds.) (2002). Graphical Models: Foundations of Neural Computation. MIT Press
- Kenneth O. Stanley, Risto Miikkulainen (2002). Evolving Neural Networks Through Augmenting Topologies. Evolutionary Computation, Vol. 10, No. 2
2003
- Levente Kocsis (2003). Learning Search Decisions. Ph.D thesis, Maastricht University, pdf
- Markus Enzenberger (2003). Evaluation in Go by a Neural Network using Soft Segmentation. Advances in Computer Games 10, pdf
- Alois Heinz (2003). Yes, Trees May Have Neurons. Computer Science in Perspective 2003
2004
- Jan Peter Patist, Marco Wiering (2004). Learning to Play Draughts using Temporal Difference Learning with Neural Networks and Databases. Cognitive Artificial Intelligence, Utrecht University, Benelearn’04
- Henk Mannen, Marco Wiering (2004). Learning to play chess using TD(λ)-learning with database games. Cognitive Artificial Intelligence, Utrecht University, Benelearn’04, pdf
- Mathieu Autonès, Aryel Beck, Phillippe Camacho, Nicolas Lassabe, Hervé Luga, François Scharffe (2004). Evaluation of Chess Position by Modular Neural network Generated by Genetic Algorithm. EuroGP 2004 [70]
- Daniel Walker, Robert Levinson (2004). The MORPH Project in 2004. ICGA Journal, Vol. 27, No. 4
2006
- Holk Cruse (2006). Neural Networks as Cybernetic Systems. 2nd and revised edition, Department of Biological Cybernetics, Bielefeld University
- Geoffrey E. Hinton, Simon Osindero, Yee Whye Teh (2006). A Fast Learning Algorithm for Deep Belief Nets. Neural Computation, Vol. 18, No. 7, pdf
- Geoffrey E. Hinton, Ruslan R. Salakhutdinov (2006). Reducing the Dimensionality of Data with Neural Networks. Science, Vol. 313, pdf
2007
- Edward P. Manning (2007). Temporal Difference Learning of an Othello Evaluation Function for a Small Neural Network with Shared Weights. IEEE Symposium on Computational Intelligence and AI in Games
- Yong Duan, Baoxia Cui, Xinhe Xu (2007). State Space Partition for Reinforcement Learning Based on Fuzzy Min-Max Neural Network. ISNN 2007
- David Kriesel (2007). A Brief Introduction to Neural Networks. available at [1]
- Roland Stuckardt (2007). Applying Backpropagation Networks to Anaphor Resolution. In: António Branco (Ed.), Anaphora: Analysis, Algorithms, and Applications. Selected Papers of the 6th Discourse Anaphora and Anaphor Resolution Colloquium, DAARC 2007, Lagos, Portugal
2008
- Ilya Sutskever, Vinod Nair (2008). Mimicking Go Experts with Convolutional Neural Networks. ICANN 2008, pdf
- Simon S. Haykin (2008). Neural Networks: A Comprehensive Foundation. 3rd Edition, [2]
- Toshinori Munakata (2008). Fundamentals of the New Artificial Intelligence: Neural, Evolutionary, Fuzzy and More. 2nd edition, Springer, 1st edition 1998
- Byoung-Tak Zhang (2008). Hypernetworks: A molecular evolutionary architecture for cognitive learning and memory. IEEE Computational Intelligence Magazine, Vol. 3, No. 3, pdf
- Qing Song, James C. Spall, Yeng Chai Soh, Jie Ni (2008). Robust Neural Network Tracking Controller Using Simultaneous Perturbation Stochastic Approximation. IEEE Transactions on Neural Networks, Vol. 19, No. 5, 2003 pdf » SPSA
2009
- Daniel Abdi, Simon Levine, Girma T. Bitsuamlak (2009). Application of an Artificial Neural Network Model for Boundary Layer Wind Tunnel Profile Development. 11th Americas conference on wind Engineering, pdf
2010 ...
- Ian Stewart, Wenying Feng, Selim Akl (2010). Tuning Neural Networks by Both Connectivity and Size. ITNG 2010
2011
- Jonathan K. Vis (2011). Discrete Tomography: A Neural Network Approach. Master's thesis, Leiden University, pdf
- Jonathan K. Vis, Walter Kosters, Joost Batenburg (2011). Discrete Tomography: A Neural Network Approach. BNAIC 2011 pdf
- Nikolaos Papahristou, Ioannis Refanidis (2011). Training Neural Networks to Play Backgammon Variants Using Reinforcement Learning. Proceedings of Evogames 2011, Part I, LNCS 6624, pdf
2012
- Sjoerd van den Dries, Marco Wiering (2012). Neural-fitted TD-leaf learning for playing Othello with structured neural networks. IEEE Transactions on Neural Networks and Learning Systems, Vol. 23, No. 11
- Jürgen Schmidhuber, Faustino Gomez, Santiago Fernández, Alex Graves, Sepp Hochreiter (2012). Sequence Learning with Artificial Recurrent Neural Networks. (Aiming to become the definitive textbook on RNN.) Invited by Cambridge University Press
- Peter McLeod, Brijesh Verma (2012). Clustered ensemble neural network for breast mass classification in digital mammography. IJCNN 2012
- Grégoire Montavon, Geneviève B. Orr, Klaus-Robert Müller (eds.) (2012). Neural Networks: Tricks of the Trade. (2nd Edition) LNCS 7700, Springer
- Nicol N. Schraudolph (2012). Centering Neural Network Gradient Factors.
- Léon Bottou (2012). Stochastic Gradient Descent Tricks. Microsoft Research, pdf
- Ronan Collobert, Koray Kavukcuoglu, Clément Farabet (2012). Implementing Neural Networks Efficiently. [71]
2013
- Grégoire Montavon (2013). On Layer-Wise Representations in Deep Neural Networks. Ph.D. Thesis, TU Berlin, advisor Klaus-Robert Müller
- Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, Martin Riedmiller (2013). Playing Atari with Deep Reinforcement Learning. arXiv:1312.5602 [72]
- Risto Miikkulainen (2013). Evolving Neural Networks. IJCNN 2013, pdf
2014
- Yann Dauphin, Razvan Pascanu, Caglar Gulcehre, Kyunghyun Cho, Surya Ganguli, Yoshua Bengio (2014). Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. arXiv:1406.2572 [73]
- Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio (2014). Generative Adversarial Networks. arXiv:1406.2661v1 [74]
- Christopher Clark, Amos Storkey (2014). Teaching Deep Convolutional Neural Networks to Play Go. arXiv:1412.3409 [75] [76]
- Chris J. Maddison, Aja Huang, Ilya Sutskever, David Silver (2014). Move Evaluation in Go Using Deep Convolutional Neural Networks. arXiv:1412.6564v1 » Go
- Ilya Sutskever, Oriol Vinyals, Quoc V. Le (2014). Sequence to Sequence Learning with Neural Networks. arXiv:1409.3215
2015
- Diederik P. Kingma, Jimmy Lei Ba (2015). Adam: A Method for Stochastic Optimization. arXiv:1412.6980v8, ICLR 2015 [77]
- Michael Nielsen (2015). Neural networks and deep learning. Determination Press
- Sergey Ioffe, Christian Szegedy (2015). Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv:1502.03167
- Geoffrey E. Hinton, Oriol Vinyals, Jeff Dean (2015). Distilling the Knowledge in a Neural Network. arXiv:1503.02531
- James L. McClelland (2015). Explorations in Parallel Distributed Processing: A Handbook of Models, Programs, and Exercises. Second Edition, Contents
- Gábor Melis (2015). Dissecting the Winning Solution of the HiggsML Challenge. NIPS 2014
- Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A. Rusu, Joel Veness, Marc G. Bellemare, Alex Graves, Martin Riedmiller, Andreas K. Fidjeland, Georg Ostrovski, Stig Petersen, Charles Beattie, Amir Sadik, Ioannis Antonoglou, Helen King, Dharshan Kumaran, Daan Wierstra, Shane Legg, Demis Hassabis (2015). Human-level control through deep reinforcement learning. Nature, Vol. 518
- Jürgen Schmidhuber (2015). Deep Learning in Neural Networks: An Overview. Neural Networks, Vol. 61
- Zachary C. Lipton, John Berkowitz, Charles Elkan (2015). A Critical Review of Recurrent Neural Networks for Sequence Learning. arXiv:1506.00019v4
- Douglas Bagnall (2015). Author Identification using Multi-headed Recurrent Neural Networks. arXiv:1506.04891
- Guillaume Desjardins, Karen Simonyan, Razvan Pascanu, Koray Kavukcuoglu (2015). Natural Neural Networks. arXiv:1507.00210
- Barak Oshri, Nishith Khandwala (2015). Predicting Moves in Chess using Convolutional Neural Networks. pdf [78] [79]
- Yann LeCun, Yoshua Bengio, Geoffrey E. Hinton (2015). Deep Learning. Nature, Vol. 521 [80]
- Matthew Lai (2015). Giraffe: Using Deep Reinforcement Learning to Play Chess. M.Sc. thesis, Imperial College London, arXiv:1509.01549v1 » Giraffe
- Nikolai Yakovenko, Liangliang Cao, Colin Raffel, James Fan (2015). Poker-CNN: A Pattern Learning Strategy for Making Draws and Bets in Poker Games. arXiv:1509.06731
- Emmanuel Bengio, Pierre-Luc Bacon, Joelle Pineau, Doina Precup (2015). Conditional Computation in Neural Networks for faster models. arXiv:1511.06297
- Ilya Loshchilov, Frank Hutter (2015). Online Batch Selection for Faster Training of Neural Networks. arXiv:1511.06343
- Yuandong Tian, Yan Zhu (2015). Better Computer Go Player with Neural Network and Long-term Prediction. arXiv:1511.06410 [81] [82] » Go
- Peter H. Jin, Kurt Keutzer (2015). Convolutional Monte Carlo Rollouts in Go. arXiv:1512.03375
- Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun (2015). Deep Residual Learning for Image Recognition. arXiv:1512.03385
- Nicolas Heess, Jonathan J. Hunt, Timothy Lillicrap, David Silver (2015). Memory-based control with recurrent neural networks. arXiv:1512.04455
2016
- Dharshan Kumaran, Demis Hassabis, James L. McClelland (2016). What learning systems do intelligent agents need? Complementary Learning Systems Theory Updated. Trends in Cognitive Sciences, Vol. 20, No. 7, pdf
- Ziyu Wang, Nando de Freitas, Marc Lanctot (2016). Dueling Network Architectures for Deep Reinforcement Learning. arXiv:1511.06581
- David Silver, Aja Huang, Chris J. Maddison, Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, Sander Dieleman, Dominik Grewe, John Nham, Nal Kalchbrenner, Ilya Sutskever, Timothy Lillicrap, Madeleine Leach, Koray Kavukcuoglu, Thore Graepel, Demis Hassabis (2016). Mastering the game of Go with deep neural networks and tree search. Nature, Vol. 529 » AlphaGo
- Tobias Graf, Marco Platzner (2016). Using Deep Convolutional Neural Networks in Monte Carlo Tree Search. CG 2016
- Aja Huang (2016). AlphaGo: Combining Deep Neural Networks with Tree Search. CG 2016, Keynote Lecture
- Peter H. Jin , Kurt Keutzer (2016). Convolutional Monte Carlo Rollouts for Computer Go. CG 2016
- Hung Guei, Tinghan Wei, Jin-Bo Huang, I-Chen Wu (2016). An Empirical Study on Applying Deep Reinforcement Learning to the Game 2048. CG 2016
- Omid E. David, Nathan S. Netanyahu, Lior Wolf (2016). DeepChess: End-to-End Deep Neural Network for Automatic Learning in Chess. ICAAN 2016, Lecture Notes in Computer Science, Vol. 9887, Springer, pdf preprint » DeepChess [83] [84]
- Dror Sholomon, Omid E. David, Nathan S. Netanyahu (2016). DNN-Buddies: A Deep Neural Network-Based Estimation Metric for the Jigsaw Puzzle Problem. ICAAN 2016, Lecture Notes in Computer Science, Vol. 9887, Springer [85]
- Ian Goodfellow, Yoshua Bengio, Aaron Courville (2016). Deep Learning. MIT Press
- Volodymyr Mnih, Adrià Puigdomènech Badia, Mehdi Mirza, Alex Graves, Timothy Lillicrap, Tim Harley, David Silver, Koray Kavukcuoglu (2016). Asynchronous Methods for Deep Reinforcement Learning. arXiv:1602.01783v2
- Vincent Dumoulin, Francesco Visin (2016). A guide to convolution arithmetic for deep learning. arXiv:1603.07285
- Patricia Churchland, Terrence J. Sejnowski (2016). The Computational Brain, 25th Anniversary Edition. MIT Press
- Ilya Loshchilov, Frank Hutter (2016). CMA-ES for Hyperparameter Optimization of Deep Neural Networks. arXiv:1604.07269 [86]
- Audrūnas Gruslys, Rémi Munos, Ivo Danihelka, Marc Lanctot, Alex Graves (2016). Memory-Efficient Backpropagation Through Time. arXiv:1606.03401
- Andrei A. Rusu, Neil C. Rabinowitz, Guillaume Desjardins, Hubert Soyer, James Kirkpatrick, Koray Kavukcuoglu, Razvan Pascanu, Raia Hadsell (2016). Progressive Neural Networks. arXiv:1606.04671
- Douglas Bagnall (2016). Authorship clustering using multi-headed recurrent neural networks. arXiv:1608.04485
- Gao Huang, Zhuang Liu, Laurens van der Maaten, Kilian Q. Weinberger (2016). Densely Connected Convolutional Networks. arXiv:1608.06993 [87]
- George Rajna (2016). Deep Neural Networks. viXra:1609.0126
- James Kirkpatrick, Razvan Pascanu, Neil C. Rabinowitz, Joel Veness, Guillaume Desjardins, Andrei A. Rusu, Kieran Milan, John Quan, Tiago Ramalho, Agnieszka Grabska-Barwinska, Demis Hassabis, Claudia Clopath, Dharshan Kumaran, Raia Hadsell (2016). Overcoming catastrophic forgetting in neural networks. arXiv:1612.00796 [88]
- Zhenxing Niu, Mo Zhou, Le Wang, Xinbo Gao, Gang Hua (2016). Ordinal Regression with Multiple Output CNN for Age Estimation. CVPR 2016, pdf
- Li Jing, Yichen Shen, Tena Dubček, John Peurifoy, Scott Skirlo, Yann LeCun, Max Tegmark, Marin Soljačić (2016). Tunable Efficient Unitary Neural Networks (EUNN) and their application to RNNs. arXiv:1612.05231
2017
- Yutian Chen, Matthew W. Hoffman, Sergio Gomez Colmenarejo, Misha Denil, Timothy Lillicrap, Matthew Botvinick, Nando de Freitas (2017). Learning to Learn without Gradient Descent by Gradient Descent. arXiv:1611.03824v6, ICML 2017
- Brian Chu, Daylen Yang, Ravi Tadinada (2017). Visualizing Residual Networks. arXiv:1701.02362
- Muthuraman Chidambaram, Yanjun Qi (2017). Style Transfer Generative Adversarial Networks: Learning to Play Chess Differently. arXiv:1702.06762v1 [89]
- George Rajna (2017). Artificial Neural Network. viXra:1702.0130
- Raúl Rojas (2017). Deepest Neural Networks. arXiv:1707.02617
- Matej Moravčík, Martin Schmid, Neil Burch, Viliam Lisý, Dustin Morrill, Nolan Bard, Trevor Davis, Kevin Waugh, Michael Johanson, Michael Bowling (2017). DeepStack: Expert-level artificial intelligence in heads-up no-limit poker. Science, Vol. 356, No. 6337
- Xinqi Zhu, Michael Bain (2017). B-CNN: Branch Convolutional Neural Network for Hierarchical Classification. arXiv:1709.09890, GitHub - zhuxinqimac/B-CNN: Sample code of B-CNN paper
- Matthia Sabatelli (2017). Learning to Play Chess with Minimal Lookahead and Deep Value Neural Networks. Master's thesis, University of Groningen, pdf [90]
- David Silver, Julian Schrittwieser, Karen Simonyan, Ioannis Antonoglou, Aja Huang, Arthur Guez, Thomas Hubert, Lucas Baker, Matthew Lai, Adrian Bolton, Yutian Chen, Timothy Lillicrap, Fan Hui, Laurent Sifre, George van den Driessche, Thore Graepel, Demis Hassabis (2017). Mastering the game of Go without human knowledge. Nature, Vol. 550 [91]
- David Silver, Thomas Hubert, Julian Schrittwieser, Ioannis Antonoglou, Matthew Lai, Arthur Guez, Marc Lanctot, Laurent Sifre, Dharshan Kumaran, Thore Graepel, Timothy Lillicrap, Karen Simonyan, Demis Hassabis (2017). Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. arXiv:1712.01815 » AlphaZero [92]
- Tristan Cazenave (2017). Residual Networks for Computer Go. IEEE Transactions on Computational Intelligence and AI in Games, Vol. PP, No. 99, pdf [93]
- Kei Takada, Hiroyuki Iizuka, Masahito Yamamoto (2017). Reinforcement Learning for Creating Evaluation Function Using Convolutional Neural Network in Hex. TAAI 2017 » Hex
- Chao Gao, Martin Müller, Ryan Hayward (2017). Focused Depth-first Proof Number Search using Convolutional Neural Networks for the Game of Hex. IJCAI 2017
- Thomas Elsken, Jan Hendrik Metzen, Frank Hutter (2017). Simple And Efficient Architecture Search for Convolutional Neural Networks. arXiv:1711.04528
- Joel Veness, Tor Lattimore, Avishkar Bhoopchand, Agnieszka Grabska-Barwinska, Christopher Mattern, Peter Toth (2017). Online Learning with Gated Linear Networks. arXiv:1712.01897
- Qiming Chen, Ren Wu (2017). CNN Is All You Need. arXiv:1712.09662
- Alexantrou Serb, Edoardo Manino, Ioannis Messaris, Long Tran-Thanh, Themis Prodromakis (2017). Hardware-level Bayesian inference. NIPS 2017 » Analog Evaluation
2018
- Yu Nasu (2018). ƎUИИ Efficiently Updatable Neural-Network based Evaluation Functions for Computer Shogi. Ziosoft Computer Shogi Club, pdf, pdf (Japanese with English abstract) GitHub - asdfjkl/nnue translation » NNUE [94]
- Kei Takada, Hiroyuki Iizuka, Masahito Yamamoto (2018). Computer Hex Algorithm Using a Move Evaluation Method Based on a Convolutional Neural Network. Communications in Computer and Information Science » Hex
- Matthia Sabatelli, Francesco Bidoia, Valeriu Codreanu, Marco Wiering (2018). Learning to Evaluate Chess Positions with Deep Neural Networks and Limited Lookahead. ICPRAM 2018, pdf
- Ashwin Srinivasan, Lovekesh Vig, Michael Bain (2018). Logical Explanations for Deep Relational Machines Using Relevance Information. arXiv:1807.00595
- Thomas Elsken, Jan Hendrik Metzen, Frank Hutter (2018). Neural Architecture Search: A Survey. arXiv:1808.05377
- David Silver, Thomas Hubert, Julian Schrittwieser, Ioannis Antonoglou, Matthew Lai, Arthur Guez, Marc Lanctot, Laurent Sifre, Dharshan Kumaran, Thore Graepel, Timothy Lillicrap, Karen Simonyan, Demis Hassabis (2018). A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science, Vol. 362, No. 6419 [95]
- Chao Gao, Siqi Yan, Ryan Hayward, Martin Müller (2018). A transferable neural network for Hex. ICGA Journal, Vol. 40, No. 3
2019
- Marius Lindauer, Frank Hutter (2019). Best Practices for Scientific Research on Neural Architecture Search. arXiv:1909.02453
- Guy Haworth (2019). Chess endgame news: an endgame challenge for neural nets. ICGA Journal, Vol. 41, No. 3 » Endgame
- Philip G. Breen, Christopher N. Foley, Tjarda Boekholt, Simon Portegies Zwart (2019). Newton vs the machine: solving the chaotic three-body problem using deep neural networks. arXiv:1910.07291
2020 ...
- Reid McIlroy-Young, Siddhartha Sen, Jon Kleinberg, Ashton Anderson (2020). Aligning Superhuman AI with Human Behavior: Chess as a Model System. ACM SIGKDD 2020, arXiv:2006.01855 » Maia Chess
- Reid McIlroy-Young, Russell Wang, Siddhartha Sen, Jon Kleinberg, Ashton Anderson (2020). Learning Personalized Models of Human Behavior in Chess. arXiv:2008.10086
- Oisín Carroll, Joeran Beel (2020). Finite Group Equivariant Neural Networks for Games. arXiv:2009.05027
- Mohammad Pezeshki, Sékou-Oumar Kaba, Yoshua Bengio , Aaron Courville , Doina Precup, Guillaume Lajoie (2020). Gradient Starvation: A Learning Proclivity in Neural Networks. arXiv:2011.09468
- Johannes Czech, Moritz Willig, Alena Beyer, Kristian Kersting, Johannes Fürnkranz (2020). Learning to Play the Chess Variant Crazyhouse Above World Champion Level With Deep Neural Networks and Human Data. Frontiers in Artificial Intelligence » CrazyAra
2021
- Dominik Klein (2021). Neural Networks For Chess. Release Version 1.1 · GitHub [96]
- Thomas McGrath, Andrei Kapishnikov, Nenad Tomašev, Adam Pearce, Demis Hassabis, Been Kim, Ulrich Paquet, Vladimir Kramnik (2021). Acquisition of Chess Knowledge in AlphaZero. arXiv:2111.09259 [97]
Blog & Forum Posts
1996 ...
- Q: Neural Nets/Genetic Algor. and Chess by Jeff Hamm, rgcc, March 01, 1996
- neural networks for pawn-structures by Romain Slootmaekers, rgcc, March 29, 1996
- Neural Network based Chessprogram by Michael Niemeck, rgcc, April 16, 1996
- Neural Nets in Chess? Question to experts by George R. Barrett, rgcc, February 02, 1997
- Chess using Neural Networks/Fuzzy Logic by Kumar Chellapilla, rgcc, February 12, 1997
- Evaluation by neural network ? by Mark Taylor, CCC, November 10, 1997
- Re: Evaluation by neural network ? by Jay Scott, CCC, November 10, 1997 [98]
- neural network and chess by Yeeming Jih, rgcc, April 23, 1998
- Chess, Backgammon and Neural Nets (NN) by Torsten Schoop, CCC, August 20, 1998
- Chess and Neural Networks by Frank Schubert, CCC, January 27, 1999
- Neural networks by Bill Keller, rgcc, September 01, 1999
- neural computing in eval function by Tijs van Dam, CCC, December 20, 1999
2000 ...
- Whatever happened to Neural Network Chess programs? by Ray Lopez, rgcc, March 26, 2000
- Re: Whatever happened to Neural Network Chess programs? by Andy Walker, rgcc, March 28, 2000 » Advances in Computer Chess 1, Ron Atkin
- Combining Neural Networks and Alpha-Beta by Matthias Lüscher, rgcc, April 01, 2000 » Chessterfield
- Neural Networks in Chess by Guy Haworth, CCC, June 23, 2000
- Artificial Neural Networks for Chess by Jet Nebula, rgcc, April 02, 2002
- chess and neural networks by Ralph Stoesser, CCC, July 01, 2003
- Presentation for a neural net learning chess program by Dann Corbit, CCC, April 06, 2004 [99]
- Neural nets in backgammon by Albert Silver, CCC, April 07, 2004
- Chess Neural Network: ANOTHER VICTORY FOR OCTAVIUS! by Luke Pellen, rgcc, May 04, 2004
2005 ...
- designing neural networks by Gerd Isenberg, CCC, August 31, 2007
- naive bayes classifier by Don Dailey, CCC, July 21, 2009 [100]
2010 ...
- Chess program with Artificial Neural Networks (ANN)? by Stephan Vermeire, CCC, January 07, 2010
- Re: Chess program with Artificial Neural Networks (ANN)? by Gian-Carlo Pascutto, CCC, January 07, 2010 » Stoofvlees
- Re: Chess program with Artificial Neural Networks (ANN)? by Gian-Carlo Pascutto, CCC, January 08, 2010
- Re: Chess program with Artificial Neural Networks (ANN)? by Volker Annuss, CCC, January 08, 2010 » Hermann
- Is there place for neural networks in chess engines? by E Diaz, CCC, December 02, 2011
- What does the hidden layer in a neural network compute? by GeorgeMcDowd, Cross Validated, July 02, 2013
- Move Evaluation in Go Using Deep Convolutional Neural Networks by Aja Huang, The Computer-go Archives, December 19, 2014
2015 ...
- If you are interested in machine learning and Python ! by Ruxy Sylwyka, CCC, February 23, 2015
- *First release* Giraffe, a new engine based on deep learning by Matthew Lai, CCC, July 08, 2015 » Giraffe
2016
- Neural networks for Spanish checkers and beyond by Alvaro, Game-AI Forum, January 01, 2016
- Chess position evaluation with convolutional neural network in Julia by Kamil Czarnogorski, Machine learning with Julia and python, April 02, 2016 [101]
- Deep Learning Chess Engine ? by Eren Yavuz, CCC, July 21, 2016
- Re: Deep Learning Chess Engine ? by Alexandru Mosoi, CCC, July 21, 2016 » Zurichess
- Re: Deep Learning Chess Engine ? by Matthew Lai, CCC, August 04, 2016 » Giraffe [102]
- Neuronet plus conventional approach combined? by Rasmus Althoff, CCC, September 02, 2016
- DeepChess: Another deep-learning based chess program by Matthew Lai, CCC, October 17, 2016 » DeepChess
- The scaling of Deep Learning MCTS Go engines by Kai Laskos, CCC, October 23, 2016 » Deep Learning, Go, MCTS
2017
- Deep Pink: a chess engine using deep learning by Chao Ma, CCC, February 05, 2017 » Deep Pink
- Using GAN to play chess by Evgeniy Zheltonozhskiy, CCC, February 23, 2017 [103]
- Is AlphaGo approach unsuitable to chess? by Mel Cooper, CCC, May 27, 2017 » AlphaGo, Deep Learning, Giraffe
- Re: Is AlphaGo approach unsuitable to chess? by Peter Österlund, CCC, May 31, 2017 » Texel
- Neural nets for Go - chain pooling? by David Wu, Computer Go Archive, August 18, 2017
- AlphaGo Zero: Learning from scratch by Demis Hassabis and David Silver, DeepMind, October 18, 2017
- We are doomed - AlphaGo Zero, learning only from basic rules by Vincent Lejeune, CCC, October 18, 2017
- AlphaGo Zero by Alberto Sanjuan, CCC, October 19, 2017
- Zero performance by Gian-Carlo Pascutto, Computer Go Archive, October 20, 2017
- Re: AlphaGo Zero by Hendrik Baier, Computer Go Archive, October 20, 2017
- Neural networks for chess position evaluation- request by Kamil Czarnogorski, CCC, November 13, 2017 » Evaluation
- AlphaGo's evaluation function by Jens Kipper, CCC, November 26, 2017
- Neural Nets can't explain what they do and this is a problem by Myron Samsin, November 26, 2017
- Google's AlphaGo team has been working on chess by Peter Kappler, CCC, December 06, 2017 » AlphaZero
- Historic Milestone: AlphaZero by Miguel Castanuela, CCC, December 06, 2017
- An AlphaZero inspired project by Truls Edvard Stokke, CCC, December 14, 2017 » AlphaZero
2018
- Announcing lczero by Gary, CCC, January 09, 2018 » Leela Chess Zero
- Connect 4 AlphaZero implemented using Python... by Steve Maughan, CCC, January 29, 2018 » AlphaZero, Connect Four, Python
- 3 million games for training neural networks by Álvaro Begué, CCC, February 24, 2018 » Automated Tuning
- Looking inside NNs by J. Wesley Cleveland, CCC, March 09, 2018
- GPU ANN, how to deal with host-device latencies? by Srdja Matovic, CCC, May 06, 2018 » GPU
- Poor man's neurones by Pawel Koziol, CCC, May 21, 2018 » Evaluation
- Egbb dll neural network support by Daniel Shawul, CCC, May 29, 2018 » Scorpio Bitbases
- Instruction for running Scorpio with neural network on linux by Daniel Shawul, CCC, August 01, 2018 » Scorpio
- Are draws hard to predict? by Daniel Shawul, CCC, November 27, 2018 » Draw
- use multiple neural nets? by Warren D. Smith, LCZero Forum, December 25, 2018 » Leela Chess Zero
- neural network architecture by jackd, CCC, December 26, 2018
2019
- So, how many of you are working on neural networks for chess? by Srdja Matovic, CCC, February 01, 2019
- categorical cross entropy for value by Chris Whittington, CCC, February 18, 2019
- Google's bfloat for neural networks by Srdja Matovic, CCC, April 16, 2019 » Float
- catastrophic forgetting by Daniel Shawul, CCC, May 09, 2019 » Nebiyu
- Wouldn’t it be nice if there was a ChessNet50 by Chris Whittington, CCC, July 13, 2019
- A question to MCTS + NN experts by Maksim Korzh, CCC, July 17, 2019 » Monte-Carlo Tree Search
- Re: A question to MCTS + NN experts by Daniel Shawul, CCC, July 17, 2019
- high dimensional optimization by Warren D. Smith, FishCooking, December 27, 2019 [104]
2020 ...
- How to work with batch size in neural network by Gertjan Brouwer, CCC, June 02, 2020
- NNUE accessible explanation by Martin Fierz, CCC, July 21, 2020 » NNUE
- Re: NNUE accessible explanation by Jonathan Rosenthal, CCC, July 23, 2020
- Re: NNUE accessible explanation by Jonathan Rosenthal, CCC, July 24, 2020
- LC0 vs. NNUE - some tech details... by Srdja Matovic, CCC, July 29, 2020 » Lc0
- AB search with NN on GPU... by Srdja Matovic, CCC, August 13, 2020 » GPU [105]
- Neural Networks weights type by Fabio Gobbato, CCC, August 13, 2020 » Stockfish NNUE
- Train a neural network evaluation by Fabio Gobbato, CCC, September 01, 2020 » Automated Tuning, NNUE
- Neural network quantization by Fabio Gobbato, CCC, September 08, 2020 » NNUE
- First success with neural nets by Jonathan Kreuzer, CCC, September 23, 2020
- Transhuman Chess with NN and RL... by Srdja Matovic, CCC, October 30, 2020 » RL
- Pytorch NNUE training by Gary Linscott, CCC, November 08, 2020 [106] » NNUE
- Pawn King Neural Network by Tamás Kuzmics, CCC, November 26, 2020 » NNUE
- Learning draughts evaluation functions using Keras/TensorFlow by Rein Halbersma, World Draughts Forum, November 30, 2020 » Draughts
- Maiachess by Marc-Philippe Huget, CCC, December 04, 2020 » Maia Chess
2021
- More experiments with neural nets by Jonathan Kreuzer, CCC, January 09, 2021 » Slow Chess
- Keras/Tensforflow for very sparse inputs by Jacek Dermont, CCC, January 16, 2021
- Are neural nets (the weights file) copyrightable? by Adam Treat, CCC, February 21, 2021
- A worked example of backpropagation using Javascript by Colin Jenkins, CCC, March 16, 2021 » Backpropagation
- yet another NN library by lucasart, CCC, April 11, 2021 » lucasart/nn
- Some more experiments with neural nets by Jonathan Kreuzer, CCC, June 15, 2021 » Slow Chess
- Re: Stockfish 14 has been released by Connor McMonigle, CCC, July 04, 2021 » Stockfish
- tablebase neural nets by Robert Pope, CCC, August 07, 2021 » Endgame Tablebases
- Book about Neural Networks for Chess by dkl, CCC, September 29, 2021
2022
- Binary Neural Networks Sliding Piece Inference [Release] by Daniel Infuehr, CCC, February 10, 2022 » Sliding Piece Attacks
- Failure of trivial approach to neural network move ordering by Jost Triller, CCC, February 16, 2022 » Move Ordering
External Links
- Neural network (disambiguation) from Wikipedia
- Category:Neural networks - Scholarpedia
- Neural networks - Psychology Wiki
Biological
- Biological neural network from Wikipedia
- Biological neuron model from Wikipedia
- Computational neuroscience from Wikipedia
- Neuron from Wikipedia
- Neural pathway from Wikipedia
ANNs
- Artificial neural network from Wikipedia
- Types of artificial neural networks from Wikipedia
- Artificial neural network - Wikimedia Commons
- Artificial Neural Networks - Wikibooks
- Artificial Neural Networks by Christos Stergiou and Dimitrios Siganos
- DMOZ - Computers: Artificial Intelligence: Neural Networks
- DMS Tutorial - Neural networks
- Helmholtz machine from Wikipedia
- Chess end games using Neural Networks
Topics
- Artificial neuron from Wikipedia
- Connectionism from Wikipedia
- Deep Learning from Wikipeadia
- Deep Learning - Scholarpedia by Jürgen Schmidhuber
- Feedforward neural network from Wikipedia
- Fuzzy neural network - Scholarpedia
- Generative adversarial networks from Wikipedia
- Grossberg network from Wikipedia
- Modular neural network from Wikipedia
- Neocognitron from Wikipedia
- Neocognitron - Scholarpedia by Kunihiko Fukushima
- Neural architecture search from Wikipedia
- Neuromorphic engineering from Wikipedia
- Physical neural network from Wikipedia
- Radial basis function network from Wikipedia
- Random neural network from Wikipedia
- Recursive neural network from Wikipedia
- Self-organizing map from Wikipedia
- Spiking neural network from Wikipedia
- Time delay neural network from Wikipedia
Perceptron
CNNs
- Convolutional neural network from Wikipedia
- Convolutional Neural Networks for Image and Video Processing, TUM Wiki, Technical University of Munich
- Convolutional Neural Networks
- Deep Residual Networks
- An Introduction to different Types of Convolutions in Deep Learning by Paul-Louis Pröve, July 22, 2017
- Squeeze-and-Excitation Networks by Paul-Louis Pröve, October 17, 2017
- Deep Convolutional Neural Networks by Pablo Ruiz, October 11, 2018
ResNet
- Residual neural network from Wikipedia
- Deep Residual Networks from TUM Wiki, Technical University of Munich
- Understanding and visualizing ResNets by Pablo Ruiz, October 8, 2018
RNNs
- Recurrent neural network from Wikipedia
- Recurrent neural networks - Scholarpedia
- Recurrent Neural Networks by Jürgen Schmidhuber
- Bidirectional associative memory from Wikipedia
- Boltzmann machine from Wikipedia
- Echo state network
- Hopfield network from Wikipedia
- Hopfield network - Scholarpedia
- Long short term memory from Wikipedia
Activation Functions
- Activation function from Wikipedia
- Rectifier (neural networks) from Wikipedia
- Sigmoid function from Wikipedia
- Softmax function from Wikipedia
Backpropagation
- Backpropagation from Wikipedia
- Backpropagation through structure from Wikipedia
- Backpropagation through time from Wikipedia
- Rprop from Wikipedia
- Who Invented Backpropagation? by Jürgen Schmidhuber (2014, 2015)
- A worked example of backpropagation by Alexander Schiendorfer, February 24, 2020 » Backpropagation [107]
Gradient
- Gradient from Wikipedia
- Del from Wikipedia
- Gradient descent from Wikipedia
- Conjugate gradient method from Wikipedia
- Stochastic gradient descent from Wikipedia
- ORF523: Nesterov’s Accelerated Gradient Descent by Sébastien Bubeck, I’m a bandit, April 1, 2013 » Yurii Nesterov
- Nesterov’s Accelerated Gradient Descent for Smooth and Strongly Convex Optimization by Sébastien Bubeck, I’m a bandit, March 6, 2014
- Revisiting Nesterov’s Acceleration by Sébastien Bubeck, I’m a bandit, June 30, 2015
Software
- Comparison of deep learning software from Wikipedia
- GitHub - connormcmonigle/reference-neural-network by Connor McMonigle
- GitHub - lucasart/nn: neural network experiment [108]
Libraries
- Eigen (C++ library) from Wikipedia
- Fast Artificial Neural Network Library (FANN)
- Keras from Wikipedia
- PythonForArtificialIntelligence - Python Wiki Python
- TensorFlow from Wikipedia
Blogs
- Neural Networks Blog by Ilya Sutskever
- An Introduction to Neural Networks with an Application to Games by Dean Macri, Intel Developer Zone, September 9, 2011
- John Wakefield's Dynamic Notions, a Blog about the evolution of neural networks with C# samples
- The Single Layer Perceptron
- The Sigmoid Function in C#
- Hidden Neurons and Feature Space
- Training Neural Networks Using Back Propagation in C#
- Data Mining with Artificial Neural Networks (ANN)
- Neural Net in C++ Tutorial on Vimeo (also on YouTube)
- A Gentle Introduction to Artificial Neural Networks by Dustin Stansbury, The Clever Machine, September 11, 2014
- Deep learning for… chess by Erik Bernhardsson, November 29, 2014 [109]
- Faster deep learning with GPUs and Theano by Manojit Nandi, August 05, 2015 » GPU, Python
- Enabling Continual Learning in Neural Networks by James Kirkpatrick, Joel Veness et al., DeepMind, March 13, 2017
- Understand Deep Residual Networks — a simple, modular learning framework that has redefined state-of-the-art by Michael Dietz, Waya.ai, May 02, 2017
- How to build your own AlphaZero AI using Python and Keras by David Foster, January 26, 2018 » AlphaZero, Connect Four, Python
Courses
- Machine Learning and Probabilistic Graphical Models: Course Materials - 5. Neural Networks by Sargur Srihari, University at Buffalo
- Neural Networks - Representation from Stanford Machine Learning by Andrew Ng
- Neural Networks - Learning from Stanford Machine Learning by Andrew Ng
- Neural Networks Demystified by Stephen Welch, Welch Labs
- Part 1: Data and Architecture, YouTube Videos
- Part 2: Forward Propagation
- Part 3: Gradient Descent
- Part 4: Backpropagation
- Part 5: Numerical Gradient Checking
- Part 6: Training
- Part 7: Overfitting, Testing, and Regularization
- NN - Fully Connected Tutorial, YouTube Videos by Finn Eggers
- Deep Learning Master Class by Ilya Sutskever, YouTube Video
- Lecture 10 - Neural Networks from Learning From Data - Online Course (MOOC) by Yaser Abu-Mostafa, Caltech, YouTube Video
- Lecture 12 - Learning: Neural Nets, Back Propagation by Patrick Winston, MIT, AI Lectures - Fall 2010 YouTube Videos
- Neural Networks by 3Blue1Brown, October 9, 2017, YouTube Videos [110]
- But what *is* a Neural Network? | Chapter 1
- Gradient descent, how neural networks learn | Chapter 2
- What is backpropagation really doing? | Chapter 3
- Backpropagation calculus | Appendix to Chapter 3
- Fei-Fei Li, Justin Johnson, Serena Yeung - CS231n Convolutional Neural Networks for Visual Recognition, Stanford University, 2017, YouTube Videos
- Lecture 1 | Introduction to Convolutional Neural Networks for Visual Recognition by Justin Johnson, slides
- Lecture 2 | Image Classification by Justin Johnson, slides
- Lecture 3 | Loss Functions and Optimization by Justin Johnson, slides
- Lecture 4 | Introduction to Neural Networks by Serena Yeung, slides
- Lecture 5 | Convolutional Neural Networks by Serena Yeung, slides
- Lecture 6 | Training Neural Networks I by Serena Yeung, slides
- Lecture 7 | Training Neural Networks II by Justin Johnson, slides
- Lecture 8 | Deep Learning Software by Justin Johnson, slides
- Lecture 9 | CNN Architectures by Serena Yeung, slides
- Lecture 10 | Recurrent Neural Networks by Justin Johnson, slides
- Lecture 11 | Detection and Segmentation by Justin Johnson, slides
- Lecture 12 | Visualizing and Understanding by Justin Johnson, slides
- Lecture 13 | Generative Models by Serena Yeung, slides
- Lecture 14 | Deep Reinforcement Learning by Serena Yeung, slides
- Lecture 15 | Efficient Methods and Hardware for Deep Learning by Song Han, slides
References
- ↑ An example artificial neural network with a hidden layer, Image by Colin M.L. Burnett with Inkscape, December 27, 2006, CC BY-SA 3.0, Artificial Neural Networks/Neural Network Basics - Wikibooks, Wikimedia Commons
- ↑ Biological neural network - Early study - from Wikipedia
- ↑ Warren S. McCulloch, Walter Pitts (1943). A Logical Calculus of the Ideas Immanent in Nervous Activity. Bulletin of Mathematical Biology, Vol. 5, No. 1, pdf
- ↑ Artificial neuron from Wikipedia
- ↑ The appropriate weights are applied to the inputs, and the resulting weighted sum passed to a function that produces the output y, image created by mat_the_w, based on raster image Perceptron.gif by 'Paskari', using Inkscape 0.46 for OSX, Wikimedia Commons, Perceptron from Wikipedia
- ↑ Frank Rosenblatt (1957). The Perceptron - a Perceiving and Recognizing Automaton. Report 85-460-1, Cornell Aeronautical Laboratory
- ↑ A two-layer neural network capable of calculating XOR. The numbers within the neurons represent each neuron's explicit threshold (which can be factored out so that all neurons have the same threshold, usually 1). The numbers that annotate arrows represent the weight of the inputs. This net assumes that if the threshold is not reached, zero (not -1) is output. Note that the bottom layer of inputs is not always considered a real neural network layer, Feedforward neural network from Wikipedia
- ↑ multilayer perceptron is a misnomer for a more complicated neural network
- ↑ Perceptron from Wikipedia
- ↑ Paul Werbos (1974). Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph. D. thesis, Harvard University
- ↑ Henry J. Kelley (1960). Gradient Theory of Optimal Flight Paths. [http://arc.aiaa.org/loi/arsj ARS Journal, Vol. 30, No. 10
- ↑ Arthur E. Bryson (1961). A gradient method for optimizing multi-stage allocation processes. In Proceedings of the Harvard University Symposium on digital computers and their applications
- ↑ Stuart E. Dreyfus (1961). The numerical solution of variational problems. RAND paper P-2374
- ↑ Seppo Linnainmaa (1970). The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors. Master's thesis, University of Helsinki
- ↑ Paul Werbos (1982). Applications of advances in nonlinear sensitivity analysis. System Modeling and Optimization, Springer, pdf
- ↑ Paul Werbos (1994). The Roots of Backpropagation. From Ordered Derivatives to Neural Networks and Political Forecasting. John Wiley & Sons
- ↑ Deep Learning - Scholarpedia | Backpropagation by Jürgen Schmidhuber
- ↑ Who Invented Backpropagation? by Jürgen Schmidhuber (2014, 2015)
- ↑ "Using cross-entropy error function instead of sum of squares leads to faster training and improved generalization", from Sargur Srihari, Neural Network Training (pdf)
- ↑ Yurii Nesterov from Wikipedia
- ↑ ORF523: Nesterov’s Accelerated Gradient Descent by Sébastien Bubeck, I’m a bandit, April 1, 2013
- ↑ Nesterov’s Accelerated Gradient Descent for Smooth and Strongly Convex Optimization by Sébastien Bubeck, I’m a bandit, March 6, 2014
- ↑ Revisiting Nesterov’s Acceleration by Sébastien Bubeck, I’m a bandit, June 30, 2015
- ↑ Backpropagation algorithm from Wikipedia
- ↑ PARsE | Education | GPU Cluster | Efficient mapping of the training of Convolutional Neural Networks to a CUDA-based cluster
- ↑ Ilya Sutskever, Vinod Nair (2008). Mimicking Go Experts with Convolutional Neural Networks. ICANN 2008, pdf
- ↑ Typical CNN architecture, Image by Aphex34, December 16, 2015, CC BY-SA 4.0, Wikimedia Commons
- ↑ The fundamental building block of residual networks. Figure 2 in Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun (2015). Deep Residual Learning for Image Recognition. arXiv:1512.03385
- ↑ Understand Deep Residual Networks — a simple, modular learning framework that has redefined state-of-the-art by Michael Dietz, Waya.ai, May 02, 2017
- ↑ Tristan Cazenave (2017). Residual Networks for Computer Go. IEEE Transactions on Computational Intelligence and AI in Games, Vol. PP, No. 99, pdf
- ↑ Deep Residual Networks from TUM Wiki, Technical University of Munich
- ↑ Understanding and visualizing ResNets by Pablo Ruiz, October 8, 2018
- ↑ Richard Sutton, Andrew Barto (1998). Reinforcement Learning: An Introduction. MIT Press, 11.1 TD-Gammon
- ↑ Christopher Clark, Amos Storkey (2014). Teaching Deep Convolutional Neural Networks to Play Go. arXiv:1412.3409
- ↑ Teaching Deep Convolutional Neural Networks to Play Go by Hiroshi Yamashita, The Computer-go Archives, December 14, 2014
- ↑ Why Neural Networks Look Set to Thrash the Best Human Go Players for the First Time | MIT Technology Review, December 15, 2014
- ↑ Teaching Deep Convolutional Neural Networks to Play Go by Michel Van den Bergh, CCC, December 16, 2014
- ↑ Chris J. Maddison, Aja Huang, Ilya Sutskever, David Silver (2014). Move Evaluation in Go Using Deep Convolutional Neural Networks. arXiv:1412.6564v1
- ↑ Move Evaluation in Go Using Deep Convolutional Neural Networks by Aja Huang, The Computer-go Archives, December 19, 2014
- ↑ AlphaGo | Google DeepMind
- ↑ David Silver, Aja Huang, Chris J. Maddison, Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, Sander Dieleman, Dominik Grewe, John Nham, Nal Kalchbrenner, Ilya Sutskever, Timothy Lillicrap, Madeleine Leach, Koray Kavukcuoglu, Thore Graepel, Demis Hassabis (2016). Mastering the game of Go with deep neural networks and tree search. Nature, Vol. 529
- ↑ Re: Chess program with Artificial Neural Networks (ANN)? by Gian-Carlo Pascutto, CCC, January 07, 2010
- ↑ Kieran Greer, Piyush Ojha, David A. Bell (1999). A Pattern-Oriented Approach to Move Ordering: the Chessmaps Heuristic. ICCA Journal, Vol. 22, No. 1
- ↑ Levente Kocsis, Jos Uiterwijk, Eric Postma, Jaap van den Herik (2002). The Neural MoveMap Heuristic in Chess. CG 2002
- ↑ *First release* Giraffe, a new engine based on deep learning by Matthew Lai, CCC, July 08, 2015
- ↑ Re: Deep Learning Chess Engine ? by Alexandru Mosoi, CCC, July 21, 2016
- ↑ Omid E. David, Nathan S. Netanyahu, Lior Wolf (2016). DeepChess: End-to-End Deep Neural Network for Automatic Learning in Chess. ICAAN 2016, Lecture Notes in Computer Science, Vol. 9887, Springer, pdf preprint
- ↑ David Silver, Thomas Hubert, Julian Schrittwieser, Ioannis Antonoglou, Matthew Lai, Arthur Guez, Marc Lanctot, Laurent Sifre, Dharshan Kumaran, Thore Graepel, Timothy Lillicrap, Karen Simonyan, Demis Hassabis (2017). Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. arXiv:1712.01815
- ↑ Yu Nasu (2018). ƎUИИ Efficiently Updatable Neural-Network based Evaluation Functions for Computer Shogi. Ziosoft Computer Shogi Club, pdf (Japanese with English abstract) GitHub - asdfjkl/nnue translation
- ↑ GitHub - yaneurao/YaneuraOu: YaneuraOu is the World's Strongest Shogi engine(AI player), WCSC29 1st winner, educational and USI compliant engine
- ↑ GitHub - Tama4649/Kristallweizen: 第29回世界コンピュータ将棋選手権 準優勝のKristallweizenです。
- ↑ The Stockfish of shogi by Larry Kaufman, CCC, January 07, 2020
- ↑ Stockfish NN release (NNUE) by Henk Drost, CCC, May 31, 2020
- ↑ Stockfish NNUE – The Complete Guide, June 19, 2020 (Japanese and English)
- ↑ Rosenblatt's Contributions
- ↑ The abandonment of connectionism in 1969 - Wikipedia
- ↑ Frank Rosenblatt (1962). Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms. Spartan Books
- ↑ Seppo Linnainmaa (1976). Taylor expansion of the accumulated rounding error. BIT Numerical Mathematics, Vol. 16, No. 2
- ↑ Backpropagation from Wikipedia
- ↑ Paul Werbos (1994). The Roots of Backpropagation. From Ordered Derivatives to Neural Networks and Political Forecasting. John Wiley & Sons
- ↑ Neocognitron - Scholarpedia by Kunihiko Fukushima
- ↑ Classical conditioning from Wikipedia
- ↑ Sepp Hochreiter's Fundamental Deep Learning Problem (1991) by Jürgen Schmidhuber, 2013
- ↑ Nici Schraudolph’s go networks, review by Jay Scott
- ↑ Re: Evaluation by neural network ? by Jay Scott, CCC, November 10, 1997
- ↑ Long short term memory from Wikipedia
- ↑ Tsumego from Wikipedia
- ↑ Helmholtz machine from Wikipedia
- ↑ Who introduced the term “deep learning” to the field of Machine Learning by Jürgen Schmidhuber, Google+, March 18, 2015
- ↑ Presentation for a neural net learning chess program by Dann Corbit, CCC, April 06, 2004
- ↑ Clément Farabet | Code
- ↑ Demystifying Deep Reinforcement Learning by Tambet Matiisen, Nervana, December 21, 2015
- ↑ high dimensional optimization by Warren D. Smith, FishCooking, December 27, 2019
- ↑ Generative adversarial networks from Wikipedia
- ↑ Teaching Deep Convolutional Neural Networks to Play Go by Hiroshi Yamashita, The Computer-go Archives, December 14, 2014
- ↑ Teaching Deep Convolutional Neural Networks to Play Go by Michel Van den Bergh, CCC, December 16, 2014
- ↑ Arasan 19.2 by Jon Dart, CCC, November 03, 2016 » Arasan's Tuning
- ↑ GitHub - BarakOshri/ConvChess: Predicting Moves in Chess Using Convolutional Neural Networks
- ↑ ConvChess CNN by Brian Richardson, CCC, March 15, 2017
- ↑ Jürgen Schmidhuber (2015) Critique of Paper by "Deep Learning Conspiracy" (Nature 521 p 436).
- ↑ How Facebook’s AI Researchers Built a Game-Changing Go Engine | MIT Technology Review, December 04, 2015
- ↑ Combining Neural Networks and Search techniques (GO) by Michael Babigian, CCC, December 08, 2015
- ↑ DeepChess: Another deep-learning based chess program by Matthew Lai, CCC, October 17, 2016
- ↑ ICANN 2016 | Recipients of the best paper awards
- ↑ Jigsaw puzzle from Wikipedia
- ↑ CMA-ES from Wikipedia
- ↑ Re: Minic version 3 by Connor McMonigle, CCC, November 03, 2020 » Minic 3, Seer 1.1
- ↑ catastrophic forgetting by Daniel Shawul, CCC, May 09, 2019
- ↑ Using GAN to play chess by Evgeniy Zheltonozhskiy, CCC, February 23, 2017
- ↑ GitHub - paintception/DeepChess
- ↑ AlphaGo Zero: Learning from scratch by Demis Hassabis and David Silver, DeepMind, October 18, 2017
- ↑ Google's AlphaGo team has been working on chess by Peter Kappler, CCC, December 06, 2017
- ↑ Residual Networks for Computer Go by Brahim Hamadicharef, CCC, December 07, 2017
- ↑ Translation of Yu Nasu's NNUE paper by Dominik Klein, CCC, January 07, 2021
- ↑ AlphaZero: Shedding new light on the grand games of chess, shogi and Go by David Silver, Thomas Hubert, Julian Schrittwieser and Demis Hassabis, DeepMind, December 03, 2018
- ↑ Book about Neural Networks for Chess by dkl, CCC, September 29, 2021
- ↑ Acquisition of Chess Knowledge in AlphaZero, ChessBase News, November 18, 2021
- ↑ Alois Heinz (1994). Efficient Neural Net α-β-Evaluators. pdf
- ↑ Mathieu Autonès, Aryel Beck, Phillippe Camacho, Nicolas Lassabe, Hervé Luga, François Scharffe (2004). Evaluation of Chess Position by Modular Neural network Generated by Genetic Algorithm. EuroGP 2004
- ↑ Naive Bayes classifier from Wikipedia
- ↑ GitHub - pluskid/Mocha.jl: Deep Learning framework for Julia
- ↑ Rectifier (neural networks) from Wikipedia
- ↑ Muthuraman Chidambaram, Yanjun Qi (2017). Style Transfer Generative Adversarial Networks: Learning to Play Chess Differently. arXiv:1702.06762v1
- ↑ Yann Dauphin, Razvan Pascanu, Caglar Gulcehre, Kyunghyun Cho, Surya Ganguli, Yoshua Bengio (2014). Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. arXiv:1406.2572
- ↑ kernel launch latency - CUDA / CUDA Programming and Performance - NVIDIA Developer Forums by LukeCuda, June 18, 2018
- ↑ PyTorch from Wikipedia
- ↑ A worked example of backpropagation using Javascript by Colin Jenkins, CCC, March 16, 2021
- ↑ yet another NN library by lucasart, CCC, April 11, 2021
- ↑ erikbern/deep-pink · GitHub
- ↑ Neural networks (NN) explained by Erin Dame, CCC, December 20, 2017