Alpha-Beta

The Alpha-Beta algorithm (Alpha-Beta Pruning, Alpha-Beta Heuristic [2] ) is a significant enhancement to the minimax search algorithm that eliminates the need to search large portions of the game tree applying a branch-and-bound technique. Remarkably, it does this without any potential of overlooking a better move. If one already has found a quite good move and search for alternatives, one refutation is enough to avoid it. No need to look for even stronger refutations. The algorithm maintains two values, alpha and beta. They represent the minimum score that the maximizing player is assured of and the maximum score that the minimizing player is assured of respectively. Consider the following example...
Contents
How it works
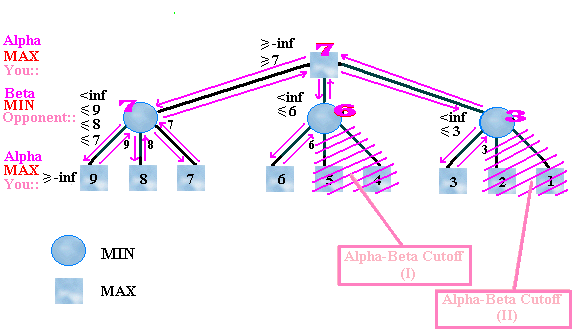
Say it is White's turn to move, and we are searching to a depth of 2 (that is, we are consider all of White's moves, and all of Black's responses to each of those moves.) First we pick one of White's possible moves - let's call this Possible Move #1. We consider this move and every possible response to this move by black. After this analysis, we determine that the result of making Possible Move #1 is an even position. Then, we move on and consider another of White's possible moves (Possible Move #2.) When we consider the first possible counter-move by black, we discover that playing this results in black winning a Rook! In this situation, we can safely ignore all of Black's other possible responses to Possible Move #2 because we already know that Possible Move #1 is better. We really don't care exactly how much worse Possible Move #2 is. Maybe another possible response wins a Queen, but it doesn't matter because we know that we can achieve at least an even game by playing Possible Move #1. The full analysis of Possible Move #1 gave us a lower bound. We know that we can achieve at least that, so anything that is clearly worse can be ignored.
The situation becomes even more complicated, however, when we go to a search depth of 3 or greater, because now both players can make choices affecting the game tree. Now we have to maintain both a lower bound and an upper bound (called Alpha and Beta.) We maintain a lower bound because if a move is too bad we don't consider it. But we also have to maintain an upper bound because if a move at depth 3 or higher leads to a continuation that is too good, the other player won't allow it, because there was a better move higher up on the game tree that he could have played to avoid this situation. One player's lower bound is the other player's upper bound.
Savings
The savings of alpha beta can be considerable. If a standard minimax search tree has x nodes, an alpha beta tree in a well-written program can have a node count close to the square-root of x. How many nodes you can actually cut, however, depends on how well ordered your game tree is. If you always search the best possible move first, you eliminate the most of the nodes. Of course, we don't always know what the best move is, or we wouldn't have to search in the first place. Conversely, if we always searched worse moves before the better moves, we wouldn't be able to cut any part of the tree at all! For this reason, good move ordering is very important, and is the focus of a lot of the effort of writing a good chess program. As pointed out by Levin in 1961, assuming constantly b moves for each node visited and search depth n, the maximal number of leaves in alpha-beta is equivalent to minimax, b ^ n. Considering always the best move first, it is b ^ ceil(n/2) plus b ^ floor(n/2) minus one. The minimal number of leaves is shown in following table which also demonstrates the odd-even effect:
| depth n | bn | b⌈n/2⌉ + b⌊n/2⌋ - 1 |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 40 | 40 |
| 2 | 1,600 | 79 |
| 3 | 64,000 | 1,639 |
| 4 | 2,560,000 | 3,199 |
| 5 | 102,400,000 | 65,569 |
| 6 | 4,096,000,000 | 127,999 |
| 7 | 163,840,000,000 | 2,623,999 |
| 8 | 6,553,600,000,000 | 5,119,999 |
History
Alpha-Beta was invented independently by several researchers and pioneers from the 50s [3], and further research until the 80s, most notable by
- John McCarthy proposed the idea of Alpha-Beta after the representation of the Chess Program by Alex Bernstein [4] at the Dartmouth Workshop in 1956 [5]
- Allen Newell and Herbert Simon Approximation in 1958
- Arthur Samuel Approximation in 1959
- Daniel Edwards and Timothy Hart, Description in 1961 [6]
- Alexander Brudno, Description in 1963
- Samuel Fuller, John Gaschnig, James Gillogly, Analysis 1973 [7]
- Donald Knuth, Analysis in 1975
- Knuth and Moore‘s famous Function F2, aka AlphaBeta
- Knuth already introduced an iterative solution, see Iterative Search
- Knuth's node types
- Gérard M. Baudet, Analysis in 1978
Quotes
McCarthy
Quote by John McCarthy from Human-Level AI is harder than it seemed in 1955 on the Dartmouth workshop:
Chess programs catch some of the human chess playing abilities but rely on the limited effective branching of the chess move tree. The ideas that work for chess are inadequate for go. Alpha-beta pruning characterizes human play, but it wasn't noticed by early chess programmers - Turing, Shannon, Pasta and Ulam, and Bernstein. We humans are not very good at identifying the heuristics we ourselves use. Approximations to alpha-beta used by Samuel, Newell and Simon, McCarthy. Proved equivalent to minimax by Hart and Levin, independently by Brudno. Knuth gives details.
Ershov and Shura-Bura
Quote from The Early Development of Programming in the USSR by Andrey Ershov and Mikhail R. Shura-Bura [8]
At the end of the 1950's a group of Moscow mathematicians began a study of computerized chess. Sixteen years later, the studies would lead to victory in the first world chess tournament for computer programs held in Stockholm during the 1974 IFIP Congress. An important component of this success was a deep study of the problems of information organization in computer memory and of various search heuristics. G. M. Adelson-Velsky and E. M. Landis invented the binary search tree ("dichotomic inquiry") and A. L. Brudno, independent of J. McCarthy, discovered the (α,β)-heuristic for reducing search times on a game tree.
Knuth
Quote by Knuth [9] : It is interesting to convert this recursive procedure to an iterative (non-recursive) form by a sequence of mechanical transformations, and to apply simple optimizations which preserve program correctness. The resulting procedure is surprisingly simple, but not as easy to prove correct as the recursive form.
Implementation
Max versus Min
A C-like pseudo code implementation of the alpha-beta algorithm with distinct indirect recursive routines for the max- and min-player, similar to the minimax routines. Making and unmaking moves is omitted, and should be done before and after the recursive calls. So called beta-cutoffs occur for the max-play, alpha-cutoffs for the min-player.
int alphaBetaMax( int alpha, int beta, int depthleft ) {
if ( depthleft == 0 ) return evaluate();
for ( all moves) {
score = alphaBetaMin( alpha, beta, depthleft - 1 );
if( score >= beta )
return beta; // fail hard beta-cutoff
if( score > alpha )
alpha = score; // alpha acts like max in MiniMax
}
return alpha;
}
int alphaBetaMin( int alpha, int beta, int depthleft ) {
if ( depthleft == 0 ) return -evaluate();
for ( all moves) {
score = alphaBetaMax( alpha, beta, depthleft - 1 );
if( score <= alpha )
return alpha; // fail hard alpha-cutoff
if( score < beta )
beta = score; // beta acts like min in MiniMax
}
return beta;
}
With this call from the Root:
score = alphaBetaMax(-oo, +oo, depth);
Alpha-beta search tree with two alpha-cuts at min nodes [10]
Negamax Framework
Inside a negamax framework the routine looks simpler, but is not necessarily simpler to understand. Despite negating the returned score of the direct recursion, alpha of the min-player becomes minus beta of the max-player and vice versa, and the term alpha-cutoff or alpha-pruning is somehow diminished.
int alphaBeta( int alpha, int beta, int depthleft ) {
if( depthleft == 0 ) return quiesce( alpha, beta );
for ( all moves) {
score = -alphaBeta( -beta, -alpha, depthleft - 1 );
if( score >= beta )
return beta; // fail hard beta-cutoff
if( score > alpha )
alpha = score; // alpha acts like max in MiniMax
}
return alpha;
}
Note #1: Notice the call to quiesce(). This performs a quiescence search, which makes the alpha-beta search much more stable.
Note #2: This function only returns the score for the position, not the best move. Normally, a different (but very similar) function is used for searching the root node. The SearchRoot function calls the alphaBeta function and returns both a score and a best move. Also, most search functions collect the Principal Variation not only for display purposes, but for a good guess as the leftmost path of the next iteration inside an iterative deepening framework.
Fail hard
Since alpha and beta act as hard bounds of the return value if depth left is greater zero in the above code samples, this is referred to a fail-hard-framework.
Outside the Bounds
Fail-Soft Alpha-Beta [11] may return scores outside the bounds, that is either greater than beta or less than alpha. It has to keep track of the best score, which might be below alpha.
int alphaBeta( int alpha, int beta, int depthleft ) {
int bestscore = -oo;
if( depthleft == 0 ) return quiesce( alpha, beta );
for ( all moves) {
score = -alphaBeta( -beta, -alpha, depthleft - 1 );
if( score >= beta )
return score; // fail-soft beta-cutoff
if( score > bestscore ) {
bestscore = score;
if( score > alpha )
alpha = score;
}
}
return bestscore;
}
Enhancements
The alpha-beta algorithm can also be improved. These enhancements come from the fact that if you restrict the window of scores that are interesting, you can achieve more cutoffs. Since move ordering is so much important, a technique applied outside of the search for this is iterative deepening boosted by a transposition table, and possibly aspiration windows. Other enhancements, applied within the search function, are further discussed.
Obligatory
Selectivity
Scout and Friends
Alpha-Beta goes Best-First
See also
- Alpha
- Alpha-Beta Benchmark by Stephen F. Wheeler
- Beta
- Beta-Cutoff
- Bound
- CPW-Engine_search
- Fail-Low
- Fail-High
- Gamma-Algorithm
- Iterative Search
- KC Chess
- MCαβ
- Minimax
- Negamax
- Node Types
- Odd-Even Effect
- Parallel Alpha-Beta
Selected Publications
1958 ..
- Allen Newell, Cliff Shaw, Herbert Simon (1958). Chess Playing Programs and the Problem of Complexity. IBM Journal of Research and Development, Vol. 4, No. 2, pp. 320-335. Reprinted (1963) in Computers and Thought (eds. Edward A. Feigenbaum and Julian Feldman), pp. 39-70. McGraw-Hill, New York, N.Y., pdf
- Arthur Samuel (1959). Some Studies in Machine Learning Using the Game of Checkers. IBM Journal July 1959
1960 ...
- Daniel Edwards, Timothy Hart (1961). The Alpha-Beta Heuristic, AIM-030, reprint available from DSpace at MIT. Retrieved on 2006-12-21.
- Alexander Brudno (1963). Bounds and valuations for shortening the search of estimates. Problemy Kibernetiki (10) 141–150 and Problems of Cybernetics (10) 225–241
- James R. Slagle (1963). Game Trees, M & N Minimaxing, and the M & N alpha-beta procedure. Artificial Intelligence Group Report 3, UCRL-4671, University of California
- James R. Slagle, John K. Dixon (1969). Experiments With Some Programs That Search Game Trees. Journal of the ACM, Vol. 16, No. 2: 189-207, pdf
1970 ...
- Samuel Fuller, John Gaschnig, James Gillogly (1973). An Analysis of the Alpha-Beta Pruning Algorithm. Technical Report, Carnegie Mellon University, pdf
- Donald Knuth, Ronald W. Moore (1975). An Analysis of Alpha-Beta Pruning. Artificial Intelligence, Vol. 6, No. 4, pp 293–326. Reprinted in Donald Knuth (2000). Selected Papers on Analysis of Algorithms. CSLI lecture notes series 102, ISBN 1-57586-212-3, pdf
- Arnold K. Griffith (1976). Empirical Exploration of the Performance of the Alpha-Beta Tree-Searching Heuristic. IEEE Transactions on Computers, Vol. C-25, No. 1
- Gérard M. Baudet (1978). An Analysis of the Full Alpha-Beta Pruning Algorithm. STOC 1978: 296-313
- Gérard M. Baudet (1978). On the branching factor of the alpha-beta pruning algorithm. Artificial Intelligence, Vol. 10
- Patrick Winston (1978). Dealing with Adversaries. Personal Computing, Vol. 2, No. 11, pp. 30, November 1978 » Alpha-Beta
- Gary Lindstrom (1979). Alpha-Beta Pruning on Evolving Game Trees. Technical Report UUCCS 79-101, University of Utah, UScholar Works
- Ward Douglas Maurer (1979). Alpha-Beta Pruning. BYTE, Vol. 4, No. 11, pp. 84-96
1980 ...
- David Levy (1980). Intelligent Games. Creative Computing, Vol. 6, No. 4, hosted by the Internet Archive
- Judea Pearl (1981). Heuristic search theory: A survey of recent results. IJCAI-81, pdf
- Igor Roizen (1981). On the Average Number of Terminal Nodes examined by Alpha-Beta. Technical Report UCLA-ENG-CSL-8108, University of California at Los Angeles, Cognitive Systems Laboratory
- Judea Pearl (1982). The Solution for the Branching Factor of the Alpha-Beta Pruning Algorithm and its Optimality. Communications of the ACM, Vol. 25, No. 8
- Peter W. Frey (1983). The Alpha-Beta Algorithm: Incremental Updating, Well-Behaved Evaluation Functions, and Non-Speculative Forward Pruning. Computer Game-Playing (ed. Max Bramer), pp. 285-289. Ellis Horwood Limited
- John Philip Fishburn (1983). Another optimization of alpha-beta search. SIGART Bulletin, Issue 84, pdf » Fail-Soft
- John Hughes (1984). Why Functional Programming Matters. 5 An Example from Artificial Intelligence, Chalmers Tekniska Högskola, Göteborg, pdf,
- Stephen F. Wheeler (1985). A performance benchmark of the alpha-beta procedure on randomly ordered non-uniform depth-first game-trees generated by a chess program. M.Sc. thesis, East Texas State University
- Toshihide Ibaraki (1986). Generalization of Alpha-Beta and SSS* Search Procedures. Artificial Intelligence, Vol. 29
- Matthew Huntbach, F. Warren Burton (1988). Alpha-beta search on virtual tree machines. Information Sciences, Vol. 44, No. 1
- Robert Hyatt, Bruce W. Suter, Harry Nelson (1989). A Parallel Alpha-Beta Tree Searching Algorithm. Parallel Computing, Vol. 10, No. 3
1990 ...
- Ingo Althöfer, Bernhard Balkenhol (1991). A Game Tree with Distinct Leaf Values which is Easy for the Alpha-Beta Algorithm. Artificial Intelligence Vol. 52, No. 2
- Alois Heinz, Christoph Hense (1993). Bootstrap learning of α-β-evaluation functions. ICCI 1993, pdf
- Van-Dat Cung (1993). Parallelizations of Game-Tree Search. PARCO 1993, pdf hosted by CiteSeerX
- Alois Heinz (1994). Efficient Neural Net α-β-Evaluators. pdf
- Yanjun Zhang (1995). On the Optimality of Randomized Alpha-Beta Search. SIAM Journal on Computing, Vol. 24, No. 1
- Ernst A. Heinz (1999). Scalable Search in Computer Chess. Morgan Kaufmann, ISBN 3-528-05732-7
2000 ...
- Matthew L. Ginsberg, Alan Jaffray (2002). Alpha-Beta Pruning Under Partial Orders. in Richard J. Nowakowski (ed.) More Games of No Chance. Cambridge University Press, pdf
- Todd W. Neller (2002). Information-Based Alpha-Beta Search and the Homicidal Chauffeur. HSCC 2002, in Claire J. Tomlin, Mark R. Greenstreet (eds.) (2002). Hybrid Systems: Computation and Control. Lecture Notes in Computer Science 2289, Springer [12]
- Jacek Mańdziuk, Daniel Osman (2004). Alpha-Beta Search Enhancements with a Real-Value Game-State Evaluation Function. ICGA Journal, Vol. 27, No. 1, pdf
- Hendrik Baier (2006). Der Alpha-Beta-Algorithmus und Erweiterungen bei Vier Gewinnt. Bachelor's thesis (German), TU Darmstadt, advisor Johannes Fürnkranz, pdf
2010 ...
- Damjan Strnad, Nikola Guid (2011). Parallel Alpha-Beta Algorithm on the GPU. CIT. Journal of Computing and Information Technology, Vol. 19, No. 4 » GPU, Parallel Search, Reversi
- Abdallah Saffidine, Hilmar Finnsson, Michael Buro (2012). Alpha-Beta Pruning for Games with Simultaneous Moves. AAAI 2012
- Daniel S. Abdi (2013). Analysis of pruned minimax trees. pdf » Late Move Reductions, Null Move Pruning
- Jr-Chang Chen, I-Chen Wu, Wen-Jie Tseng, Bo-Han Lin, Chia-Hui Chang (2015). Job-Level Alpha-Beta Search. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 7, No. 1
- Bojun Huang (2015). Pruning Game Tree by Rollouts. AAAI » MCTS, MT-SSS*, Rollout Paradigm [13]
- Naoyuki Sato, Kokolo Ikeda (2016). Three types of forward pruning techniques to apply the alpha beta algorithm to turn-based strategy games. CIG 2016
- Hendrik Baier (2017). A Rollout-Based Search Algorithm Unifying MCTS and Alpha-Beta. Computer Games » MCαβ, Monte-Carlo Tree Search
- Shogo Takeuchi (2019). Advice is Useful for Game AI: Experiments with Alpha-Beta Search Players in Shogi. Advances in Computer Games 16
Forum Posts
1993 ...
- computer chess by Paul W Celmer, rgc, September 10, 1993
- Re: Computer Chess (LONG) by Andy Walker, rgc, September 16, 1993
- Computer Chess and alpha-beta pruning by Rickard Westman, rgc, September 21, 1993
- Re: Computer Chess and alpha-beta pruning by Johannes Fürnkranz, rgc, September 22, 1993 » Iterative Deepening
- alpha-beta pruning != brute force by Feng-hsiung Hsu, rgc, September 22, 1993 » Brute-Force
- Re: Computer Chess and alpha-beta pruning by Robert Hyatt, rgc, September 25, 1993
- Alpha-beta inconsistencies by Chua Kong Sian, rgc, February 19, 1994
1995 ...
- Alpha-Beta explained? by Brian, rgcc, October 15, 1996
- New improvement to alpha/beta + TT? by Heiner Marxen, rgcc, January 13, 1997 » Fail-Soft
- Re: Argument against Alpha-Beta searching by Robert Hyatt, rgcc, March 19, 1997
- computer chess "oracle" ideas... by Robert Hyatt, rgcc, April 1, 1997 » Oracle
- Re: computer chess "oracle" ideas... by Ronald de Man, rgcc, April 3, 1997
- Re: computer chess "oracle" ideas... by Ronald de Man, rgcc, April 7, 1997
- Basic alpha-beta question by John Scalo, CCC, January 06, 1998
- alpha-beta is silly? by Werner Inmann, CCC, June 02, 1998
- Re: alpha-beta is silly? by Don Dailey, CCC, June 03, 1998
- Re: Basic questions about alpha beta by Bruce Moreland, CCC, September 28, 1998
2000 ...
- Another Alpha-Beta algorithm question by Jeff Anderson, CCC, February 18, 2000
- A Question on simple Alpha-Beta versus PVS/Negascout by Andrei Fortuna, CCC, March 21, 2000 » Principal Variation Search, NegaScout
- outline for alpha beta by John Coffey, CCC, May 12, 2000
- Alpha-Beta explanation on Heinz's book? by Severi Salminen, CCC, October 05, 2000 [14]
- Who invented the Alpha-Beta-algorithm? by Rafael B. Andrist, CCC, April 09, 2001
- The Alpha-Beta search! by Sune Fischer, CCC, August 14, 2001
- An Idiot's Guide to Minimax, Alpha/Beta, etc... by Mike Carter, CCC, February 03, 2003
- Fail soft alpha-beta by Russell Reagan, CCC, September 08, 2003 » Fail-Soft
- Complexity Analyses of Alpha-Beta by Renze Steenhuisen, CCC, October 07, 2003
- Mixing alpha-beta with PN search by Tord Romstad, CCC, January 18, 2004 » Proof-Number Search
- Question for Hyatt about Alpha/Beta by Bob Durrett, CCC, February 05, 2004
2005 ...
- Iterative alpha-beta search? by Andrew Wagner, CCC, January 11, 2006 » Iterative Search
- Trivial alfa-beta question by Jouni Uski, CCC, February 18, 2006
2010 ...
- Dumb question about alpha-beta by Daylen Yang, CCC, March 04, 2014
2015 ...
- Search algorithm in it's simplest forum by Mahmoud Uthman, CCC, February 25, 2015
- Negative alpha/beta windows: Are they useful? by Thomas Dybdahl Ahle, CCC, March 06, 2015
- Stuck on Alphabeta by kuket15, OpenChess Forum, December 07, 2015
- Alpha-Beta woes, textbook-like resources, etc. by Meni Rosenfeld, CCC, January 14, 2016
- Search by Laurie Tunnicliffe, CCC, June 24, 2016
- Alpha-Beta as a rollouts algorithm by Daniel Shawul, CCC, January 25, 2018 » MCαβ, Monte-Carlo Tree Search, Scorpio
2020 ...
- AB search with NN on GPU... by Srdja Matovic, CCC, August 13, 2020 » GPU, NN [15]
- Mathematical proof that AB with B-cutoff does not miss a variation by Yves De Billoëz, CCC, April 30, 2021
- Alpha-beta search for drawing endgames by Emanuel Torres, CCC, June 16, 2021 » Draw Evaluation, Graph History Interaction, Repetitions
External Links
- Alpha-beta Pruning from Wikipedia
- Branch-and-bound from Wikipedia
- Integer programming from Wikipedia [16]
- The alpha-beta heuristic from Alex Bell (1972). Games Playing with Computers. Allen & Unwin, ISBN-13: 978-0080212227
- Alpha-Beta Search from Bruce Moreland's Programming Topics
- Lecture notes for April 22, 1997 Alpha-Beta Search by David Eppstein
- G13GAM -- Game Theory - alpha-beta pruning by Andy Walker (Wayback Machine)
- Alpha-Beta from How Rebel Plays Chess by Ed Schröder (Wayback Machine)
- Alpha-Beta search from Paul Verhelst's Computer Chess Sites (Wayback Machine)
- Alpha-Beta Slide Show in 18 steps by Mikael Bodén
- An Introduction to Game Tree Algorithms by Hamed Ahmadi
- Alpha Beta - Astral Abuse, 1971, YouTube Video
- Alpha Beta are Vilma Lado, Vangelis Papathanassiou, Argyris Koulouris and Giorgio Gomelski
References
- ↑ Alpha Beta - Astral Abuse a look at the music of Vangelis Papathanassiou
- ↑ Arthur Samuel (1967). Some Studies in Machine Learning. Using the Game of Checkers. II-Recent Progress. pdf, IBM Journal - November 1967, on the name Alpha-Beta Heuristic pp. 602: So named by Prof. John McCarthy. This procedure was extensively investigated by Prof. John McCarthy and his students at M.I.T. but it has been inadequately described in the literature. It is, of course, not a heuristic at all, being a simple algorithmic procedure and actually only a special case of the more general "branch and bound" technique which was been rediscovered many times and which is currently being exploited in integer programming research.
- ↑ Jaap van den Herik (2001). Science, Competition and Business. ICGA Journal, Vol. 24, No. 4, pdf
- ↑ The Dartmouth Workshop--as planned and as it happened
- ↑ A Proposal for the Dartmouth Summer Research Project on Artificial Intelligence by John McCarthy, Marvin Minsky, Nathaniel Rochester, Claude Shannon, August 31, 1955
- ↑ Daniel Edwards and Timothy Hart (1961). The Alpha-Beta Heuristic, AIM-030, reprint available from DSpace at MIT. Retrieved on 2006-12-21.
- ↑ Samuel Fuller, John Gaschnig, James Gillogly (1973). An Analysis of the Alpha-Beta Pruning Algorithm. Technical Report, Carnegie Mellon University
- ↑ Andrey Ershov, Mikhail R. Shura-Bura (1980). The Early Development of Programming in the USSR. in Nicholas C. Metropolis (ed.) A History of Computing in the Twentieth Century. Academic Press, preprint pp. 44
- ↑ Donald Knuth, Ronald W. Moore (1975). An analysis of alpha-beta pruning. Artificial Intelligence, Vol. 6, No. 4, pp 293–326. Reprinted in Donald Knuth (2000). Selected Papers on Analysis of Algorithms. CSLI lecture notes series 102, ISBN 1-57586-212-3
- ↑ McGill University, Winter 1997 Class Notes, Topic #11: Game trees. Alpha-beta search, Diagram by Pui Yee Chan
- ↑ John Philip Fishburn (1983). Another optimization of alpha-beta search. SIGART Bulletin, Issue 84
- ↑ Homicidal chauffeur problem - Wikipedia
- ↑ Re: Announcing lczero by Daniel Shawul, CCC, January 21, 2018 » Leela Chess Zero
- ↑ Ernst A. Heinz (1999). Scalable Search in Computer Chess. Morgan Kaufmann, ISBN 3-528-05732-7
- ↑ kernel launch latency - CUDA / CUDA Programming and Performance - NVIDIA Developer Forums by LukeCuda, June 18, 2018
- ↑ William Cook (2009). Fifty-Plus Years of Combinatorial Integer Programming. pdf