Proof-Number Search
Home * Search * Proof-Number Search
Proof-Number Search, (Pn-Search, PnS, PNS)
a best-first and-or tree search algorithm designed by Victor Allis for finding the game-theoretical value in game trees [2] . PNS is based on ideas derived from conspiracy number search. While in cn search the purpose is to continue searching until it is unlikely that the minimax value of the root will change, PNS aims at proving the true value of the root [3]. In the fall 2012 issue of the ICGA Journal, about 20 years after its invention, Akihiro Kishimoto, Mark Winands, Martin Müller and Jahn-Takeshi Saito wrote a résumé about PNS and its variants and enhancements, considered a tribute to Victor Allis by editor Jaap van den Herik [4] [5] .
Contents
Algorithm
Conspiracy Numbers
PNS specializes conspiracy numbers to and-or tree search with binary outcome, with significant reduced memory requirements compared to CnS [6] . MAX-nodes are represented as OR-nodes, MIN-nodes as AND-nodes. A solved tree with value true is called proved, while a solved tree with value false is called disproved. Evaluation of leaves yields in the values of false, true or unknown, the latter can be expanded to become a frontier node. For backpropagation, after expansion, AND-nodes become false if at least one child is false, else unknown if at least one child is unknown, otherwise true. At OR-nodes, false and true are interchanged analogously.
Proof and Disproof Numbers
The algorithm requires the whole tree in memory to select the next evaluated but yet unknown node to be expanded using two criteria: the potential range of subtree values and the number of nodes which must conspire to prove or disprove that range of potential values. These two criteria enable PNS to treat game trees with a non-uniform branching factor and deep and narrow lines efficiently.
PNS continuously tries to solve the tree by focusing on the potentially shortest solution, i.e., consisting of the least number of nodes. At each step of the search, a node which is part of the potentially shortest solution available is selected and expanded or developed. After expansion, its conspiracy numbers, the proof- and disproof number, are established anew, to update the proof- and disproof numbers of its ancestors. This process of selection, expansion and ancestor update is repeated until either the tree is solved or has run out of time- or memory resources.
Tree Sample
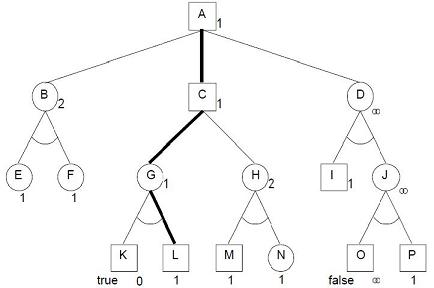
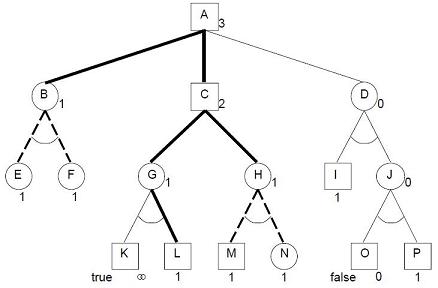
Following sample, taken from Allis' Ph.D. thesis [7] , illustrates how proof and disproof numbers are assigned and updated to solve the tree.
All frontier nodes (E, F, I, L, M, N and P) have proof number or conspiracy of 1. A terminal node with value true (node K) has proof number 0, with value false (node O), proof number ∞. Internal AND-nodes (B, D, G, H and J) have proof numbers equal to the sum of the proof numbers of their children, internal OR-nodes (A and C) have proof numbers equal to the minimum of the proof numbers of their children. Disproof numbers behave analogously to proof numbers, interchanging the roles of AND-nodes and OR-nodes, and the cardinalities 0 and ∞. Each pair consisting of a smallest proof set and a smallest disproof set has a non-empty intersection.
| And-or tree with proof numbers | and disproof numbers |
Pseudo Code
The PNS C-like pseudo code is based on the code given in Game-Tree Search using Proof Numbers: The First Twenty Years by Kishimoto et al. [8] . The domain dependent procedure evaluate assigns one of the values proven, disproven and unknown to node.value.
void PNS ( Node root ) {
evaluate( root );
setProofAndDisproofNumbers( root );
Node current = root;
while ( root.proof != 0 && root.disproof != 0 && resourcesAvailable() ) {
Node mostProving = selectMostProvingNode( current );
expandNode( mostProving );
current = updateAncestors( mostProving, root );
}
}
Set Numbers
void setProofAndDisproofNumbers( Node n ) {
if ( n.expanded ) { /* interior node */
if ( n.type == AND ) {
n.proof = 0; n.disproof = ∞;
for (each child c of n) {
n.proof += c.proof;
n.disproof = min(n.disproof, c.disproof);
}
} else { /* OR node */
n.proof = ∞; n.disproof = 0;
for (each child c of n) {
n.disproof += c.disproof;
n.proof = min(n.proof, c.proof);
}
}
} else { /* terminal node or none terminal leaf */
switch( n.value ) {
case disproven: n.proof = ∞; n.disproof = 0; break;
case proven: n.proof = 0; n.disproof = ∞; break;
case unknown: n.proof = 1; n.disproof = 1; break;
}
}
}
Select
Node selectMostProvingNode( Node n ) {
while ( n.expanded ) {
int value = ∞;
Node best;
if ( n.type == AND ) {
for (each child c of n) {
if ( value > c.disproof ) {
best = c;
value = c.disproof;
}
}
} else { /* OR node */
for (each child c of n) {
if ( value > c.proof ) {
best = c;
value = c.proof;
}
}
}
n = best;
}
return n;
}
Expand
void expandNode( Node n ) {
generateChildren( n );
for (each child c of n) {
evaluate( c );
setProofAndDisproofNumbers( c );
if ( n.type == AND ) {
if ( c.disproof == 0 ) break;
} else { /* OR node */
if ( c.proof == 0 ) break;
}
}
n.expanded = true;
}
Update Ancestors
Node updateAncestors( Node n, Node root ) {
while( n != root ) {
int oldProof = n.proof;
int oldDisproof = n.disproof;
setProofAndDisproofNumbers( n );
if ( n.proof == oldProof && n.disproof == oldDisproof )
return n;
n = n.parent;
}
setProofAndDisproofNumbers( root );
return root;
}
Enhancements
Proof-number search as illustrated above is suited for pure trees, but has issues with games consisting of directed acyclic graphs (transpositions) and even more, directed cyclic graphs (repetitions), already addressed by Martin Schijf in 1993 [9] .
Pn²
The Pn² search algorithm safes resources by using a second PNS instead of calling evaluate, which child-nodes can be discarded afterwards [10] .
Depth First
C* and PN*, introduced by Masahiro Seo [11] and Seo et al [12] , transforms a best-first PNS into an iterative deepening depth-first approach df-pn. Moreover, PN* also incorporates ideas from Korf's Linear-Space Best-First Search (RBFS) [13], and is enhanced by methods such as recursive iterative deepening, dynamic evaluation, efficient successor ordering, and pruning by dependency relations.
PDS
Ayumu Nagai proposed a depth-first variation of PNS dubbed PDS for Proof-number and Disproof-number Search [14] .
PDS-PN
PDS-PN is a two-level search, which performs a depth-first Proof-number and Disproof-number Search (PDS) at the first level, followed by second level best-first PNS [15] .
Parallel PNS
Parallel search implementations of PNS were introduced by Akihiro Kishimoto and Yoshiyuki Kotani in 1999 [16] , and by Tomoyuki Kaneko in 2010 [17] .
Applications
In conjunction with retrograde analysis and alpha-beta, PNS approaches were used to solve various games completely or partial, and to support game playing programs in finding game theoretic solutions. As pointed out by Kishimoto et al. [18] , Victor Allis first used the notion of proof and disproof numbers while analyzing and solving Connect Four, still called conspiracy numbers [19] . Charles Elkan applied proof numbers to theorem proving [20] . In Go, PNS could be applied in Life and death situations [21] , and PNS played an important role in solving Checkers by Jonathan Schaeffer et al. in 2007 [22] [23] .
In Shogi as well in Chess, PNS solves deep tsume-shogi or mate problems. Prover was a PNS implementation for chess, using chess-specific routines of Duck. Provers only goal was searching for mate [24] . Sjeng by Gian-Carlo Pascutto uses Proof-number search in it's suicide and loser's mode [25] .
See also
- Conspiracy Numbers
- Conspiracy Number Search
- Lambda-Search
- Mate Search
- Retrograde Analysis
- Theorem-Proving by James R. Slagle
- Theorem-Proving from Five-Year Plan by Jack Good
Publications
1988 ...
- Victor Allis (1988). A Knowledge-Based Approach of Connect Four: The Game is Over, White to Move Wins. M.Sc. thesis, Report No. IR-163, Faculty of Mathematics and Computer Science, Vrije Universteit, Amsterdam
- Charles Elkan (1989). Conspiracy Numbers and Caching for Searching And/Or Trees and Theorem-Proving. IJCAI 1989, pdf
1990 ...
- Victor Allis, Maarten van der Meulen, Jaap van den Herik (1991). Proof-Number Search. Technical Reports in Computer Science, CS 91-01. Department of Computer Science, University of Limburg. ISSN 0922-8721.
- Victor Allis, Patrick Schoo (1992). Qubic Solved Again. Heuristic Programming in Artificial Intelligence 3: The Third Computer Olympiad
- Martin Schijf (1993). Proof-number Search and Transpositions. M.Sc. thesis, Leiden University
- Victor Allis (1994). Searching for Solutions in Games and Artificial Intelligence. Ph.D. thesis, University of Limburg, pdf
- Dennis Breuker, Victor Allis, Jaap van den Herik (1994). How to Mate: Applying Proof-Number Search. Advances in Computer Chess 7, reprint as Mate in 38: Applying Proof-Number Search from Ed Schroder's Programmer's Stuff site
- Victor Allis, Maarten van der Meulen, Jaap van den Herik (1994). Proof-Number Search. Artificial Intelligence, Vol. 66, No. 1
- Martin Schijf, Victor Allis, Jos Uiterwijk (1994). Proof-Number Search and Transpositions. ICCA Journal, Vol. 17, No. 2
1995 ...
- Masahiro Seo (1995). The C* Algorithm for AND/OR Tree Search and Its Application to a Tsume-Shogi Program. M.Sc. thesis, University of Tokyo, ps
- Dennis Breuker (1998). Memory versus Search in Games. Ph.D. thesis, Maastricht University, Chapter 3: The proof-number search algorithm, Chapter 4: The pn2-search algorithm
- Ayumu Nagai (1998). A new AND/OR Tree Search Algorithm Using Proof Number and Disproof Number. Complex Games Lab Workshop, Tsukuba
- Ayumu Nagai (1999). A New Depth-First-Search Algorithm for AND/OR Trees. M.Sc. thesis, University of Tokyo
- Ayumu Nagai, Hiroshi Imai (1999). Proof for the Equivalence Between Some Best-First Algorithms and Depth-First Algorithms for AND/OR Trees. Proceedings of the Korea-Japan Joint Workshop on Algorithms and Computation
- Akihiro Kishimoto, Yoshiyuki Kotani (1999). Parallel AND/OR tree search based on proof and disproof numbers. 5th Game Programming Workshop
- Ayumu Nagai, Hiroshi Imai (1999). Application of df-pn+ to Othello endgames. 5th Game Programming Workshop » Othello
2000 ...
- Tristan Cazenave (2000). Abstract Proof Search. CG 2000, pdf
- Masahiro Seo, Hiroyuki Iida, Jos Uiterwijk (2001). The PN*-Search Algorithm: Applications to Tsume-Shogi. Artificial Intelligence, Vol. 129, Nos. 1-2
- Makoto Sakuta, Hiroyuki Iida (2001). The Performance of PN*, PDS, and PN Search on 6x6 Othello and Tsume-Shogi. Advances in Computer Games 9
- Dennis Breuker, Jos Uiterwijk, Jaap van den Herik (2001). The PN2-Search Algorithm. Advances in Computer Games 9
- Mark Winands, Jos Uiterwijk (2001). PN, PN2 and PN* in Lines of Action. 6th Computer Olympiad Workshop, pdf » Lines of Action
- Makoto Sakuta, Hiroyuki Iida (2001). AND/OR-tree Search Algorithms in Shogi Mating Search. ICGA Journal, Vol. 24, No. 4
- Martin Müller (2001). Proof-Set Search. Technical Report TR 01-09, University of Alberta CiteSeerX [26]
- Martin Müller (2002). Proof-Set Search. CG 2002
- Mark Winands, Jos Uiterwijk, Jaap van den Herik (2002). PDS-PN: A New Proof-Number Search Algorithm: Application to Lines of Action. CG 2002 » Lines of Action
- Ayumu Nagai (2002). Df-pn Algorithm for Searching AND/OR Trees and Its Applications. Ph.D. thesis, University of Tokyo
- Ayumu Nagai, Hiroshi Imai (2002). Proof for the Equivalence Between Some Best-First Algorithms and Depth-First Algorithms for AND/OR Trees. IEICE transactions on information and systems
- Akihiro Kishimoto, Martin Müller (2003). Df-pn in Go: An Application to the One-Eye Problem. Advances in Computer Games 10, pdf » Go [27]
- Mark Winands, Jos Uiterwijk, Jaap van den Herik (2004). An Effective Two-Level Proof-Number Search Algorithm. Theoretical Computer Science. Vol. 313, No.3, pp. 511-525. ps
- Mark Winands (2004). Informed Search in Complex Games. Ph.D. thesis, Universiteit Maastricht, Received the 2004 ChessBase Best-Publication Award, pdf, Chapter 4 - Proof-Number Search Algorithm, Chapter 5 - An Effective Two-Level Proof-Number Search Algorithm
2005 ...
- Akihiro Kishimoto (2005). Correct and Efficient Search Algorithms in the Presence of Repetitions. Ph.D. thesis, University of Alberta, Received the 2005 ChessBase Best-Publication Award, pdf
- Akihiro Kishimoto, Martin Müller (2005). A Solution to the GHI Problem for Depth-First Proof-Number Search. 7th Joint Conference on Information Sciences (JCIS2003), pp. 489 - 492, pdf » Graph History Interaction
- Jonathan Schaeffer, Yngvi Björnsson, Neil Burch, Akihiro Kishimoto, Martin Müller, Rob Lake, Paul Lu, Steve Sutphen (2005). Solving Checkers. IJCAI 2005, pdf
- Jaap van den Herik, Jeroen Donkers, Jos Uiterwijk, Guillaume Chaslot, Sander Bakkes, Jahn-Takeshi Saito (2006). Intelligent Search Techniques Proof-Number Search. MICC/IKAT Universiteit Maastricht
- Jahn-Takeshi Saito, Guillaume Chaslot, Jos Uiterwijk, Jaap van den Herik (2006). Monte-Carlo Proof-Number Search for Computer Go. CG 2006
- Jakub Pawlewicz, Łukasz Lew (2006). Improving Depth-first PN-Search: 1 + ε Trick. CG 2006, pdf
- Kazuki Yoshizoe, Akihiro Kishimoto, Martin Müller. (2007). Lambda Depth-First Proof-Number Search and Its Application to Go. IJCAI 2007, pdf
- Kazuki Yoshizoe (2008). A New Proof-Number Calculation Technique for Proof-Number Search. CG 2008
- Akihiro Kishimoto, Martin Müller (2008). About the Completeness of Depth-First Proof-Number Search. CG 2008
- Toru Ueda, Tsuyoshi Hashimoto, Junichi Hashimoto, Hiroyuki Iida (2008). Weak Proof-Number Search. CG 2008
- Kazuki Yoshizoe (2009). AND-OR Tree Search Algorithms for Domains with Uniform Branching Factors. Ph.D. thesis, University of Tokyo
- Jahn-Takeshi Saito, Mark Winands, Jaap van den Herik (2009). Randomized Parallel Proof-Number Search. Advances in Computer Games 12, pdf
- Changming Xu, Zongmin Ma, Junjie Tao, Xinhe Xu (2009). Enhancements of Proof Number Search in Connect6. IEEE Control and Decision Conference
2010 ...
- Ping-Hung Lin (2010). Relevance-Zone-Oriented Proof Search for Connect6. Ph.D. thesis
- Mark Winands, Maarten Schadd (2010). Evaluation-Function Based Proof-Number Search. CG 2010, pdf
- I-Chen Wu, Hung-Hsuan Lin, Ping-Hung Lin, Der-Johng Sun, Yi-Chih Chan, Bo-Ting Chen (2010). Job-Level Proof-Number Search for Connect6. CG 2010
- I-Chen Wu, Ping-Hung Lin (2010). Relevance-Zone-Oriented Proof Search for Connect6. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 2, No. 3 » Connect6
- Shi-Jim Yen, Jung-Kuei Yang (2010). Searching for Stage Proof Number in Connect6. TAAI 2010
- Tomoyuki Kaneko (2010). Parallel Depth First Proof Number Search. AAAI 2010
- Abdallah Saffidine, Nicolas Jouandeau, Tristan Cazenave (2011). Solving Breakthrough with Race Patterns and Job-Level Proof Number Search. Advances in Computer Games 13 » Breakthrough (Game)
- Akihiro Kishimoto, Mark Winands, Martin Müller, Jahn-Takeshi Saito (2012). Game-Tree Search using Proof Numbers: The First Twenty Years. ICGA Journal, Vol. 35, No. 3
- Abdallah Saffidine (2012). Minimal Proof Search for Modal Logic K Model Checking. CoRR, July 2012 [28]
- Abdallah Saffidine, Tristan Cazenave (2012). Multiple-Outcome Proof Number Search. ECAI 2012
- Kunihito Hoki, Tomoyuki Kaneko, Akihiro Kishimoto, Takeshi Ito (2013). Parallel Dovetailing and its Application to Depth-First Proof-Number Search. ICGA Journal, Vol. 36, No. 1 [29]
- Abdallah Saffidine (2013). Solving Games and All That. Ph.D. thesis, 2.4 Proof Number Search
- I-Chen Wu, Hung-Hsuan Lin, Der-Johng Sun, Kuo-Yuan Kao, Ping-Hung Lin, Yi-Chih Chan, Bo-Ting Chen (2013). Job-Level Proof Number Search. IEEE Transactions on Computational Intelligence and AI in Games, Vol. 5, No. 1
- Jakub Pawlewicz, Ryan Hayward (2013). Scalable Parallel DFPN Search. CG 2013, pdf
- Mark Watkins (2014). Solved Openings in Losing Chess. ICGA Journal, Vol. 37, No. 2 » Losing Chess
2015 ...
- Taichi Ishitobi, Aske Plaat, Hiroyuki Iida, Jaap van den Herik (2015). Reducing the Seesaw Effect with Deep Proof Number Search. Advances in Computer Games 14
- Jiaxing Song (2017). Deep df-pn and its Efficient Implementations. Advances in Computer Games 15
- Chao Gao, Martin Müller, Ryan Hayward (2017). Focused Depth-first Proof Number Search using Convolutional Neural Networks for the Game of Hex. IJCAI 2017
Forum Posts
- Re: One mate to solve...(proof number search results) by Angrim, CCC, May 16, 2001
- Re: A new(?) technique to recognize draws by Dan Andersson, CCC, June 01, 2002
- Proof number & conspiracy search by Eli Liang, CCC, August 29, 2002
- Mixing alpha-beta with PN search by Tord Romstad, CCC, January 18, 2004 » Alpha-Beta
- Upper bound on proof tree size by Forrest Hoch, CCC, July 11, 2014
- Proof-number search by Harm Geert Muller, CCC, October 20, 2016 » Crazyhouse
External Links
Proof
- Mathematical induction from Wikipedia
- Proof by exhaustion from Wikipedia
- Proof theory from Wikipedia
- Proof calculus from Wikipedia
- Method of analytic tableaux from Wikipedia
Misc
- Marcus Miller & Herbie Hancock's Headhunters'05 - Actual Proof, Live at Tokyo Jazz 2005, YouTube Video
- Herbie Hancock: The Imagine Project - Actual Proof, Montreux Jazz Festival, July 16, 2010, YouTube Video
References
- ↑ Paul Klee - Tree Nursery, The Phillips Collection, Wikimedia Commons
- ↑ Victor Allis (1994). Searching for Solutions in Games and Artificial Intelligence. Ph.D. thesis, University of Limburg, pdf
- ↑ Victor Allis, Maarten van der Meulen, Jaap van den Herik (1994). Proof-Number Search. Artificial Intelligence, Vol. 66, No. 1
- ↑ Akihiro Kishimoto, Mark Winands, Martin Müller, Jahn-Takeshi Saito (2012). Game-Tree Search using Proof Numbers: The First Twenty Years. ICGA Journal, Vol. 35, No. 3
- ↑ Jaap van den Herik (2012). All is Proof Numbers. ICGA Journal, Vol. 35, No. 3 (editorial)
- ↑ Akihiro Kishimoto, Mark Winands, Martin Müller, Jahn-Takeshi Saito (2012). Game-Tree Search using Proof Numbers: The First Twenty Years. ICGA Journal, Vol. 35, No. 3
- ↑ Victor Allis (1994). Searching for Solutions in Games and Artificial Intelligence. Ph.D. thesis, University of Limburg
- ↑ Akihiro Kishimoto, Mark Winands, Martin Müller, Jahn-Takeshi Saito (2012). Game-Tree Search using Proof Numbers: The First Twenty Years. ICGA Journal, Vol. 35, No. 3
- ↑ Martin Schijf (1993). Proof-number Search and Transpositions. M.Sc. thesis, Leiden University
- ↑ Dennis Breuker (1998). Memory versus Search in Games. Ph.D. thesis, Maastricht University, Chapter 4: The pn2-search algorithm
- ↑ Masahiro Seo (1995). The C* Algorithm for AND/OR Tree Search and Its Application to a Tsume-Shogi Program. M.Sc. thesis, University of Tokyo, ps
- ↑ Masahiro Seo, Hiroyuki Iida, Jos Uiterwijk (2001). The PN*-Search Algorithm: Applications to Tsume-Shogi. Artificial Intelligence, Vol. 129, Nos. 1-2
- ↑ Richard Korf (1993). Linear-Space Best-First Search. Artificial Intelligence, Vol. 62, No. 1, pdf
- ↑ Ayumu Nagai (2002). Df-pn Algorithm for Searching AND/OR Trees and Its Applications. Ph.D. thesis, University of Tokyo
- ↑ Mark Winands, Jos Uiterwijk, Jaap van den Herik (2002). PDS-PN: A new proofnumber search algorithm: Application to Lines of Action. CG 2002, pdf
- ↑ Akihiro Kishimoto, Yoshiyuki Kotani (1999). Parallel AND/OR tree search based on proof and disproof numbers. 5th Game Programming Workshop
- ↑ Tomoyuki Kaneko (2010). Parallel Depth First Proof Number Search. AAAI 2010
- ↑ Akihiro Kishimoto, Mark Winands, Martin Müller, Jahn-Takeshi Saito (2012). Game-Tree Search using Proof Numbers: The First Twenty Years. ICGA Journal, Vol. 35, No. 3
- ↑ Victor Allis (1988). A Knowledge-Based Approach of Connect Four: The Game is Over, White to Move Wins. M.Sc. thesis, Report No. IR-163, Faculty of Mathematics and Computer Science, Vrije Universteit, Amsterdam
- ↑ Charles Elkan (1989). Conspiracy Numbers and Caching for Searching And/Or Trees and Theorem-Proving. IJCAI 1989, pdf
- ↑ Akihiro Kishimoto, Martin Müller (2003). Df-pn in Go: An Application to the One-Eye Problem. Advances in Computer Games 10, pdf
- ↑ Jonathan Schaeffer, Neil Burch, Yngvi Björnsson, Akihiro Kishimoto, Martin Müller, Rob Lake, Paul Lu, Steve Sutphen (2007). Checkers is Solved. Science, Vol. 317, no. 5844
- ↑ Jonathan Schaeffer, Yngvi Björnsson, Neil Burch, Akihiro Kishimoto, Martin Müller, Rob Lake, Paul Lu, Steve Sutphen (2005). Solving Checkers. IJCAI 2005
- ↑ Dennis Breuker, Victor Allis, Jaap van den Herik (1994). How to Mate: Applying Proof-Number Search. Advances in Computer Chess 7, reprint as Mate in 38: Applying Proof-Number Search from Ed Schroder's Programmer's Stuff site
- ↑ Sjeng : Download / proof.c
- ↑ Re: A new(?) technique to recognize draws by Dan Andersson, CCC, June 01, 2002
- ↑ Tsumego at Sensei's Library
- ↑ Modal logic from Wikipedia
- ↑ Dovetailing (computer science) from Wikipedia