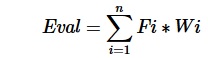Evaluation
Home * Evaluation
Evaluation,
a heuristic function to determine the relative value of a position, i.e. the chances of winning. If we could see to the end of the game in every line, the evaluation would only have values of -1 (loss), 0 (draw), and 1 (win), and the chess engine should search to depth 1 only to get the best move. In practice, however, we do not know the exact value of a position, so we must make an approximation with the main purpose is to compare positions, and the chess engine now must search deeply and find the highest score position within a given period.
Recently, there are two main ways to build an evaluation: traditional hand-crafted evaluation (HCE) and multi-layer neural networks. This page focuses on the traditional way considering explicit features of a chess position.
Beginning chess players learn to do this starting with the value of the pieces themselves. Computer evaluation functions also use the value of the material balance as the most significant aspect and then add other considerations.
Contents
Where to Start
The first thing to consider when writing an evaluation function is how to score a move in Minimax or the more common NegaMax framework. While Minimax usually associates the white side with the max-player and black with the min-player and always evaluates from the white point of view, NegaMax requires a symmetric evaluation in relation to the side to move. We can see that one must not score the move per se – but the result of the move (i.e. a positional evaluation of the board as a result of the move). Such a symmetric evaluation function was first formulated by Claude Shannon in 1949 [2] :
f(p) = 200(K-K')
+ 9(Q-Q')
+ 5(R-R')
+ 3(B-B' + N-N')
+ 1(P-P')
- 0.5(D-D' + S-S' + I-I')
+ 0.1(M-M') + ...
KQRBNP = number of kings, queens, rooks, bishops, knights and pawns
D,S,I = doubled, blocked and isolated pawns
M = Mobility (the number of legal moves)
Here, we can see that the score is returned as a result of subtracting the current side's score from the equivalent evaluation of the opponent's board scores (indicated by the prime letters K' Q' and R'.. ).
Side to move relative
In order for NegaMax to work, it is important to return the score relative to the side being evaluated. For example, consider a simple evaluation, which considers only material and mobility:
materialScore = kingWt * (wK-bK)
+ queenWt * (wQ-bQ)
+ rookWt * (wR-bR)
+ knightWt* (wN-bN)
+ bishopWt* (wB-bB)
+ pawnWt * (wP-bP)
mobilityScore = mobilityWt * (wMobility-bMobility)
return the score relative to the side to move (who2Move = +1 for white, -1 for black):
Eval = (materialScore + mobilityScore) * who2Move
Linear vs. Nonlinear
Most evaluations terms are a linear combination of independent features and associated weights in the form of
A function f is linear if the function is additive:
and second if the function is homogeneous of degree 1:
It depends on the definition and independence of features and the acceptance of the axiom of choice (Ernst Zermelo 1904), whether additive real number functions are linear or not [3] . Features are either related to single pieces (material), their location (piece-square tables), or more sophisticated, considering interactions of multiple pawns and pieces, based on certain patterns or chunks. Often several phases to first process simple features and after building appropriate data structures, in consecutive phases more complex features based on patterns and chunks are used.
Based on that, to distinguish first-order, second-order, etc. terms, makes more sense than using the arbitrary terms linear vs. nonlinear evaluation [4] . With respect to tuning, one has to take care that features are independent, which is not always that simple. Hidden dependencies may otherwise make the evaluation function hard to maintain with undesirable nonlinear effects.
General Aspects
Basic Evaluation Features
- Material
- Piece-Square Tables
- Pawn Structure
- Evaluation of Pieces
- Evaluation Patterns
- Mobility
- Center Control
- Connectivity
- Trapped Pieces
- King Safety
- Space
- Tempo
Considering Game Phase
- Evaluation Discontinuity
- Tapered Eval (a score is interpolated between opening and endgame based on game stage/pieces)
Miscellaneous
- Analog Evaluation
- Asymmetric Evaluation
- Automated Tuning
- Evaluation Function
- Evaluation Function Draft
- Evaluation Hash Table
- Evaluation Overlap by Mark Watkins
- Evaluation Patterns
- Lazy Evaluation
- Quantifying Evaluation Features by Mark Watkins
- Simplified Evaluation Function
- PeSTO's Evaluation Function
See also
- CPW-Engine_eval - an example of a medium strength evaluation function
- Entropy in Papa
- Evaluation in Kaissa (PC)
- Evaluation in Rookie 2.0
- Knowledge
Publications
1949
- Claude Shannon (1949). Programming a Computer for Playing Chess. pdf from The Computer History Museum
1950 ...
- Eliot Slater (1950). Statistics for the Chess Computer and the Factor of Mobility, Proceedings of the Symposium on Information Theory, London. Reprinted 1988 in Computer Chess Compendium, pp. 113-117. Including the transcript of a discussion with Alan Turing and Jack Good
- Alan Turing (1953). Chess. part of the collection Digital Computers Applied to Games, in Bertram Vivian Bowden (editor), Faster Than Thought, a symposium on digital computing machines, reprinted 1988 in Computer Chess Compendium, reprinted 2004 in The Essential Turing, google books
1960 ...
- Israel Albert Horowitz, Geoffrey Mott-Smith (1960,1970,2012). Point Count Chess. Samuel Reshevsky (Introduction), Sam Sloan (2012 Introduction), Amazon [5]
- Jack Good (1968). A Five-Year Plan for Automatic Chess. Machine Intelligence II pp. 110-115
1970 ...
- Ron Atkin (1972). Multi-Dimensional Structure in the Game of Chess. In International Journal of Man-Machine Studies, Vol. 4
- Ron Atkin, Ian H. Witten (1975). A Multi-Dimensional Approach to Positional Chess. International Journal of Man-Machine Studies, Vol. 7, No. 6
- Gerard Zieliński (1976). Simple Evaluation Function. Kybernetes, Vol. 5, No. 3
- Ron Atkin (1977). Positional Play in Chess by Computer. Advances in Computer Chess 1
- David Slate, Larry Atkin (1977). CHESS 4.5 - The Northwestern University Chess Program. Chess Skill in Man and Machine (ed. Peter W. Frey), pp. 82-118. Springer-Verlag, New York, N.Y. 2nd ed. 1983. ISBN 0-387-90815-3. Reprinted (1988) in Computer Chess Compendium
- Hans Berliner (1979). On the Construction of Evaluation Functions for Large Domains. IJCAI 1979 Tokyo, Vol. 1, pp. 53-55.
1980 ...
- Helmut Horacek (1984). Some Conceptual Defects of Evaluation Functions. ECAI-84, Pisa, Elsevier
- Peter W. Frey (1985). An Empirical Technique for Developing Evaluation Functions. ICCA Journal, Vol. 8, No. 1
- Tony Marsland (1985). Evaluation-Function Factors. ICCA Journal, Vol. 8, No. 2, pdf
- Jens Christensen, Richard Korf (1986). A Unified Theory of Heuristic Evaluation functions and Its Applications to Learning. Proceedings of the AAAI-86, pp. 148-152, pdf
- Dap Hartmann (1987). How to Extract Relevant Knowledge from Grandmaster Games. Part 1: Grandmasters have Insights - the Problem is what to Incorporate into Practical Problems. ICCA Journal, Vol. 10, No. 1
- Dap Hartmann (1987). How to Extract Relevant Knowledge from Grandmaster Games. Part 2: the Notion of Mobility, and the Work of De Groot and Slater. ICCA Journal, Vol. 10, No. 2
- Bruce Abramson, Richard Korf (1987). A Model of Two-Player Evaluation Functions. AAAI-87. pdf
- Kai-Fu Lee, Sanjoy Mahajan (1988). A Pattern Classification Approach to Evaluation Function Learning. Artificial Intelligence, Vol. 36, No. 1
- Dap Hartmann (1989). Notions of Evaluation Functions Tested against Grandmaster Games. Advances in Computer Chess 5
- Maarten van der Meulen (1989). Weight Assessment in Evaluation Functions. Advances in Computer Chess 5
- Bruce Abramson (1989). On Learning and Testing Evaluation Functions. Proceedings of the Sixth Israeli Conference on Artificial Intelligence, 1989, 7-16.
- Danny Kopec, Ed Northam, David Podber, Yehya Fouda (1989). The Role of Connectivity in Chess. Workshop on New Directions in Game-Tree Search, pdf
1990 ...
- Bruce Abramson (1990). On Learning and Testing Evaluation Functions. Journal of Experimental and Theoretical Artificial Intelligence 2: 241-251.
- Ron Kalnim (1990). A Positional Assembly Model. ICCA Journal, Vol. 13, No. 3
- Paul E. Utgoff, Jeffery A. Clouse (1991). Two Kinds of Training Information for Evaluation Function Learning. University of Massachusetts, Amherst, Proceedings of the AAAI 1991
- Ingo Althöfer (1991). An Additive Evaluation Function in Chess. ICCA Journal, Vol. 14, No. 3
- Ingo Althöfer (1993). On Telescoping Linear Evaluation Functions. ICCA Journal, Vol. 16, No. 2 [6]
- Alois Heinz, Christoph Hense (1993). Bootstrap learning of α-β-evaluation functions. ICCI 1993, pdf
- Alois Heinz (1994). Efficient Neural Net α-β-Evaluators. pdf [7]
- Peter Mysliwietz (1994). Konstruktion und Optimierung von Bewertungsfunktionen beim Schach. Ph.D. Thesis (German)
- Don Beal, Martin C. Smith (1994). Random Evaluations in Chess. ICCA Journal, Vol. 17, No. 1
- Yaakov HaCohen-Kerner (1994). Case-Based Evaluation in Computer Chess. EWCBR 1994
- Michael Buro (1995). Statistical Feature Combination for the Evaluation of Game Positions. JAIR, Vol. 3
- Peter Mysliwietz (1997). A Metric for Evaluation Functions. Advances in Computer Chess 8
- Michael Buro (1998). From Simple Features to Sophisticated Evaluation Functions. CG 1998, pdf
2000 ...
- Dan Heisman (2003). Evaluation Criteria, pdf from ChessCafe.com
- Jeff Rollason (2005). Evaluation by Hill-climbing: Getting the right move by solving micro-problems. AI Factory, Autumn 2005 » Automated Tuning
- Shogo Takeuchi, Tomoyuki Kaneko, Kazunori Yamaguchi, Satoru Kawai (2007). Visualization and Adjustment of Evaluation Functions Based on Evaluation Values and Win Probability. AAAI 2007
- Omid David, Moshe Koppel, Nathan S. Netanyahu (2008). Genetic Algorithms for Mentor-Assisted Evaluation Function Optimization, ACM Genetic and Evolutionary Computation Conference (GECCO '08), pp. 1469-1475, Atlanta, GA, July 2008.
- Omid David, Jaap van den Herik, Moshe Koppel, Nathan S. Netanyahu (2009). Simulating Human Grandmasters: Evolution and Coevolution of Evaluation Functions. ACM Genetic and Evolutionary Computation Conference (GECCO '09), pp. 1483 - 1489, Montreal, Canada, July 2009.
- Omid David (2009). Genetic Algorithms Based Learning for Evolving Intelligent Organisms. Ph.D. Thesis.
2010 ...
- Lyudmil Tsvetkov (2010). Little Chess Evaluation Compendium. 2010 pdf
- Omid David, Moshe Koppel, Nathan S. Netanyahu (2011). Expert-Driven Genetic Algorithms for Simulating Evaluation Functions. Genetic Programming and Evolvable Machines, Vol. 12, No. 1, pp. 5--22, March 2011. » Genetic Programming
- Jeff Rollason (2011). Mixing MCTS with Conventional Static Evaluation. AI Factory, Winter 2011 » Monte-Carlo Tree Search
- Jeff Rollason (2012). Evaluation options - Overview of methods. AI Factory, Summer 2012
- Lyudmil Tsvetkov (2012). An Addendum to a Little Chess Evaluation Compendium. Addendum June 2012 pdf, File:Addendum2LCEC 2012.pdf, File:Addendum3LCEC 2012.pdf, Addendum 4 November 2012 pdf, File:Addendum5LCEC 2012.pdf, File:Addendum6LCEC 2012.pdf
- Lyudmil Tsvetkov (2012). Little Chess Evaluation Compendium. July 2012 pdf [8], File:LittleChessEvaluationCompendium.pdf
- Derek Farren, Daniel Templeton, Meiji Wang (2013). Analysis of Networks in Chess. Team 23, Stanford University, pdf
2015 ...
- Nera Nesic, Stephan Schiffel (2016). Heuristic Function Evaluation Framework. CG 2016
- Lyudmil Tsvetkov (2017). The Secret of Chess. amazon [9]
- Lyudmil Tsvetkov (2017). Pawns. amazon
Blog & Forum Posts
1993 ...
- Cray Blitz Evaluation by Robert Hyatt, rgc, March 05, 1993 » Cray Blitz
- Mobility Measure: Proposed Algorithm by Dietrich Kappe, rgc, September 23, 1993 » Mobility
- bitboard position evaluations by Robert Hyatt, rgc, November 17, 1994 » Bitboards
1995 ...
- Value of the pieces by Joost de Heer, rgc, February 01, 1995
- Evaluation function diminishing returns by Bruce Moreland, rgcc, February 1, 1997
- Evaluation function question by Dave Fotland, rgcc, February 07, 1997
- computer chess "oracle" ideas... by Robert Hyatt, rgcc, April 01, 1997 » Oracle
- Evolutionary Evaluation by Daniel Homan, rgcc, September 09, 1997 » Automated Tuning
- Books that help for evaluation by Guido Schimmels, CCC, August 18, 1998
- Static evaluation after the "Positional/Real Sacrifice" by Andrew Williams, CCC, December 03, 1999
2000 ...
- Adding knowledge to the evaluation, what am I doing wrong? by Albert Bertilsson, CCC, March 13, 2003
- testing of evaluation function by Steven Chu, CCC, April 17, 2003 » Engine Testing
- Question about evaluation and branch factor by Marcus Prewarski, CCC, November 20, 2003 » Branching Factor
- STATIC EVAL TEST (provisional) by Jaime Benito de Valle Ruiz, CCC, February 21, 2004 » Test-Positions
2005 ...
- Re: Zappa Report by Ingo Althöfer, CCC, December 30, 2005
- Do you evaluate internal nodes? by Tord Romstad, Winboard Forum, January 16, 2006 » Interior Node
- question about symmertic evaluation by Uri Blass, CCC, May 23, 2007
- Trouble Spotter by Harm Geert Muller, CCC, July 19, 2007 » Tactics
- Search or Evaluation? by Ed Schröder, Hiarcs Forum, October 05, 2007 » Search versus Evaluation, Search
- Re: Search or Evaluation? by Mark Uniacke, Hiarcs Forum, October 14, 2007
- Problems with eval function by Fermin Serrano, CCC, March 25, 2008 » Evaluation
- Evaluation functions. Why integer? by oysteijo, CCC, August 06, 2008 » Float, Score
- Smooth evaluation by Fermin Serrano, CCC, September 29, 2008
- Evaluating every node? by Gregory Strong, CCC, January 03, 2009
- Evaluation idea by Fermin Serrano, CCC, February 24, 2009
- Accurate eval function by Fermin Serrano, CCC, March 18, 2009
- Eval Dilemma by Edsel Apostol, CCC, April 03, 2009
- Linear vs. Nonlinear Evalulation by Gerd Isenberg, CCC, August 26, 2009
- Threat information from evaluation to inform q-search by Gary, CCC, September 15, 2009 » Quiescence Search
2010 ...
- Correcting Evaluation with the hash table by Mark Lefler, CCC, February 05, 2010
- Re: Questions for the Stockfish team by Milos Stanisavljevic, CCC, July 20, 2010
- Most important eval elements by Tom King, CCC, September 17, 2010
- Re: 100 long games Rybka 4 vs Houdini 1.03a by Tord Romstad, CCC, November 02, 2010
- dynamically modified evaluation function by Don Dailey, CCC, December 20, 2010
2011
- Suppose Rybka used Fruits evaluations by SR, Rybka Forum, August 29, 2011
- writing an evaluation function by Pierre Bokma, CCC, December 27, 2011
2012
- The evaluation value and value returned by minimax search by Chao Ma, CCC, March 09, 2012
- Multi dimensional score by Nicu Ionita, CCC, April 20, 2012
- Bi dimensional static evaluation by Nicu Ionita, CCC, April 20, 2012
- Theorem proving positional evaluation by Nicu Ionita, CCC, April 20, 2012
- log(w/b) instead of w-b? by Gerd Isenberg, CCC, May 02, 2012
- The value of an evaluation function by Ed Schröder, CCC, June 11, 2012
2013
- eval scale in Houdini by Rein Halbersma, CCC, January 14, 2013 » Houdini
- An idea of how to make your engine play more rational chess by Pio Korinth, CCC, January 25, 2013
- A Materialless Evaluation? by Thomas Kolarik, CCC, June 12, 2013
- A different way of summing evaluation features by Pio Korinth, CCC, July 14, 2013 [10] [11]
- Improve the search or the evaluation? by Jens Bæk Nielsen, CCC, August 31, 2013 » Search versus Evaluation
- Multiple EVAL by Ed Schroder, CCC, September 22, 2013
- floating point SSE eval by Marco Belli, CCC, December 13, 2013 » Float, Score
2014
- 5 underestimated evaluation rules by Lyudmil Tsvetkov, CCC, January 23, 2014
- Thoughs on eval terms by Fermin Serrano, CCC, March 31, 2014
2015 ...
- Value of a Feature or Heuristic by Jonathan Rosenthal, CCC, February 15, 2015
- Couple more ideas by Lyudmil Tsvetkov, CCC, April 05, 2015
- Most common/top evaluation features? by Alexandru Mosoi, CCC, April 10, 2015
- eval pieces by Daniel Anulliero, CCC, June 15, 2015
- * vs + by Stefano Gemma, CCC, July 19, 2015
- (E)valuation (F)or (S)tarters by Ed Schröder, CCC, July 26, 2015
2016
- Non-linear eval terms by J. Wesley Cleveland, CCC, January 29, 2016
- A bizarre evaluation by Larry Kaufman, CCC, March 20, 2016
- Chess position evaluation with convolutional neural network in Julia by Kamil Czarnogorski, Machine learning with Julia and python, April 02, 2016 » Deep Learning, Neural Networks
- Calculating space by Shawn Chidester, CCC, August 07, 2016
- Evaluation values help by Laurie Tunnicliffe, CCC, August 26, 2016
- A database for learning evaluation functions by Álvaro Begué, CCC, October 28, 2016 » Automated Tuning, Learning, Texel's Tuning Method
- Evaluation doubt by Fabio Gobbato, CCC, October 29, 2016
2017
- Bayesian Evaluation Functions by Jonathan Rosenthal, CCC, February 15, 2017
- improved evaluation function by Alexandru Mosoi, CCC, March 11, 2017 » Texel's Tuning Method, Zurichess
- random evaluation perturbation factor by Stuart Cracraft, CCC, April 24, 2017
- horrid positional play in a solid tactical searcher by Stuart Cracraft, CCC, April 29, 2017
- Another attempt at comparing Evals ELO-wise by Kai Laskos, CCC, May 22, 2017 » Playing Strength
- static eval in every node? by Erin Dame, CCC, June 09, 2017
- comparing between search or evaluation by Uri Blass, CCC, October 09, 2017» Search
- Neural networks for chess position evaluation- request by Kamil Czarnogorski, CCC, November 13, 2017 » Deep Learning, Neural Networks
- AlphaGo's evaluation function by Jens Kipper, CCC, November 26, 2017
- Logarithmic Patterns In Evaluations by Dennis Sceviour, CCC, December 09, 2017
2018
- replace the evaluation by playing against yourself by Uri Blass, CCC, January 25, 2018 » Fortress
- Poor man's neurones by Pawel Koziol, CCC, May 21, 2018 » Neural Networks
- Xiangqi evaluation by Harm Geert Muller, CCC, July 01, 2018 » Xiangqi
2020 ...
- romantic-style play by Stuart Cracraft, CCC, August 02, 2020
- Engine choosing between sets of piece/square tables by Pawel Koziol, ProDeo Forum, December 05, 2020 » Rodent, Piece-Square Tables
- Controlled randomness of evaluation function by nescitus, ProDeo Forum, December 06, 2020
- Manually tuned evaluation by Maksim Korzh, CCC, December 27, 2020 » Simplified Evaluation Function
2021
- So what do we miss in the traditional evaluation? by Ferdinand Mosca, CCC, January 29, 2021 » NNUE
- HCE and NNUE and vectorisation by Vivien Clauzon, CCC, February 11, 2021 » NNUE, Minic
- Idea: use range (evalMin - evalMax) for position evaluation by Mirza Hadzic, LCZero Forum, April 6, 2021
- Re: Idea: use range (evalMin - evalMax) for position evaluation by Álvaro Begué, LCZero Forum, May 28, 2021 [12]
- Re: Idea: use range (evalMin - evalMax) for position evaluation by Warren D. Smith, LCZero Forum, May 29, 2021
- I declare that HCE is dead... by Andrew Grant, CCC, June 29, 2021 » Ethereal, NNUE
- Evaluation questions by Ellie Moore, CCC, August 16, 2021
External Links
Mathematical Foundations
- Heuristic from Wikipedia
- Linear combination from Wikipedia
- Linear independence from Wikipedia
- Orthogonality from Wikipedia
- Principal component analysis from Wikipedia
Chess Evaluation
- Evaluation function from Wikipedia
- Stockfish Evaluation Guide » Stockfish Evaluation Guide
- GitHub - gekomad/chess-engine-eval-debugger: Chess engine web evaluator by Giuseppe Cannella
- Evaluation: Basics of Micro-Max by Harm Geert Muller
- Chess Programming Part VI: Evaluation Functions by François-Dominic Laramée, gamedev.net, October 2000
- About the Values of Chess Pieces by Ralph Betza
References
- ↑ Vassily Kandinsky - Schach-Theorie | Art I love | Pinterest
- ↑ Claude Shannon (1949). Programming a Computer for Playing Chess. pdf
- ↑ Re: Linear vs. Nonlinear Evaluation by Tord Romstad, CCC, August 27, 2009
- ↑ Re: Linear vs. Nonlinear Evaluation by Robert Hyatt, CCC, August 27, 2009
- ↑ Re: Books that help for evaluation by Robert Hyatt, CCC, August 18, 1998
- ↑ Re: Zappa Report by Ingo Althöfer, CCC, December 30, 2005
- ↑ Re: Evaluation by neural network ? by Jay Scott, CCC, November 10, 1997
- ↑ An Update of the Addendum to the LittleCompendium by Lyudmil Tsvetkov, CCC, July 02, 2012
- ↑ The Secret of Chess by Lyudmil Tsvetkov, CCC, August 01, 2017
- ↑ Euclidean distance from Wikipedia
- ↑ Principal component analysis from Wikipedia
- ↑ Eric B. Baum, Warren D. Smith (1999). Propagating Distributions Up Directed Acyclic Graphs. Neural Computation, Vol. 11, No. 1