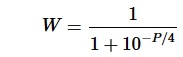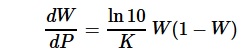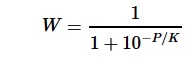Pawn Advantage, Win Percentage, and Elo
Home * Evaluation * Pawn Advantage, Win Percentage and Elo
An examination by Sune Fischer and Pradu Kannan in December 2007 on the approximate relations between Win Percentage, Pawn Advantage, and Elo rating advantage for computer chess resulted in following findings.
Contents
Relationship
It was found that the the approximate relationship between the winning probability W and the pawn advantage P is
The inverse relationship can be given as
From the above, the relationship between the equivalent Elo rating advantage R and the pawn advantage P can be given as
Data Acquisition
Data was taken from a collection of 405,460 computer games in PGN format. Whenever exactly 5 plys in a game had gone by without captures, the game result was accumulated twice in a table indexed by the material configuration. The data was accumulated twice because it was assumed that material values were equal for both colors. So if there was data for a KPK material configuration, the data was also tallied for the KKP. Only data pertaining to the material configuration was taken. This was considered reasonable because the material configuration is the most important quantity that affects the result of a game.
Data Reduction and Modeling
For each material configuration, a pawn value was computed using conventional pawn-normalized material ratios that are close to those used in strong chess programs (P=1, N=4, B=4.1, R=6, Q=12). The relationship between Win Percentage and Pawn Advantage was assumed to follow a logistic model [1] with its sigmoid curve, namely,
where K is an unknown non-zero constant. When applying the condition that the win probability is 0.5 if there is no pawn advantage, the solution to the above seperable differential equation becomes
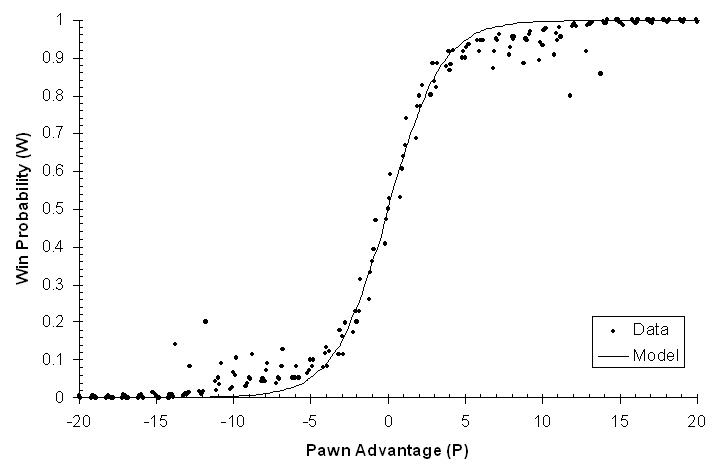
For K=4, the proposed logistic model and the data is plotted here for comparison:
See also
Publications
- Shogo Takeuchi, Tomoyuki Kaneko, Kazunori Yamaguchi, Satoru Kawai (2007). Visualization and Adjustment of Evaluation Functions Based on Evaluation Values and Win Probability. AAAI 2007, pdf
- Kenneth W. Regan, Tamal T. Biswas, Jason Zhou (2014). Human and Computer Preferences at Chess. pdf
- Tamal T. Biswas, Kenneth W. Regan (2015). Measuring Level-K Reasoning, Satisficing, and Human Error in Game-Play Data. IEEE ICMLA 2015, pdf preprint
- Shogo Takeuchi, Tomoyuki Kaneko (2015). Estimating Ratings of Computer Players by the Evaluation Scores and Principal Variations in Shogi. ACIT-CSI
Postings
1999
- Elo performance? by Stefan Meyer-Kahlen, CCC, May 22, 1999 » Match Statistics, Playing Strength
2000 ...
- likelihood instead of pawnunits? + chess knowledge by Ingo Lindam, CCC, October 25, 2002
- Winning percentage and centipawns by Luca Hemmerich, CCC, November 18, 2009
2010 ...
- Pawn Advantage, Win Percentage, and Elo by Adam Hair, CCC, April 15, 2012
- normal vs logistic curve for Elo model by Daniel Shawul, CCC, August 02, 2012
- Houdini, much weaker engines, and Arpad Elo by Kai Laskos, CCC, November 29, 2013 » Houdini, Match Statistics [2]
- Pawn Advantage in iCE by Thomas Petzke, mACE Chess, March 16, 2014 » iCE
- Using the Stockfish position evaluation score to predict victory probability by unavoidablegrain, Tumblr, September 28, 2014 » Stockfish
2015 ...
- Depth of Satisficing by Ken Regan, Gödel's Lost Letter and P=NP, October 06, 2015 » Depth, Match Statistics, Pawn Advantage, Win Percentage, and Elo, Stockfish, Komodo [3]
- Magnus and the Turkey Grinder by Ken Regan, Gödel's Lost Letter and P=NP, December 08, 2016 » Match Statistics [4] [5] [6]
- Statistical interpretation of search and eval scores by J. Wesley Cleveland, CCC, November 18, 2017 » Match Statistics, Score
- Why Lc0 eval (in cp) is asymmetric against AB engines? by Kai Laskos, CCC, July 25, 2018 » Asymmetric Evaluation, Leela Chess Zero
- UCI Win/Draw/Loss reporting by Gian-Carlo Pascutto, CCC, October 22, 2019
2020 ...
- Win-Draw-Loss evaluation by crem, LCZero blog, April 20, 2020 » TCEC Season 17 Superfinal
- Stockfish has included WDL stats in engine output by Deberger, CCC, July 02, 2020 » Stockfish
External Links
References
- ↑ logistic model from Wolfram MathWorld
- ↑ Arpad Elo - Wikipedia
- ↑ Regan's latest: Depth of Satisficing by Carl Lumma, CCC, October 09, 2015
- ↑ When Data Serves Turkey by Ken Regan, Gödel's Lost Letter and P=NP, November 30, 2016
- ↑ World Chess Championship 2016 from Wikipedia
- ↑ Regan's conundrum by Carl Lumma, CCC, December 09, 2016