Difference between revisions of "Match Statistics"

From Chessprogramming wiki
Jump to: navigation, search
Line 623: Line 623:
 
* [https://en.wikipedia.org/wiki/Probability_density_function Probability density function from Wikipedia]
 
* [https://en.wikipedia.org/wiki/Probability_density_function Probability density function from Wikipedia]
 
* [https://en.wikipedia.org/wiki/Likelihood_function Likelihood function from Wikipedia]
 
* [https://en.wikipedia.org/wiki/Likelihood_function Likelihood function from Wikipedia]
 +
* [https://en.wikipedia.org/wiki/Likelihood-ratio_test Likelihood-ratio test from Wikipedia]
 
* [https://en.wikipedia.org/wiki/P-value p-value from Wikipedia]
 
* [https://en.wikipedia.org/wiki/P-value p-value from Wikipedia]
 
* [https://en.wikipedia.org/wiki/Misunderstandings_of_p-values Misunderstandings of p-values from Wikipedia]
 
* [https://en.wikipedia.org/wiki/Misunderstandings_of_p-values Misunderstandings of p-values from Wikipedia]

Revision as of 00:17, 4 February 2020

Home * Engine Testing * Match Statistics

Match Statistics [1]

Match Statistics,
the statistics of chess tournaments and matches, that is a collection of chess games and the presentation, analysis, and interpretation of game related data, most common game results to determine the relative playing strength of chess playing entities, here with focus on chess engines. To apply match statistics, beside considering statistical population, it is conventional to hypothesize a statistical model describing a set of probability distributions.

Ratios / Operating Figures

Common tools, ratios and figures to illustrate a tournament outcome and provide a base for its interpretation.

Number of games

The total number of games played by an engine in a tournament. 

N = wins + draws + losses

Score

The score is a representation of the tournament-outcome from the viewpoint of a certain engine. 

score_difference = wins - losses

score = wins + draws/2

Win & Draw Ratio

win_ratio  = score/N

draw_ratio = draws/N

These two ratios depend on the strength difference between the competitors, the average strength level, the color and the drawishness of the opening book-line. Due to the second reason given, these ratios are very much influenced by the timecontrol, what is also confirmed by the published statistics of the testing orgnisations CCRL and CEGT, showing an increase of the draw rate at longer time controls. This correlation was also shown by Kirill Kryukov, who was analyzing statistics of his test-games [2] . The program playing white seems to be more supported by the additional level of strength. So, although one would expect with increasing draw rates the win ratio to approach 50%, in fact it is remaining about equal.

Timecontrol Draw Ratio Win Ratio (white) Source
40/4 30.9% 55.0% CEGT
40/20 35.6% 54.6% CEGT
40/120 41.3% 55.4% CEGT
40/120 (4cpu) 45.2% 55.9% CEGT
Timecontrol Draw Ratio Win Ratio (white) Source
40/4 31.0% 54.1% CCRL
40/40 37.2% 54.6% CCRL

Doubling Time Control As posted in October 2016 [3] , Andreas Strangmüller conducted an experiment with Komodo 9.3, time control doubling matches under Cutechess-cli, playing 3000 games with 1500 opening positions each, without pondering, learning, and tablebases, Intel i5-750 @ 3.5 GHz, 1 Core, 128 MB Hash [4] , see also Kai Laskos' 2013 results with Houdini 3 [5] and Diminishing Returns:

Time Control 2
vs 1 		20+0.2
10+0.1 		40+0.4
20+0.2 		80+0.8
40+0.4 		160+1.6
80+0.8 		320+3.2
160+1.6 		640+6.4
320+3.2 		1280+12.8
640+6.4 		2560+25.6
1280+12.8
Elo 144 133 112 101 93 73 59 51
Win 44.97% 41.27% 36.67% 32.67% 30.47% 25.17% 21.77% 18.97%
Draw 49.20% 54.00% 57.93% 63.03% 65.33% 70.47% 73.17% 76.63%
Loss 5.83% 4.73% 5.40% 4.30% 4.20% 4.37% 5.07% 4.40%

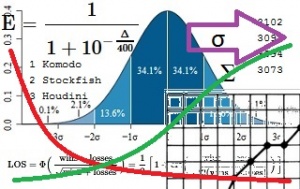
Elo-Rating & Win-Probability

see Pawn Advantage, Win Percentage, and Elo 

Expected win_ratio, win_probability (E)

Elo Rating Difference (Δ) = Elo_Player1 - Elo_Player2

E = 1 / ( 1 + 10-Δ/400)

Δ = 400 log10(E / (1 - E))

Generalization of the Elo-Formula: win_probability of player i in a tournament with n players 

Ei = 10Eloi / (10Elo1 + 10Elo2 + ... + 10Elon-1 + 10Elon)

Likelihood of Superiority

See LOS Table

The likelihood of superiority (LOS) denotes how likely it would be for two players of the same strength to reach a certain result - in other fields called a p-value, a measure of statistical significance of a departure from the null hypothesis [6]. Doing this analysis after the tournament one has to differentiate between the case where one knows that a certain engine is either stronger or equally strong (directional or one-tailed test) or the case where one has no information of whether the other engine is stronger or weaker (non-directional or two-tailed test). The latter due to the reduced information results in larger confidence intervals.

Two-tailed Test
Null- and alternative hypothesis: 

H0 : Elo_Player1 = Elo_Player2 

H1 : Elo_Player1 ≠ Elo_Player2 

LOS = P(Score > score of 2 programs with equal strength)

The probability of the null hypothesis being true can be calculated given the tournament outcome. In other words, how likely would it be for two players of the same strength to reach a certain result. The LOS would then be the inverse, 1 - the resulting probability.

For this type of analysis the trinomial distribution, a generalization of the binomial distribution, is needed. Whilest the binomial distribution can only calculate the probability to reach a certain outcome with two possible events, the trinominal distribution can account for all three possible events (win, draw, loss).

The following functions gives the probability of a certain game outcome assuming both players were of equal strength: 

win_probability = (1 - draw_ratio) / 2

P(wins,draws,losses) = N!/(wins! draws! losses!) win_probabilitywins draw_ratiodrwas win_probabilitylosses

This calculation becomes very inefficient for larger number of games. In this case the standard normal distribution can give a good approximation: 

N(N/2, N(1-draw_ratio))

where N(1 - draw_ratio) is the sum of wins and losses: 

N(N/2, wins + losses)

To calculate the LOS one needs the cumulative distribution function of the given normal distribution. However, as pointed out by Rémi Coulom, calculation can be done cleverly, and the normal approximation is not really required [7] . As further emphasized by Kai Laskos [8] and Rémi Coulom [9] [10] , draws do not count in LOS calculation and don't make a difference whether the game results were obtained when playing Black or White. It is a good approximation when the two players played the same number of games with each color: 

LOS = ϕ((wins - losses)/√(wins + losses))

LOS = ½[1 + erf((wins - losses)/√(2wins + 2losses))]

[11] [12] [13]

One-tailed Test
Null- and alternative hypothesis: 

H0 : Elo_Player1 ≤ Elo_Player2 

H1 : Elo_Player1 > Elo_Player2

Sample Program
A tiny C++11 program to compute Elo difference and LOS from W/L/D counts was given by Álvaro Begué [14] : 

#include <cstdio>
#include <cstdlib>
#include <cmath>

int main(int argc, char **argv) {
  if (argc != 4) {
    std::printf("Wrong number of arguments.\n\nUsage:%s <wins> <losses> <draws>\n", argv[0]);
    return 1;
  }
  int wins = std::atoi(argv[1]);
  int losses = std::atoi(argv[2]);
  int draws = std::atoi(argv[3]);

  double games = wins + losses + draws;
  std::printf("Number of games: %g\n", games);
  double winning_fraction = (wins + 0.5*draws) / games;
  std::printf("Winning fraction: %g\n", winning_fraction);
  double elo_difference = -std::log(1.0/winning_fraction-1.0)*400.0/std::log(10.0);
  std::printf("Elo difference: %+g\n", elo_difference);
  double los = .5 + .5 * std::erf((wins-losses)/std::sqrt(2.0*(wins+losses)));
  std::printf("LOS: %g\n", los);
}

Statistical Analysis

The trinomial versus the 5-nomial model

As indicated above a match between two engines is usually modeled as a sequence of independent trials taken from a trinomial distribution with probabilities (win_ratio,draw_ratio,loss_ratio). This model is appropriate for a match with randomly selected opening positions and randomly assigned colors (to maintain fairness). However one may show that under reasonable elo models the trinomial model is not correct in case games are played in pairs with reversed colors (as is commonly the case) and unbalanced opening positions are used.

This was also empirically observed by Kai Laskos [15] . He noted that the statistical predictions of the trinomial model do not match reality very well in the case of paired games. In particular he observed that for some data sets the variance of the match score as predicted by the trinomial model greatly exceeds the variance as calculated by the jackknife estimator. The jackknife estimator is a non-parametric estimator, so it does not depend on any particular statistical model. It appears the mismatch may even occur for balanced opening positions, an effect which can only be explained by the existence of correlations between paired games - something not considered by any elo model.

Over estimating the variance of the match score implies that derived quantities such as the number of games required to establish the superiority of one engine over another with a given level of significance are also over estimated. To obtain agreement between statistical predictions and actual measurements one may adopt the more general 5-nomial model. In the 5-nomial model the outcome of paired games is assumed to follow a 5-nomial distribution with probabilities 

(p0, p1/2, p1, p3/2, p2)

These unknown probabilities may be estimated from the outcome frequencies of the paired games and then subsequently be used to compute an estimate for the variance of the match score. Summarizing: in the case of paired games the 5-nomial model handles the following effects correctly which the trinomial model does not:

  • Unbalanced openings
  • Correlations between paired games

For further discussion on the potential use of unbalanced opening positions in engine testing see the posting by Kai Laskos [16] .

SPRT

The sequential probability ratio test (SPRT) is a specific sequential hypothesis test - a statistical analysis where the sample size is not fixed in advance - developed by Abraham Wald [17] . While originally developed for use in quality control studies in the realm of manufacturing, SPRT has been formulated for use in the computerized testing of human examinees as a termination criterion [18]. As mentioned by Arthur Guez in this 2015 Ph.D. thesis Sample-based Search Methods for Bayes-Adaptive Planning [19], Alan Turing assisted by Jack Good used a similar sequential testing technique to help decipher enigma codes at Bletchley Park [20]. SPRT is applied in Stockfish testing to terminate self-testing series early if the result is likely outside a given elo-window [21] . In August 2016, Michel Van den Bergh posted following Python code in CCC to implement the SPRT a la Cutechess-cli or Fishtest: [22] [23] 

from __future__ import division

import math

def LL(x):
    return 1/(1+10**(-x/400))

def LLR(W,D,L,elo0,elo1):
    """
This function computes the log likelihood ratio of H0:elo_diff=elo0 versus
H1:elo_diff=elo1 under the logistic elo model

expected_score=1/(1+10**(-elo_diff/400)).

W/D/L are respectively the Win/Draw/Loss count. It is assumed that the outcomes of
the games follow a trinomial distribution with probabilities (w,d,l). Technically
this is not quite an SPRT but a so-called GSPRT as the full set of parameters (w,d,l)
cannot be derived from elo_diff, only w+(1/2)d. For a description and properties of
the GSPRT (which are very similar to those of the SPRT) see

http://stat.columbia.edu/~jcliu/paper/GSPRT_SQA3.pdf

This function uses the convenient approximation for log likelihood
ratios derived here:

http://hardy.uhasselt.be/Toga/GSPRT_approximation.pdf

The previous link also discusses how to adapt the code to the 5-nomial model
discussed above.
"""
# avoid division by zero
    if W==0 or D==0 or  L==0:
        return 0.0
    N=W+D+L
    w,d,l=W/N,D/N,L/N
    s=w+d/2
    m2=w+d/4
    var=m2-s**2
    var_s=var/N
    s0=LL(elo0)
    s1=LL(elo1)
    return (s1-s0)*(2*s-s0-s1)/var_s/2.0

def SPRT(W,D,L,elo0,elo1,alpha,beta):
    """
This function sequentially tests the hypothesis H0:elo_diff=elo0 versus
the hypothesis H1:elo_diff=elo1 for elo0<elo1. It should be called after
each game until it returns either 'H0' or 'H1' in which case the test stops
and the returned hypothesis is accepted.

alpha is the probability that H1 is accepted while H0 is true
(a false positive) and beta is the probability that H0 is accepted
while H1 is true (a false negative). W/D/L are the current win/draw/loss
counts, as before.
"""
    LLR_=LLR(W,D,L,elo0,elo1)
    LA=math.log(beta/(1-alpha))
    LB=math.log((1-beta)/alpha)
    if LLR_>LB:
        return 'H1'
    elif LLR_<LA:
        return 'H0'
    else:
        return ''

Beside the above SPRT implementation using pentanomial frequencies and a simulation tool in Python [24] [25], Michel Van den Bergh wrote a much faster multi-threaded C version [26] [27].

Tournaments

See also

Publications

1920 ...

1940 ...

1950 ...

1960 ...

1970 ...

1980 ...

1990 ...

2000 ...

2005 ...

2010 ...

2015 ...

Forum & Blog Postings

1996 ...

2000 ...

2005 ...

2010 ...

Re: Engine Testing - Statistics by John Major, CCC, January 14, 2010

2011

2012

2013

2014

2015 ...

Re: The SPRT without draw model, elo model or whatever.. by Michel Van den Bergh, CCC, August 18, 2016

2016

About expected scores and draw ratios by Jesús Muñoz, CCC, September 17, 2016

2017

Re: MATCH sanity by Salvatore Giannotti, CCC, May 03, 2017
ELO measurements by Peter Österlund, CCC, August 06, 2017 » Playing Strength
Re: "Intrinsic Chess Ratings" by Regan, Haworth -- by Kenneth Regan, CCC, November 20, 2017 » Who is the Master?

2018

2019

External Links

Rating Systems

Tools

Statistics

SPRT

Data Visualization

Misc

ARMS Charity Concert, Madison Square Garden, December 08, 1983

References

  1. ↑ Image based on Standard deviation diagram by Mwtoews, April 7, 2007 with R code given, CC BY 2.5, Wikimedia Commons, Normal distribution from Wikipedia
  2. ↑ Kirr's Chess Engine Comparison KCEC - Draw rate » KCEC
  3. ↑ Doubling of time control by Andreas Strangmüller, CCC, October 21, 2016
  4. ↑ K93-Doubling-TC.pdf
  5. ↑ Scaling at 2x nodes (or doubling time control) by Kai Laskos, CCC, July 23, 2013
  6. ↑ Re: Likelihood Of Success (LOS) in the real world by Álvaro Begué, CCC, May 26, 2017
  7. ↑ Re: Calculating the LOS (likelihood of superiority) from results by Rémi Coulom, CCC, January 23, 2014
  8. ↑ Re: Calculating the LOS (likelihood of superiority) from results by Kai Laskos, CCC, January 22, 2014
  9. ↑ Re: Likelihood of superiority by Rémi Coulom, CCC, November 15, 2009
  10. ↑ Re: Likelihood of superiority by Rémi Coulom, CCC, November 15, 2009
  11. ↑ Error function from Wikipedia
  12. ↑ The Open Group Base Specifications Issue 6IEEE Std 1003.1, 2004 Edition: erf
  13. ↑ erf(x) and math.h by user76293, Stack Overflow, March 10, 2009
  14. ↑ Re: Calculating the LOS (likelihood of superiority) from results by Álvaro Begué, CCC, January 22, 2014
  15. ↑ Error margins via resampling (jackknifing) by Kai Laskos, CCC, August 12, 2016
  16. ↑ Properties of unbalanced openings using Bayeselo model by Kai Laskos, CCC, August 27, 2016
  17. ↑ Abraham Wald (1945). Sequential Tests of Statistical Hypotheses. Annals of Mathematical Statistics, Vol. 16, No. 2, doi: 10.1214/aoms/1177731118
  18. ↑ Sequential probability ratio test from Wikipedia
  19. ↑ Arthur Guez (2015). Sample-based Search Methods for Bayes-Adaptive Planning. Ph.D. thesis, Gatsby Computational Neuroscience Unit, University College London, pdf
  20. ↑ Jack Good (1979). Studies in the history of probability and statistics. XXXVII AM Turing’s statistical work in World War II. Biometrika, Vol. 66, No. 2
  21. ↑ How (not) to use SPRT ? by BB+, OpenChess Forum, October 19, 2013
  22. ↑ Re: The SPRT without draw model, elo model or whatever.. by Michel Van den Bergh, CCC, August 18, 2016
  23. ↑ GSPRT approximation (pdf) by Michel Van den Bergh
  24. ↑ Re: Stockfish Reverts 5 Recent Patches by Michel Van den Bergh, CCC, February 02, 2020
  25. ↑ GitHub - vdbergh/pentanomial: SPRT for pentanomial frequencies and simulation tools by Michel Van den Bergh
  26. ↑ Re: Stockfish Reverts 5 Recent Patches by Michel Van den Bergh, CCC, February 02, 2020
  27. ↑ GitHub - vdbergh/simul: A multi-threaded pentanomial simulator by Michel Van den Bergh
  28. ↑ Law of comparative judgment - Wikipedia
  29. ↑ Elo's Book: The Rating of Chess Players by Sam Sloan
  30. ↑ The Master Game from Wikipedia
  31. ↑ Handwritten Notes on the 2004 David R. Hunter Paper 'MM Algorithms for Generalized Bradley-Terry Models' by Rémi Coulom
  32. ↑ Derivation of bayeselo formula by Rémi Coulom, CCC, August 07, 2012
  33. ↑ Mm algorithm from Wikipedia
  34. ↑ Pairwise comparison from Wikipedia
  35. ↑ Bayesian inference from Wikipedia
  36. ↑ How I did it: Diogo Ferreira on 4th place in Elo chess ratings competition | no free hunch
  37. ↑ "Intrinsic Chess Ratings" by Regan, Haworth -- seq by Kai Middleton, CCC, November 19, 2017
  38. ↑ Re: EloStat, Bayeselo and Ordo by Rémi Coulom, CCC, June 25, 2012
  39. ↑ Re: Understanding and Pushing the Limits of the Elo Rating Algorithm by Daniel Shawul, CCC, October 15, 2019
  40. ↑ Ordo by Miguel A. Ballicora
  41. ↑ Pairwise Analysis of Chess Engine Move Selections by Adam Hair, CCC, April 17, 2011
  42. ↑ Questions regarding rating systems of humans and engines by Erik Varend, CCC, December 06, 2014
  43. ↑ chess statistics scientific article by Nuno Sousa, CCC, July 06, 2016
  44. ↑ Understanding and Pushing the Limits of the Elo Rating Algorithm by Michel Van den Bergh, CCC, October 15, 2019
  45. ↑ LOS Table by Joseph Ciarrochi from CEGT
  46. ↑ Arpad Elo and the Elo Rating System by Dan Ross, ChessBase News, December 16, 2007
  47. ↑ David R. Hunter (2004). MM Algorithms for Generalized Bradley-Terry Models. The Annals of Statistics, Vol. 32, No. 1, 384–406, pdf
  48. ↑ Type I and type II errors from Wikipedia
  49. ↑ Arpad Elo - Wikipedia
  50. ↑ Regan's latest: Depth of Satisficing by Carl Lumma, CCC, October 09, 2015
  51. ↑ Resampling (statistics) from Wikipedia
  52. ↑ Jackknife resampling from WIkipedia
  53. ↑ Delphil 3.3b2 (2334) - Stockfish 030916 (3228), TCEC Season 9 - Rapid, Round 11, September 16, 2016
  54. ↑ World Chess Championship 2016 from Wikipedia
  55. ↑ Normalized Elo (pdf) by Michel Van den Bergh
  56. ↑ table for detecting significant difference between two engines by Joseph Ciarrochi, CCC, February 03, 2006
  57. ↑ an interesting study from Erik Varend by scandien, Hiarcs Forum, August 13, 2017
  58. ↑ A Visual Look at 2 Million Chess Games by Brahim Hamadicharef, CCC, November 02, 2017

Up one level

Retrieved from "https://www.chessprogramming.org/index.php?title=Match_Statistics&oldid=17846"