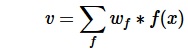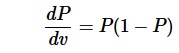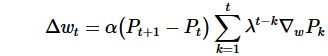Temporal Difference Learning
Home * Learning * Temporal Difference Learning
Temporal Difference Learning, (TD learning)
is a machine learning method applied to multi-step prediction problems. As a prediction method primarily used for reinforcement learning, TD learning takes into account the fact that subsequent predictions are often correlated in some sense, while in supervised learning, one learns only from actually observed values. TD resembles Monte Carlo methods with dynamic programming techniques [1]. In the domain of computer games and computer chess, TD learning is applied through self play, subsequently predicting the probability of winning a game during the sequence of moves from the initial position until the end, to adjust weights for a more reliable prediction.
Contents
Prediction
Each prediction is a single number, derived from a formula using adjustable weights of features, for instance a neural network most simply a single neuron perceptron, that is a linear evaluation function ...
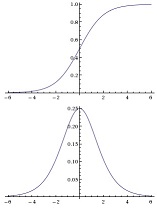
... with the pawn advantage converted to a winning probability by the standard sigmoid squashing function, also topic in logistic regression in the domain of supervised learning and automated tuning, ...
... which has the advantage of its simple derivative:
TD(λ)
Each pair of temporally successive predictions P at time step t and t+1 gives rise to a recommendation for weight changes, to converge Pt to Pt+1, first applied in the late 50s by Arthur Samuel in his Checkers player for automamated evaluation tuning [2]. This TD method was improved, generalized and formalized by Richard Sutton et al. in the 80s, the term Temporal Difference Learning coined in 1988 [3], also introducing the decay or recency parameter λ, where proportions of the score came from the outcome of Monte Carlo simulated games, tapering between bootstrapping (λ = 0) and Monte Carlo predictions (λ = 1), the latter equivalent to gradient descent on the mean squared error function. Weight adjustments in TD(λ) are made according to ...
... where P is the series of temporally successive predictions, w the set of adjustable weights. α is a parameter controlling the learning rate, also called step-size, ∇wPk [4] is the gradient, the vector of partial derivatives of Pt with respect of w. The process may be applied to any initial set of weights. Learning performance depends on λ and α, which have to be chosen appropriately for the domain. In principle, TD(λ) weight adjustments may be made after each move, or at any arbitrary interval. For game playing tasks the end of every game is a convenient point to actually alter the evaluation weights [5].
TD(λ) was famously applied by Gerald Tesauro in his Backgammon program TD-Gammon [6] [7], a stochastic game picking the action whose successor state minimizes the opponent's expected reward, i.e. looking one ply ahead.
TDLeaf(λ)
In games like chess or Othello, due to their tactical nature, deep searches are necessary for expert performance. The problem has already been recognized and solved by Arthur Samuel but seemed to have been forgotten later on [8] - rediscovered independently by Don Beal and Martin C. Smith in 1997 [9], and by Jonathan Baxter, Andrew Tridgell, and Lex Weaver [10], who coined the term TD-Leaf. TD-Leaf is the adaption of TD(λ) to minimax search, where instead of the corresponding positions of the root the leaf nodes of the principal variation are considered in the weight adjustments. TD-Leaf was successfully used in evaluation tuning of chess programs [11], with KnightCap [12] and CilkChess as most prominent samples, while the latter used the improved Temporal Coherence Learning [13], which automatically adjusts α and λ [14].
Quotes
Don Beal
Don Beal in a 1998 CCC discussion with Jonathan Baxter [15]:
With fixed learning rates (aka step size) we found piece values settle to consistent relative ordering in around 500 self-play games. The ordering remains in place despite considerable erratic movements. But piece-square values can take a lot longer - more like 5000.
The learning rate is critical - it has to be as large as one dares for fast learning, but low for stable values. We've been experimenting with methods for automatically adjusting the learning rate. (Higher rates if the adjustments go in the same direction, lower if they keep changing direction.)
The other problem is learning weights for terms which only occur rarely. Then the learning process doesn't see enough examples to settle on good weights in a reasonable time. I suspect this is the main limitation of the method, but it may be possible to devise ways to generate extra games which exercise the rare conditions.
Bas Hamstra
Bas Hamstra in a 2002 CCC discussion on TD learning [16]:
I have played with it. I am convinced it has possibilities, but one problem I encountered was the cause-effect problem. For say I am a piece down. After I lost the game TD will conclude that the winner had better mobility and will tune it up. However worse mobility was not the cause of the loss, it was the effect of simply being a piece down. In my case it kept tuning mobility up and up until ridiculous values.
Don Dailey
Don Dailey in a reply [17] to Ben-Hur Carlos Vieira Langoni Junior, CCC, December 2010 [18] :
Another approach that may be more in line with what you want is called "temporal difference learning", and it is based on feedback from each move to the move that precedes it. For example if you play move 35 and the program thinks the position is equal, but then on move 36 you find that you are winning a pawn, it indicates that the evaluation of move 35 is in error, the position is better than the program thought it was. Little tiny incremental adjustments are made to the evaluation function so that it is ever so slightly biased in favor of being slightly more positive in this case, or slightly more negative in the case where you find your score is dropping. This is done recursively back through the moves of the game so that winning the game gives some credit to all the positions of the game. Look on the web and read up on the "credit assignment problem" and temporal difference learning. It's probably ideal for what you are looking for. It can be done at the end of the game one time and scores then updated. If you are not using floating point evaluation you may have to figure out how to modify this to be workable.
Chess Programs
See also
Publications
1959
- Arthur Samuel (1959). Some Studies in Machine Learning Using the Game of Checkers. IBM Journal July 1959
1970 ...
- A. Harry Klopf (1972). Brain Function and Adaptive Systems - A Heterostatic Theory. Air Force Cambridge Research Laboratories, Special Reports, No. 133, pdf
- John H. Holland (1975). Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. amazon.com
- Ian H. Witten (1977). An Adaptive Optimal Controller for Discrete-Time Markov Environments. Information and Control, Vol. 34, No. 4, pdf
1980 ...
- Richard Sutton (1984). Temporal Credit Assignment in Reinforcement Learning. Ph.D. dissertation, University of Massachusetts
- Jens Christensen (1986). Learning Static Evaluation Functions by Linear Regression. in Tom Mitchell, Jaime Carbonell, Ryszard Michalski (1986). Machine Learning: A Guide to Current Research. The Kluwer International Series in Engineering and Computer Science, Vol. 12
- Richard Sutton (1988). Learning to Predict by the Methods of Temporal Differences. Machine Learning, Vol. 3, No. 1
- Andrew Barto, Richard Sutton, Christopher J. C. H. Watkins (1989). Sequential Decision Problems and Neural Networks. NIPS 1989
1990 ...
- Richard Sutton, Andrew Barto (1990). Time-Derivative Models of Pavlovian Reinforcement. in Michael Gabriel, John Moore (eds.) (1990). Learning and Computational Neuroscience: Foundations of Adaptive Networks. MIT Press, pdf
- Richard C. Yee, Sharad Saxena, Paul E. Utgoff, Andrew Barto (1990). Explaining Temporal Differences to Create Useful Concepts for Evaluating States. AAAI 1990, pdf
- Peter Dayan (1990). Navigating Through Temporal Difference. NIPS 1990
- Gerald Tesauro (1992). Temporal Difference Learning of Backgammon Strategy. ML 1992
- Peter Dayan (1992). The convergence of TD (λ) for general λ. Machine Learning, Vol. 8, No. 3
- Gerald Tesauro (1992). Practical Issues in Temporal Difference Learning. Machine Learning, Vol. 8, Nos. 3-4
- Michael Gherrity (1993). A Game Learning Machine. Ph.D. thesis, University of California, San Diego, advisor Paul Kube, pdf, pdf
- Peter Dayan (1993). Improving generalisation for temporal difference learning: The successor representation. Neural Computation, Vol. 5, pdf
- Nicol N. Schraudolph, Peter Dayan, Terrence J. Sejnowski (1993). Temporal Difference Learning of Position Evaluation in the Game of Go. NIPS 1993 [20]
- Peter Dayan, Terrence J. Sejnowski (1994). TD(λ) converges with Probability 1. Machine Learning, Vol. 14, No. 1, pdf
1995 ...
- Anton Leouski (1995). Learning of Position Evaluation in the Game of Othello. Master's Project, University of Massachusetts, Amherst, Massachusetts, pdf
- Gerald Tesauro (1995). Temporal Difference Learning and TD-Gammon. Communications of the ACM, Vol. 38, No. 3
- Sebastian Thrun (1995). Learning to Play the Game of Chess. in Gerald Tesauro, David S. Touretzky, Todd K. Leen (eds.) Advances in Neural Information Processing Systems 7, MIT Press
1996
- Robert Schapire, Manfred K. Warmuth (1996). On the Worst-Case Analysis of Temporal-Difference Learning Algorithms. Machine Learning, Vol. 22, Nos. 1-3, pdf
- Johannes Fürnkranz (1996). Machine Learning in Computer Chess: The Next Generation. ICCA Journal, Vol. 19, No. 3, zipped ps
- Steven Bradtke, Andrew Barto (1996) Linear Least-Squares Algorithms for Temporal Difference Learning. Machine Learning, Vol. 22, Nos. 1/2/3, pdf
1997
- John N. Tsitsiklis, Benjamin Van Roy (1997). An Analysis of Temporal Difference Learning with Function Approximation. IEEE Transactions on Automatic Control, Vol. 42, No. 5
- Don Beal, Martin C. Smith (1997). Learning Piece Values Using Temporal Differences. ICCA Journal, Vol. 20, No. 3
- Jonathan Baxter, Andrew Tridgell, Lex Weaver (1997) Knightcap: A chess program that learns by combining td(λ) with minimax search. 15th International Conference on Machine Learning, pdf via citeseerX
1998
- Don Beal, Martin C. Smith (1998). First Results from Using Temporal Difference Learning in Shogi. CG 1998
- Jonathan Baxter, Andrew Tridgell, Lex Weaver (1998). Experiments in Parameter Learning Using Temporal Differences. ICCA Journal, Vol. 21, No. 2
- Richard Sutton, Andrew Barto (1998). Reinforcement Learning: An Introduction. MIT Press, 6. Temporal-Difference Learning
- Justin A. Boyan (1998). Least-Squares Temporal Difference Learning. Carnegie Mellon University, CMU-CS-98-152, pdf
1999
- Jonathan Baxter, Andrew Tridgell, Lex Weaver (1999). TDLeaf(lambda): Combining Temporal Difference Learning with Game-Tree Search. Australian Journal of Intelligent Information Processing Systems, Vol. 5 No. 1, arXiv:cs/9901001
- Don Beal, Martin C. Smith (1999). Temporal Coherence and Prediction Decay in TD Learning. IJCAI 1999, pdf
- Don Beal, Martin C. Smith (1999). Learning Piece-Square Values using Temporal Differences. ICCA Journal, Vol. 22, No. 4
2000 ...
- Sebastian Thrun, Michael L. Littman (2000). A Review of Reinforcement Learning. AI Magazine, Vol. 21, No. 1, pdf
- Robert Levinson, Ryan Weber (2000). Chess Neighborhoods, Function Combination, and Reinforcement Learning. CG 2000, pdf » Morph
- Jonathan Baxter, Andrew Tridgell, Lex Weaver (2000). Learning to Play Chess Using Temporal Differences. Machine Learning, Vol 40, No. 3, pdf
- Johannes Fürnkranz (2000). Machine Learning in Games: A Survey. Austrian Research Institute for Artificial Intelligence, OEFAI-TR-2000-3, pdf
2001
- Jonathan Schaeffer, Markian Hlynka, Vili Jussila (2001). Temporal Difference Learning Applied to a High-Performance Game-Playing Program. IJCAI 2001
- Don Beal, Martin C. Smith (2001). Temporal difference learning applied to game playing and the results of application to Shogi. Theoretical Computer Science, Vol. 252, Nos. 1-2
- Nicol N. Schraudolph, Peter Dayan, Terrence J. Sejnowski (2001). Learning to Evaluate Go Positions via Temporal Difference Methods. Computational Intelligence in Games, Studies in Fuzziness and Soft Computing. Physica-Verlag, pdf
- Lex Weaver, Jonathan Baxter (2001). STD (λ): learning state differences with TD (λ). CiteSeerX
2002
- Ari Shapiro, Gil Fuchs, Robert Levinson (2002). Learning a Game Strategy Using Pattern-Weights and Self-play. CG 2002, pdf
- Mark Winands, Levente Kocsis, Jos Uiterwijk, Jaap van den Herik (2002). Temporal difference learning and the Neural MoveMap heuristic in the game of Lines of Action. GAME-ON 2002 » Neural MoveMap Heuristic
- James Swafford (2002). Optimizing Parameter Learning using Temporal Differences. AAAI-02, Student Abstracts, pdf
- Justin A. Boyan (2002). Technical Update: Least-Squares Temporal Difference Learning. Machine Learning, Vol. 49, pdf
- Don Beal (2002). TD(µ): A Modification of TD(λ) That Enables a Program to Learn Weights for Good Play Even if It Observes Only Bad Play. JCIS 2002
2003
- Henk Mannen (2003). Learning to play chess using reinforcement learning with database games. Master’s thesis, Cognitive Artificial Intelligence, Utrecht University
2004
- Henk Mannen, Marco Wiering (2004). Learning to play chess using TD(λ)-learning with database games. Cognitive Artificial Intelligence, Utrecht University, Benelearn’04
- Marco Block (2004). Verwendung von Temporale-Differenz-Methoden im Schachmotor FUSc#. Diplomarbeit, Betreuer: Raúl Rojas, Free University of Berlin, pdf (German)
- Jacek Mańdziuk, Daniel Osman (2004). Temporal Difference Approach to Playing Give-Away Checkers. ICAISC 2004, pdf
2005 ...
- Marco Wiering, Jan Peter Patist, Henk Mannen (2005). Learning to Play Board Games using Temporal Difference Methods. Technical Report, Utrecht University, UU-CS-2005-048, pdf
- Thomas Philip Runarsson, Simon Lucas (2005). Coevolution versus self-play temporal difference learning for acquiring position evaluation in small-board go. IEEE Transactions on Evolutionary Computation, Vol. 9, No. 6
2006
- Simon Lucas, Thomas Philip Runarsson (2006). Temporal Difference Learning versus Co-Evolution for Acquiring Othello Position Evaluation. CIG 2006
2007
- Edward P. Manning (2007). Temporal Difference Learning of an Othello Evaluation Function for a Small Neural Network with Shared Weights. IEEE Symposium on Computational Intelligence and AI in Games
- Daniel Osman (2007). Temporal Difference Methods for Two-player Board Games. Ph.D. thesis, Faculty of Mathematics and Information Science, Warsaw University of Technology
- Yasuhiro Osaki, Kazutomo Shibahara, Yasuhiro Tajima, Yoshiyuki Kotani (2007). Reinforcement Learning of Evaluation Functions Using Temporal Difference-Monte Carlo learning method. 12th Game Programming Workshop
- Andrew Barto (2007). Temporal difference learning. Scholarpedia 2(11):1604
2008
- Yasuhiro Osaki, Kazutomo Shibahara, Yasuhiro Tajima, Yoshiyuki Kotani (2008). An Othello Evaluation Function Based on Temporal Difference Learning using Probability of Winning. CIG'08, pdf
- Richard Sutton, Csaba Szepesvári, Hamid Reza Maei (2008). A Convergent O(n) Algorithm for Off-policy Temporal-difference Learning with Linear Function Approximation. NIPS 2008, pdf
- Sacha Droste, Johannes Fürnkranz (2008). Learning of Piece Values for Chess Variants. Technical Report TUD–KE–2008-07, Knowledge Engineering Group, TU Darmstadt, pdf
- Sacha Droste, Johannes Fürnkranz (2008). Learning the Piece Values for three Chess Variants. ICGA Journal, Vol. 31, No. 4
- Marco Block, Maro Bader, Ernesto Tapia, Marte Ramírez, Ketill Gunnarsson, Erik Cuevas, Daniel Zaldivar, Raúl Rojas (2008). Using Reinforcement Learning in Chess Engines. Concibe Science 2008, Research in Computing Science: Special Issue in Electronics and Biomedical Engineering, Computer Science and Informatics, Vol. 35, pdf
- Albrecht Fiebiger (2008). Einsatz von allgemeinen Evaluierungsheuristiken in Verbindung mit der Reinforcement-Learning-Strategie in der Schachprogrammierung. Besondere Lernleistung im Fachbereich Informatik, Sächsischees Landesgymnasium Sankt Afra, Internal advisor: Ralf Böttcher, External advisors: Stefan Meyer-Kahlen, Marco Block, pdf (German)
2009
- Hamid Reza Maei, Csaba Szepesvári, Shalabh Bhatnagar, Doina Precup, David Silver, Richard Sutton (2009). Convergent Temporal-Difference Learning with Arbitrary Smooth Function Approximation. NIPS 2009, pdf
- Joel Veness, David Silver, William Uther, Alan Blair (2009). Bootstrapping from Game Tree Search. NIPS 2009, pdf
- Richard Sutton, Hamid Reza Maei, Doina Precup, Shalabh Bhatnagar, David Silver, Csaba Szepesvári, Eric Wiewiora. (2009). Fast Gradient-Descent Methods for Temporal-Difference Learning with Linear Function Approximation. ICML 2009
- Simon Lucas (2009). Temporal difference learning with interpolated table value functions. CIG 2009
- Marcin Szubert, Wojciech Jaśkowski, Krzysztof Krawiec (2009). Coevolutionary Temporal Difference Learning for Othello. GIG 2009, pdf
- Marcin Szubert (2009). Coevolutionary Reinforcement Learning and its Application to Othello. M.Sc. thesis, Poznań University of Technology, supervisor Krzysztof Krawiec, pdf
- J. Zico Kolter, Andrew Ng (2009). Regularization and Feature Selection in Least-Squares Temporal Difference Learning. ICML 2009, pdf
2010 ...
- Marco Wiering (2010). Self-play and using an expert to learn to play backgammon with temporal difference learning. Journal of Intelligent Learning Systems and Applications, Vol. 2, No. 2
- Hamid Reza Maei, Richard Sutton (2010). GQ(λ): A general gradient algorithm for temporal-difference prediction learning with eligibility traces. AGI 2010
- Hamid Reza Maei (2011). Gradient Temporal-Difference Learning Algorithms. Ph.D. thesis, University of Alberta, advisor Richard Sutton
- Joel Veness (2011). Approximate Universal Artificial Intelligence and Self-Play Learning for Games. Ph.D. thesis, University of New South Wales, supervisors: Kee Siong Ng, Marcus Hutter, Alan Blair, William Uther, John Lloyd; pdf
- I-Chen Wu, Hsin-Ti Tsai, Hung-Hsuan Lin, Yi-Shan Lin, Chieh-Min Chang, Ping-Hung Lin (2011). Temporal Difference Learning for Connect6. Advances in Computer Games 13
- Nikolaos Papahristou, Ioannis Refanidis (2011). Improving Temporal Difference Performance in Backgammon Variants. Advances in Computer Games 13, pdf
- Krzysztof Krawiec, Wojciech Jaśkowski, Marcin Szubert (2011). Evolving small-board Go players using Coevolutionary Temporal Difference Learning with Archives. Applied Mathematics and Computer Science, Vol. 21, No. 4
- Marcin Szubert, Wojciech Jaśkowski, Krzysztof Krawiec (2011). Learning Board Evaluation Function for Othello by Hybridizing Coevolution with Temporal Difference Learning. Control and Cybernetics, Vol. 40, No. 3, pdf
- István Szita (2012). Reinforcement Learning in Games. in Marco Wiering, Martijn Van Otterlo (eds.). Reinforcement learning: State-of-the-art. Adaptation, Learning, and Optimization, Vol. 12, Springer
- David Silver, Richard Sutton, Martin Mueller (2013). Temporal-Difference Search in Computer Go. Proceedings of the ICAPS-13 Workshop on Planning and Learning, pdf
- Florian Kunz (2013). An Introduction to Temporal Difference Learning. Seminar on Autonomous Learning Systems, TU Darmstad, pdf
- I-Chen Wu, Kun-Hao Yeh, Chao-Chin Liang, Chia-Chuan Chang, Han Chiang (2014). Multi-Stage Temporal Difference Learning for 2048. TAAI 2014
- Wojciech Jaśkowski, Marcin Szubert, Paweł Liskowski (2014). Multi-Criteria Comparison of Coevolution and Temporal Difference Learning on Othello. EvoApplications 2014, Springer, volume 8602
2015 ...
- James L. McClelland (2015). Explorations in Parallel Distributed Processing: A Handbook of Models, Programs, and Exercises. Second Edition, Contents, Temporal-Difference Learning
- Matthew Lai (2015). Giraffe: Using Deep Reinforcement Learning to Play Chess. M.Sc. thesis, Imperial College London, arXiv:1509.01549v1 » Giraffe
- Markus Thill (2015). Temporal Difference Learning Methods with Automatic Step-Size Adaption for Strategic Board Games: Connect-4 and Dots-and-Boxes. Master thesis, Technical University of Cologne, Campus Gummersbach, pdf
- Kazuto Oka, Kiminori Matsuzaki (2016). Systematic Selection of N-tuple Networks for 2048. CG 2016
- Huizhen Yu, A. Rupam Mahmood, Richard Sutton (2017). On Generalized Bellman Equations and Temporal-Difference Learning. Canadian Conference on AI 2017, arXiv:1704.04463
- William Uther (2017). Temporal Difference Learning. in Claude Sammut, Geoffrey I. Webb (eds) (2017). Encyclopedia of Machine Learning and Data Mining. Springer
2020 ...
- Emmanuel Bengio, Joelle Pineau, Doina Precup (2020). Interference and Generalization in Temporal Difference Learning. arXiv:2003.06350
- Joshua Romoff, Peter Henderson, David Kanaa, Emmanuel Bengio, Ahmed Touati, Pierre-Luc Bacon, Joelle Pineau (2020). TDprop: Does Jacobi Preconditioning Help Temporal Difference Learning? arXiv:2007.02786
Forum Posts
1995 ...
- Parameter Tuning by Jonathan Baxter, CCC, October 01, 1998 » KnightCap
- Re: Parameter Tuning by Don Beal, CCC, October 02, 1998
2000 ...
- Pseudo-code for TD learning by Daniel Homan, CCC, July 06, 2000
- any good experiences with genetic algos or temporal difference learning? by Rafael B. Andrist, CCC, January 01, 2001
- Temporal Difference by Bas Hamstra, CCC, January 05, 2001
- Tao update by Bas Hamstra, CCC, January 12, 2001 » Tao
- Re: Parameter Learning Using Temporal Differences ! by Aaron Tay, CCC, March 19, 2002
- Hello from Edmonton (and on Temporal Differences) by James Swafford, CCC, July 30, 2002
- Temporal Differences by Stuart Cracraft, CCC, November 03, 2004
- Re: Temporal Differences by Guy Haworth, CCC, November 04, 2004 [21]
- Temporal Differences by Peter Fendrich, CCC, December 21, 2004
- Chess program improvement project (copy at TalkChess/ICD) by Stuart Cracraft, Winboard Forum, March 07, 2006 » Win at Chess
2010 ...
- Positional learning by Ben-Hur Carlos Vieira Langoni Junior, CCC, December 13, 2010
- Re: Positional learning by Don Dailey, CCC, December 13, 2010
- Pawn Advantage, Win Percentage, and Elo by Adam Hair, CCC, April 15, 2012
- Re: Pawn Advantage, Win Percentage, and Elo by Don Dailey, CCC, April 15, 2012
2015 ...
- *First release* Giraffe, a new engine based on deep learning by Matthew Lai, CCC, July 08, 2015 » Deep Learning, Giraffe
- td-leaf by Alexandru Mosoi, CCC, October 06, 2015 » Automated Tuning
- TD-leaf(lambda) by Robert Pope, CCC, November 09, 2016
- TD(1) by Rémi Coulom, Game-AI Forum, November 20, 2019 » Automated Tuning
2020 ...
- Board adaptive / tuning evaluation function - no NN/AI by Moritz Gedig, CCC, January 14, 2020
- TD learning by self play (TD-Gammon) by Chris Whittington, CCC, April 10, 2021
External Links
- Reinforcement learning - Temporal difference methods from Wikipedia
- Standing on the shoulders of giants by Albert Silver, ChessBase News, September 18, 2019
- Shawn Lane, Jonas Hellborg, Jeff Sipe - Temporal Analogues of Paradise, YouTube Video
References
- ↑ Temporal difference learning from Wikipedia
- ↑ Arthur Samuel (1959). Some Studies in Machine Learning Using the Game of Checkers. IBM Journal July 1959
- ↑ Richard Sutton (1988). Learning to Predict by the Methods of Temporal Differences. Machine Learning, Vol. 3, No. 1, pdf
- ↑ Nabla symbol from Wikipedia
- ↑ Don Beal, Martin C. Smith (1998). First Results from Using Temporal Difference Learning in Shogi. CG 1998
- ↑ Gerald Tesauro (1992). Temporal Difference Learning of Backgammon Strategy. ML 1992
- ↑ Gerald Tesauro (1994). TD-Gammon, a Self-Teaching Backgammon Program, Achieves Master-Level Play. Neural Computation Vol. 6, No. 2
- ↑ Sacha Droste, Johannes Fürnkranz (2008). Learning of Piece Values for Chess Variants. Technical Report TUD–KE–2008-07, Knowledge Engineering Group, TU Darmstadt, pdf
- ↑ Don Beal, Martin C. Smith (1997). Learning Piece Values Using Temporal Differences. ICCA Journal, Vol. 20, No. 3
- ↑ Jonathan Baxter, Andrew Tridgell, Lex Weaver (1997) Knightcap: A chess program that learns by combining td(λ) with minimax search. 15th International Conference on Machine Learning, pdf via citeseerX
- ↑ Don Beal, Martin C. Smith (1999). Learning Piece-Square Values using Temporal Differences. ICCA Journal, Vol. 22, No. 4
- ↑ Jonathan Baxter, Andrew Tridgell, Lex Weaver (1998). Knightcap: A chess program that learns by combining td(λ) with game-tree search. Proceedings of the 15th International Conference on Machine Learning, pdf via citeseerX
- ↑ The Cilkchess Parallel Chess Program
- ↑ Don Beal, Martin C. Smith (1999). Temporal Coherence and Prediction Decay in TD Learning. IJCAI 1999, pdf
- ↑ Re: Parameter Tuning by Don Beal, CCC, October 02, 1998
- ↑ Re: Hello from Edmonton (and on Temporal Differences) by Bas Hamstra, CCC, August 05, 2002
- ↑ Re: Positional learning by Don Dailey, CCC, December 13, 2010
- ↑ Positional learning by Ben-Hur Carlos Vieira Langoni Junior, CCC, December 13, 2010
- ↑ Tao update by Bas Hamstra, CCC, January 12, 2001
- ↑ Nici Schraudolph’s go networks, review by Jay Scott
- ↑ Guy Haworth, Meel Velliste (1998). Chess Endgames and Neural Networks. ICCA Journal, Vol. 21, No. 4