Morph
Morph [2],
a research chess program started by Robert Levinson in 1989 at University of California, Santa Cruz with the goal to create an autonomous chess learner, knowing only the rules of chess and then evolve from game to game using heuristics derived from machine learning algorithms such as pattern recognition, temporal difference learning and neural networks. It uses a graph representation of chess positions and pattern-oriented databases in conjunction with minimax search. Research has been done by dedicated undergraduate volunteers at UCSC, most computer science students with interests in chess and Artificial Intelligence [3].
Contents
Morph's History
Morph I/II
The project began with the goal of developing a chess program that conformed more to cognitive models of human chess playing than conventional chess programs. The key idea was to make the program adaptive and pattern-oriented, limited to searching only one ply and to acquiering its own chess knowledge through experience - assisted by a human-designed graph-theoretic representation language for chess patterns.
Morph stores its experience as <pattern, weight> pairs (pws). Morph's pattern are directed graphs where the nodes represent pieces and squares sorrounding the king and the edges represent (X-ray) attacks or defenses. To evaluate a position, Morph finds which graphs in the database match that position and then combines the weights associated with each graph. At the end of each game, Morph uses temporal difference learning to adjust the weights of the pattern that match each position in the game. In addition, Morph creates new patterns that should enable it to determine more accurately the value of that or similar positions should it occur in the future.
The utility of pattern can be measured by the variance in its sequence of weights, which is maintained incrementally by storing the number of updates and accumulating the absolute value of their weight changes, used to decide whether patterns are deleted. After training and improving in about 3000 to 4000 games against GNU Chess, Morph I was able to defeat human chess novices while searching just one ply [4] [5]. Morph II is a generalization of Morph's learning and pattern representation to be applicable to most two-player games and search problems given the rules of those domains.
Morph III/IV
The Morph III architecture allows for any reasonable number of knowledge sources to be used, a concept similar to that of advisors in the Hoyle system by Susan L. Epstein [6]. Compared to Morph I which had a bag of pattern, Morph's representation shifted towards learning internal weights. Morph III and Morph IV used nearest neighbor and decision trees to divide positions into equivalence classes and query them on-line in logarithmic time. However these approaches require a large amount of training data to achieve reasonable levels of play.
Morph V
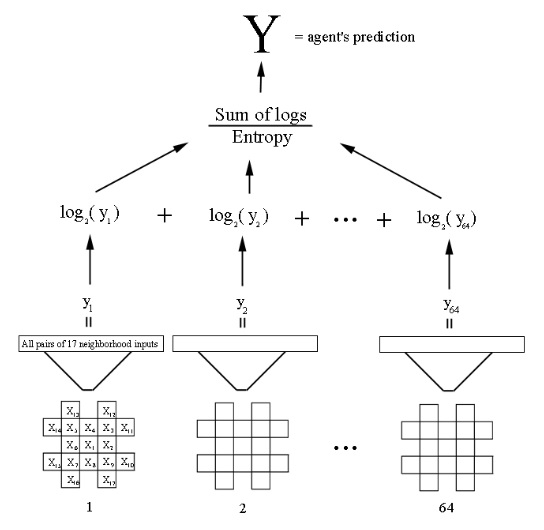
Latest Morph, as mentioned in 2004 [7], uses a unique chess board representation called Chess Neighborhood [8] and uses a regression network to learn nonlinear combinations of the individual values of pieces that make up a piece neighborhood to arrive at a single value for the entire neighborhood. A vector of 64 neighborhoods of each square is suited to serve as an input layer of the regression network, whose weights are optimized by gradient descent, along with training positions previously generated using temporal difference learning. At the lower level the expected probability of winning of the neighborhoods are learned and at the top they are combined based on their product and entropy.
The overall model of the Morph learner [9]
See also
Publications
1989
- Robert Levinson (1989). A Self-Learning, Pattern-Oriented Chess Program. WCCC 1989 - Workshop on New Directions in Game-Tree Search
- Robert Levinson (1989). A Self-Learning, Pattern-Oriented Chess Program. ICCA Journal, Vol. 12, No. 4
1990 ...
- Robert Levinson, Brian Beach, Richard Snyder, Tal Dayan, Kirack Sohn (1990). Adaptive-predictive game-playing programs. abstract
- Robert Levinson (1991). A Self-Organizing Pattern Retrieval System and its Applications. International Journal of Intelligent Systems, Vol. 6, pp. 717-738. ISSN 0884-8173.
- Robert Levinson, Richard Snyder (1991). Adaptive Pattern-Oriented Chess. Proceedings of the 8th International Workshop on Machine Learning (eds. L. Birnbaum and G. Collins), pp. 85-89. Morgan Kaufmann, San Mateo, CA. Also published in: Proceedings of the Ninth National Conference on Artificial Intelligence AAAI-91, pp. 601-606. AAAI Press, MIT Press, Boston, MA. pdf
- Robert Levinson, John Amenta (1993). MORPH, An Experience-Based Adaptive Chess System. ICCA Journal, Vol. 16, No. 1 [10]
- Robert Levinson, Richard Snyder (1993). Distance: Toward the Unification of Chess Knowledge. ICCA Journal, Vol. 16, No. 3 » WCCC 1992 - Workshop
- Jeffrey Gould, Robert Levinson (1994). Experience-Based Adaptive Search. Machine Learning: A Multi-Strategy Approach (eds. R. Michalski and G. Tecuci), Vol. 4
- Robert Levinson, Gil Fuchs (1994). A Pattern-Weight Formulation of Search Knowledge. UCSC-CRL-94-10, CiteSeerX
- Robert Levinson (1994). Morph II: A Universal Agent: Progess Report and Proposal. UCSC-CRL-94-22
- Robert Levinson (1996). General Game-Playing and Reinforcement Learning. Computational Intelligence, Vol. 12, No. 1
- Jonathan Allen, Edward Hamilton, Robert Levinson (1997). New Advances in Adaptive Pattern-Oriented Chess. Advances in Computer Chess 8
2000 ...
- Robert Levinson, Ryan Weber (2000). Pattern-Level Temporal Difference-Learning, Data Fusion and Chess. In Sensor Fusion: Architecture, Algorithms, and Applications IV. Orlando, Florida, April 2000
- Robert Levinson, Ryan Weber (2000). Chess Neighborhoods, Function Combination, and Reinforcement Learning. CG 2000, pdf
- Daniel Walker, Robert Levinson (2004). The MORPH Project in 2004. ICGA Journal, Vol. 27, No. 4
Forum Posts
- Computer learning chess from scratch? Morph? by John Michael Sauder, rgcc, April 16, 1996
- morph(C) on ICC by Jeff Anderson, CCC, October 11, 1999
- Re: morph(C) on ICC by Robert Hyatt, CCC, October 12, 1999
- morph(C) -- can this really work ? by Georg von Zimmermann, CCC, October 13, 1999
- Morph lll by K. Burcham, CCC, October 29, 2003
- Re: learning by Denis P. Mendoza, CCC, February 03, 2008
- Re: learning by Shivkumar Shivaji, CCC, February 03, 2008
External Links
Chess Program
- the Morph project by Jay Scott
- Finger morph2 @ ICC
- "Deep Blue" inspires deep thinking about artificial intelligence by computer scientist by Robert Irion, University of California, Santa Cruz, May 5, 1997 [11] » Deep Blue
Misc
- morph - Wiktionary
- -morph - Wiktionary
- Word Root Of The Day: morph | Membean
- Morph from Wikipedia
- Muller's morphs from Wikipedia (amorph, hypomorph, hypermorph, antimorph and neomorph)
- Morpheme from Wikipedia
- Morphine from Wikipedia
- Morphing from Wikipedia
- Morphism from Wikipedia
- Morphism of algebraic varieties from Wikipedia
- Homomorphism from Wikipedia
- Isomorphism from Wikipedia
- Isomorph from Wikipedia
References
- ↑ Robert Levinson photo: 05-05-97 by Don Harris, UCSC Photo Services, in "Deep Blue" inspires deep thinking about artificial intelligence by computer scientist by Robert Irion, CURRENTS, University of California, Santa Cruz, May 5, 1997
- ↑ The name "Morph" comes from the Greek "morph" meaning form and the chess great, Paul Morphy, footnote 1 in Robert Levinson, Richard Snyder (1991). Adaptive Pattern-Oriented Chess. Proceedings of the 8th International Workshop on Machine Learning (eds. L. Birnbaum and G. Collins), pp. 85-89. Morgan Kaufmann, San Mateo, CA. Also published in: Proceedings of the Ninth National Conference on Artificial Intelligence AAAI-91, pp. 601-606. AAAI Press, MIT Press, Boston, MA. pdf
- ↑ Daniel Walker, Robert Levinson (2004). The MORPH Project in 2004. ICGA Journal, Vol. 27, No. 4
- ↑ Robert Levinson, John Amenta (1993). MORPH, An Experience-Based Adaptive Chess System. ICCA Journal, Vol. 16, No. 1
- ↑ Jonathan Allen, Edward Hamilton, Robert Levinson (1997). New Advances in Adaptive Pattern-Oriented Chess. Advances in Computer Chess 8
- ↑ Susan L. Epstein (1992). Prior Knowledge Strengthens Learning to Control Search in Weak Theory Domains. International Journal of Intelligent Systems, Vol. 7, No. 6
- ↑ Daniel Walker, Robert Levinson (2004). The MORPH Project in 2004. ICGA Journal, Vol. 27, No. 4
- ↑ Robert Levinson, Ryan Weber (2000). Chess Neighborhoods, Function Combination, and Reinforcement Learning. CG 2000, pdf
- ↑ Image Fig. 5.3 on pg. 13 from Robert Levinson, Ryan Weber (2000). Chess Neighborhoods, Function Combination, and Reinforcement Learning. CG 2000, pdf
- ↑ reprinted in The 23rd ACM International Computer Chess Championship from The Computer History Museum, pdf
- ↑ Robert Levinson, Jeff Wilkinson (1997). Deep Blue is Still an Infant. AAAI, Technical Report WS-97-04