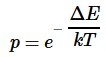Simulated Annealing

From Chessprogramming wiki
Revision as of 18:34, 13 July 2020 by GerdIsenberg (talk | contribs)
Jump to: navigation, search

Home * Programming * Algorithms * Simulated Annealing

Glowing train wheels [1]

Simulated Annealing, (SA)
a Monte Carlo based algorithm for combinatorial optimization problems inspired by statistical mechanics in thermodynamics with the statistical ensemble of the probability distribution over all possible states of a system described by a Markov chain, where its stationary distribution converts to an optimal distribution during a cooling process after reaching the equilibrium. Thus, the annealing algorithm simulates a nonstationary finite state Markov chain whose state space is the domain of the cost function called energy to be minimized [2].

History

The annealing algorithm is an adaptation of the Metropolis–Hastings algorithm to generate sample states of a thermodynamic system, invented by Marshall Rosenbluth and published by Nicholas Metropolis et al. in 1953 [3] [4] , later generalized by W. Keith Hastings at University of Toronto [5]. According to Roy Glauber and Emilio Segrè, the original algorithm was invented by Enrico Fermi and reinvented by Stanislaw Ulam [6].

SA was independently described by Scott Kirkpatrick, C. Daniel Gelatt and Mario P. Vecchi in 1983 [7], at that time affiliated with IBM Thomas J. Watson Research Center, Yorktown Heights, and by Vlado Černý from Comenius University, Bratislava in 1985 [8].

Quotes

In the 2003 conference proceedings Celebrating the 50th Anniversary of the Metropolis Algorithm [9] [10], Marshall Rosenbluth describes the algorithm in the following beautifully concise and clear manner [11]: 

A simple way to do this [sampling configurations with the Boltzmann weight], as emerged after discussions with Teller, would be to make a trial move: if it decreased the energy of the system, allow it; if it increased the energy, allow it with probability exp(−ΔE/kT) as determined by a comparison with a random number. Each step, after an initial annealing period, is counted as a member of the ensemble, and the appropriate ensemble average of any quantity determined.

Applications

SA has multiple applications in discrete NP-hard optimization problems such as the Travelling salesman problem, in machine learning, in training of neural networks, and in the domain of computer games and computer chess in automated tuning as elaborated by Peter Mysliwietz in his Ph.D. thesis [12] to optimize the evaluation weight vector in Zugzwang. In its variant of temporal difference learning to adjust pattern weights in Morph, Robert Levinson at al. used simulated annealing as metaheuristic to set its own learning rate for each pattern, the more frequently a pattern is updated, the slower becomes its learning rate [13] [14] [15].

Algorithm

Description

The control flow of the algorithm is determined by two nested loops, the outer loop over decreasing temperature simulates the cooling, and an inner loop times n Monte Carlo iterations. Each time a randomly picked neighbor state inside the inner loop provides a better energy or fitness than the current state, the neighbor becomes the new current and even new optimum if fitter than fittest so far. Otherwise, if the neighbor fitness does not exceed current, it might still become current depending on the positive fitness or energy difference ΔE, and absolute temperature T, with a probability p according to the Boltzmann factor:

SimulatedAnnealingBoltzmannFactor.jpg

where k the Boltzmann constant, and e base of the exponential function whose negative exponent ensures the [0, 1] probability interval. Accepting worse solutions is a primary feature of SA, and important to stop greedy exploitation a local optimum but to explore other areas - higher temperatures favor exploration, while decreasing temperatures make the algorithm to behave greedier in favoring exploitation of the hopefully global optimum.

Animation

Hill Climbing with Simulated Annealing.gif

Simulated annealing - searching for a maximum. [16]
With the high temprature, the numerous local maxima are left quickly through the strong noise movement -
but the global maximum is reliably found because of cooling temperature is no longer sufficient to leave it.

Pseudo Code

The C like pseudo code is based on Peter Mysliwietz' description as given in his Ph.D. thesis [17]. Several neighbor functions used to modify the weight vector were tried, where one randomly chosen element changed randomly performed well. The fitness function inside the inner loop is of course the most time consuming part. For Zugzwang, Mysliwietz used a database of 500 test-positions with a search depth of one ply, which took about three minutes on a T 800 Transputer per iteration - the higher the hit rate of found expert moves, the fitter. The whole optimization used a tHight to tLow ratio of 100, a reduction factor r of 0.95, and n=40 inner iterations. 

/**
 * simulatedAnnealing
 * @author Peter Mysliwietz, slightly modified
 * @param tHigh is the start temperature
 * @param  tLow is the minimal end temperature
 * @param     r is the temperature reduction factor < 1.0   
 * @param     n number of iterations for each temperature     
 * @return best weight vector
 */
vector simulatedAnnealing(double tHigh, double tLow, double r, int n) {
   vector currentWeights = randomWeights();
   vector bestWeights = currentWeights;
   double fittest = fitness(currentWeights);

   for (double t = tHigh; t > tLow; t *= r) {
      for (int i = 0; i < n; ++i) {
         vector neighborWeights = neighbor(currentWeights);
         if ( fitness(neighborWeights ) > fitness(currentWeights) ) {
            currentWeights = neighborWeights;         
            if ( fitness(neighborWeights ) > fittest ) {
               fittest = fitness(neighborWeights);
               bestWeights = neighborWeights;
            }
         } else if (accept( fitness(currentWeights) - fitness(neighborWeights ), t) ) {
            currentWeights = neighborWeights;
         }
      } /* for i */
   } /* for t */
   return bestWeights;
}

/**
 * accept
 * @param d is the energy difference >= 0
 * @param t is the current temperature
 * @return true with probability of Boltzmann factor e^(-d/kt) 
 */
bool accept(double d, double t ) {
   const double k = 1.38064852e−23; /* joule / kelvin */
   double p = exp(-d / (k*t) ); 
   double r = rand() / (RAND_MAX + 1.0);
   return r < p;
}

[18] [19]

See also

Selected Publications

[20]

1948 ...

1950 ...

1970 ...

1980 ...

1990 ...

2000 ...

2010 ...

Forum Posts

External Links

Simulated Annealing

Related Topics

Misc

References

  1. ↑ train wheel production, Bochumer Verein, Bochum, Germany, ExtraSchicht 2010, The Industrial Heritage Trail, image by Rainer Halama, June 19, 2010, CC BY-SA 3.0, Wikimedia Commons, Glühen from Wikipedia.de (German)
  2. ↑ Saul B. Gelfand, Sanjoy K. Mitter (1985). Analysis of simulated annealing for optimization. 24th IEEE Conference on Decision and Control
  3. ↑ Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller, Edward Teller (1953). Equation of State Calculations by Fast Computing Machines. Journal of Chemical Physics, Vol. 21, No. 6
  4. ↑ Nicholas Metropolis (1987). The Beginning of the Monte Carlo Method. Los Alamos Science Special, pdf
  5. ↑ W. Keith Hastings (1970). Monte Carlo Sampling Methods Using Markov Chains and Their Applications. University of Toronto, Biometrika, Vol. 57, No. 1, pdf
  6. ↑ Metropolis–Hastings algorithm from Wikipedia
  7. ↑ Scott Kirkpatrick, C. Daniel Gelatt, Mario P. Vecchi (1983). Optimization by Simulated Annealing. Science, Vol. 220, No. 4598, pdf
  8. ↑ Vlado Černý (1985). Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. Journal of Optimization Theory and Applications, Vol. 45, No. 1
  9. ↑ The Monte Carlo Method in Physical Sciences: Celebrating the 50th Anniversary of the Metropolis Algorithm
  10. ↑ James Gubernatis (ed.) (2003). The Monte Carlo Method in Physical Sciences: Celebrating the 50th Anniversary of the Metropolis Algorithm. AIP Conference Proceedings
  11. ↑ James Gubernatis (2005). Marshall Rosenbluth and the Metropolis Algorithm. Physics of Plasmas, Vol. 12, No. 5, pdf
  12. ↑ Peter Mysliwietz (1994). Konstruktion und Optimierung von Bewertungsfunktionen beim Schach. Ph.D. thesis (German)
  13. ↑ Robert Levinson (1994). Experience-Based Creativity. Artificial Intelligence and Creativity: An Interdisciplinary Approach, Kluwer
  14. ↑ Ari Shapiro, Gil Fuchs, Robert Levinson (2002). Learning a Game Strategy Using Pattern-Weights and Self-play. CG 2002, pdf
  15. ↑ Johannes Fürnkranz (2000). Machine Learning in Games: A Survey. Austrian Research Institute for Artificial Intelligence, OEFAI-TR-2000-3, pdf
  16. ↑ Start temperature: 25 step: 0.1 End temperature: 0 - 1,000,000 iterations at each temperature: Animated GIF Hill Climbing with Simulated Annealing by Kingpin13, Wikimedia Commons, Simulated annealing from Wikipedia
  17. ↑ Peter Mysliwietz (1994). Konstruktion und Optimierung von Bewertungsfunktionen beim Schach. Ph.D. thesis, 7.4. Simulated Annealing, 7.4.2. Beschreibung des Algorithmus, Abb. 29, pp. 146 (German)
  18. ↑ Exponential function from Wikipedia
  19. ↑ C mathematical functions - Random number generation from Wikipedia
  20. ↑ Monte Carlo History by Dario Bressanini
  21. ↑ Schwellenakzeptanz from Wikipedia.de (German)
  22. ↑ The Monte Carlo Method in Physical Sciences: Celebrating the 50th Anniversary of the Metropolis Algorithm
  23. ↑ Vehicle routing problem from Wikipedia

Up one Level

Retrieved from "https://www.chessprogramming.org/index.php?title=Simulated_Annealing&oldid=20178"