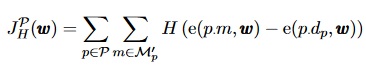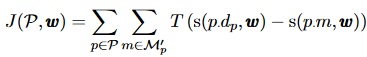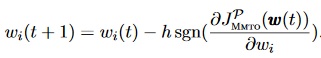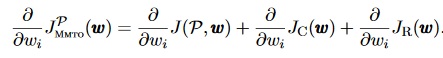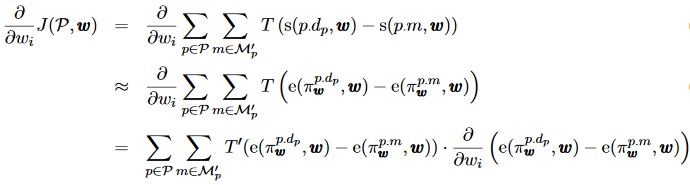Minimax Tree Optimization
Home * Automated Tuning * Minimax Tree Optimization
Minimax Tree Optimization (MMTO),
a supervised tuning method based on move adaptation,
devised and introduced by Kunihito Hoki and Tomoyuki Kaneko [2].
A MMTO predecessor, the initial Bonanza-Method was used in Hoki's Shogi engine Bonanza in 2006, winning the WCSC16 [3].
The further improved MMTO version of Bonanaza won the WCSC23 in 2013 [4].
Contents
Move Adaptation
A chess program has an linear evaluation function e(p,ω), where p is the game position and ω the feature weight vector to be adjusted for optimal play. The optimization procedure iterates over a set of selected positions from games assuming played by an oracle with a desired move given. All possible moves from this position are made and the resulting position evaluated. Each move obtaining a higher score than the desired move adds a penalty to the objective function to be minimized, for instance [5]:
Here, p.m is the position after move m in p, dp is the desired move in p, ℳ′p is the set of all legal moves in p excluding dp, and H(x) is the Heaviside step function. The numerical procedures to minimize such an objective function are complicated, and the adjustment of a large-scale vector ω seemed to present practical difficulties considering partial derivation and local versus global minima.
MMTO
MMTO improved by performing a minimax search (One or two ply plus quiescence), by grid-adjacent update, and using equality constraint and L1 regularization to achieve scalability and stability.
Objective Function
MMTO's objective function consists of the sum of three terms, where the first term J(P,ω) on the right side is the main part.
The other terms JC and JR are constraint and regularization terms. JC(P,ω) = λ0g(ω'), where ω' is subset of ω, g(ω')=0 is an equality constraint, and λ0 is a Lagrange multiplier. JR(P,ω) = λ1|ω''| is the L1 regularization. where λ1 is a constant > 0 and ω'' is subset of ω. The main part of objective function is similar to the H-formula of the Move Adaptation chapter:
where s(p,ω) is the value identified by the minimax search for position p. T(x) = 1/(1 + exp(ax)), a sigmoid function with slope controlled by a, to even become the Heaviside step function.
Optimization
The iterative optimization process has three steps:
- Perform a minimax search to identify PV leaves πω(t)p.m for all child positions p.m of position p in training set P, where ω(t) is the weight vector at the t-th iteration and ω(0) is the initial guess
- Calculate a partial-derivative approximation of the objective function using both πω(t)p.m and ω(t). The objective function employs a differentiable approximation of T(x), as well as a constraint and regularization term
- Obtain a new weight vector ω(t+1) from ω(t) by using a grid-adjacent update guided by the partial derivatives computed in step 2. Go back to step 1, or terminate the optimization when the objective function value converges
Because step 1 is the most time-consuming part, it is worth considering omitting it by assuming the PV does not change between iterations. In their experiments, Hoki and Kaneko used steps 2 and 3 32 times without running step 1.
Grid-Adjacent Update
MMTO uses grid-adjacent update to get ω(t+1) from ω(t) using a small integer h along with the sgn function of the partial derivative approximation.
Partial Derivative Approximation
In each iteration, feature weights are updated on the basis of the partial derivatives of the objective function.
The JR derivative is treated in an intuitive manner sgn(ωi)λ1 for ωi ∈ ω'', and 0 otherwise.
The partial derivative of the constraint term JC is 0 for ωi ∉ ω' . Otherwise, the Lagrange multiplier λ0 is set to the median of the partial derivatives in order to maintain the constraint g(ω) = 0 in each iteration. As a result, ∆ω′i is h for n feature weights, −h for n feature weights, and 0 in one feature weight, where the number of feature weights in ω' is 2n + 1.
Since the objective function with the minimax values s(p, ω) is not always differentiable, an approximation is used by using the evaluation of the PV leaf:
where T'(x) = d/dx T(x).
See also
Publications
- Kunihito Hoki (2006). Optimal control of minimax search result to learn positional evaluation. 11th Game Programming Workshop (Japanese)
- Tomoyuki Kaneko, Kunihito Hoki (2011). Analysis of Evaluation-Function Learning by Comparison of Sibling Nodes. Advances in Computer Games 13
- Kunihito Hoki, Tomoyuki Kaneko (2011). The Global Landscape of Objective Functions for the Optimization of Shogi Piece Values with a Game-Tree Search. Advances in Computer Games 13
- Kunihito Hoki, Tomoyuki Kaneko (2014). Large-Scale Optimization for Evaluation Functions with Minimax Search. JAIR Vol. 49, pdf
- Takenobu Takizawa, Takeshi Ito, Takuya Hiraoka, Kunihito Hoki (2015). Contemporary Computer Shogi. Encyclopedia of Computer Graphics and Games
Forum Posts
- MMTO for evaluation learning by Jon Dart, CCC, January 25, 2015
- Re: Texel tuning method question by Jon Dart, CCC, June 07, 2017
References
- ↑ Photo of the full cast of the television program Bonanza on the porch of the Ponderosa from 1962. From top: Lorne Greene, Dan Blocker, Michael Landon, Pernell Roberts. This episode, "Miracle Maker", aired in May 1962, Author: Pat MacDermott Company, Directional Public Relations, for Chevrolet, the sponsor of the program. During the 1950s and 1960s, publicity information was often distributed through ad or public relations agencies by the network, studio, or program's sponsor. In this case, the PR agency was making this available for Chevrolet--the little "plug" about their vehicles is seen in the release. Category:Bonanza (TV series) - Wikimedia Commons
- ↑ Kunihito Hoki, Tomoyuki Kaneko (2014). Large-Scale Optimization for Evaluation Functions with Minimax Search. JAIR Vol. 49, pdf
- ↑ Kunihito Hoki (2006). Optimal control of minimax search result to learn positional evaluation. 11th Game Programming Workshop (Japanese)
- ↑ Takenobu Takizawa, Takeshi Ito, Takuya Hiraoka, Kunihito Hoki (2015). Contemporary Computer Shogi. Encyclopedia of Computer Graphics and Games
- ↑ Description and Formulas based on Kunihito Hoki, Tomoyuki Kaneko (2014). Large-Scale Optimization for Evaluation Functions with Minimax Search. JAIR Vol. 49, pdf