General Setwise Operations
Home * Board Representation * Bitboards * General Setwise Operations
General Setwise Operations,
binary and unary operations, essential in testing and manipulating bitboards within a chess program. Relational operators on bitboards test for equality, bitwise boolean operators perform the intrinsic setwise operations [2] [3], such as intersection, union and complement. Shifting bitboards simulates piece movement, while finally arithmetical operations are used in bit-twiddling applications and to calculate various hash-indicies.
Operators are denoted with focus on the C, C++, Java and Pascal programming languages, as well as the mnemonics of x86 or x86-64 Assembly language instructions including bit-manipulation (BMI1, BMI2, TBM) and SIMD expansions (MMX, SSE2, AVX, AVX2, AVX-512, XOP), Mathematical symbols, some Venn diagrams [4], Truth tables, and bitboard diagrams where appropriate.
Contents
- 1 Relational
- 2 Bitwise Boolean
- 3 Shifting Bitboards
- 4 Arithmetic Operations
- 5 Selected Publications
- 6 Forum Posts
- 7 External Links
- 8 References
Relational
Relational operators on bitboards are the test for equality whether they are the same or not. Greater or less in the arithmetical sense is usually not relevant with bitboards [5] - instead we often compare bit for bit of two bitboards by certain bitwise boolean operations to retrieve bitwise greater, less or equal results.
Equality
In C, C++ or Java "==" is used, to test for equality, "!=" for not equal. Pascal uses "=", "<>" and has ":=" to distinguish relational equal operators from assignment.
if (a == b) -> both sets are equal if (a != b) -> both sets are not equal
x86-mnemonics
x86 has a cmp-instruction, which internally performs a subtraction to set its internal processor flags (carry, zero, overflow) accordantly, for instance the zero-flag if both sets are equal. Those flags are then used by conditional jump or move instructions.
cmp rax, rbx ; rax == rbx je equal ; (jz) conditional jump if equal (jne, jnz for not equal)
Empty and Universe
Two important sets are:
- The empty set is represented by all bits zero.
- The universal set contains all elements by setting all bits to binary one.
The numerical values and setwise representations of those sets:
empty set E = 0
set-wise = {}
universal set U = 2^64 - 1
signed decimal = -1
hexadecimal = 0xffffffffffffffff
unsigned decimal = 18,446,744,073,709,551,615
set-wise = {a1, b1, c1, d1, ....., e8, f8, g8, h8}
as bitboard diagrams and Venn diagrams
Empty Universe
. . . . . . . . 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1
Programmers often wonder to use -1 in C, C++ as unsigned constant. See The Two's Complement - alternately one may use ~0 to define the universal set. Since in C or C++, decimal numbers without ULL suffix are treated as 32-bit integers, constants outside the integer range need some care concerning sign or zero extension. Const declarations or using the C64 Macro is recommended:
const U64 universe = 0xffffffffffffffffULL;
To test whether a set is empty or not, one may compare with zero or use the logical not operator '!' in C, C++ or Java:
if (a == 0) -> empty set if (!a) -> empty set if (a != 0) -> set is not empty if (a) -> set is not empty
To test for the universal set is less likely:
if (a == universe) -> universal set if (a + 1 == 0) -> universal set
Bitwise Boolean
Boolean algebra is an algebraic structure [6] [7] that captures essential properties of both set operations and logical operations. The properties of associativity, commutativity, and absorption, which define an ordered lattice, in conjunction with distributive and complement laws define the Algebra of sets is in fact a Boolean algebra.
Specifically, Boolean algebra deals with the set operations of intersection, union and complement, their equivalents of conjunction, disjunction and negation and their bitwise boolean operations of AND, OR and NOT to implement combinatorial logic in software. Bitwise boolean operations on 64-bit words are in fact 64 parallel operations on each bit performing one setwise operation without any "side-effects". Square mapping don't cares as long all sets use the same.
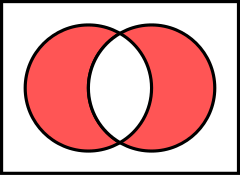
Intersection
In set theory intersection is denoted as:
A ∩ B
In boolean algebra conjunction is denoted as:
a ∧ b
Bitboard intersection or conjunction is performed by bitwise and (binary operator & in C, C++ or Java, and the keyword "AND" in Pascal).
intersection = a & b
Truth Table
Truth table of and for one bit, for a '1' result both inputs need to be '1':
| a | b | a and b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Conjunction acts like a bitwise minimum, min(a, b) or as bitwise multiplication (a * b).
x86-mnemonics
x86 has general purpose instruction as well as SIMD-instructions for bitwise and:
and rax, rbx ; rax &= rbx test rax, rbx ; to determine whether the intersection is empty pand mm0, mm1 ; MMX mm0 &= mm1 pand xmm0, xmm1 ; SSE2 xmm0 &= xmm1 vpand xmm0, xmm1, xmm2 ; AVX xmm0 = xmm1 & xmm2 vpand ymm0, ymm1, ymm2 ; AVX2 ymm0 = ymm1 & ymm2
SSE2-intrinsic _mm_and_si128
AVX2-intrinsic _mm256_and_si256
AVX-512 has VPTERNLOG
Idempotent
Conjunction is idempotent.
a & a == a
Commutative
Conjunction is commutative
a & b == b & a
Associative
Conjunction is associative.
(a & b) & c == a & (b & c)
Subset
The intersection of two sets is subset of both.
Assume we have a attack set of a queen, and like to know whether the queen attacks opponent pieces it may capture, we need to 'and' the queen-attacks with the set of opponent pieces.
queen attacks & opponent pieces = attacked pieces . . . . . . . . 1 . . 1 1 . . 1 . . . . . . . . . . . 1 . . 1 . 1 . 1 1 1 1 1 . . . . 1 . . 1 . . 1 . 1 . 1 . . . 1 . . . . . 1 . 1 . . . . . . . . 1 1 1 . . . . . . . . . . . . . . . . . . . 1 1 1 * 1 1 1 . & . . . * . . 1 . = . . . * . . 1 . . . 1 1 1 . . . . . . . . . . . . . . . . . . . . . . 1 . 1 . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . . . . .
To prove whether set 'a' is subset of another set 'b', we compare whether the intersection equals the subset:
bool isASubsetOfB(U64 a, U64 b) {return (a & b) == a;}
Disjoint Sets
To test whether two sets are disjoint - that is their intersection is empty - compiler emit the x86 test-instruction instead of and. That saves the content of a register, if the intersection is not otherwise needed:
if ( (a & b) == 0 ) -> a and b are disjoint sets
In chess the bitboards of white and black pieces are obviously always disjoint, same for sets of different piece-types, such as knights or pawns. Of course this is because one square is occupied by one piece only.
Union
In set theory union is denoted as:
A ∪ B
In boolean algebra disjunction is denoted as:
a ∨ b
The union or disjunction of two bitboards is applied by bitwise or (binary operator | in C, C++ or Java, or the keyword "OR" in Pascal). The union is superset of the intersection, while the intersection is subset of the union.
union = a | b
Truth Table
Truth table of or for one bit, one set input bits is sufficient to set the output:
| a | b | a or b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Disjunction acts like bitwise maximum, max(a, b) or as addition with saturation, min(a + b, 1). It can also be interpreted as sum minus product, a + b - a*b, with possible temporary overflow of one binary digit to two - or with modulo 2 arithmetic.
x86-mnemonics
x86 has general purpose instruction as well as SIMD-instructions for bitwise or:
or rax, rbx ; rax |= rbx por mm0, mm1 ; MMX mm0 |= mm1 por xmm0, xmm1 ; SSE2 xmm0 |= xmm1 vpor xmm0, xmm1, xmm2 ; AVX xmm0 = xmm1 | xmm2 vpor ymm0, ymm1, ymm2 ; AVX2 ymm0 = ymm1 | ymm2
SSE2-intrinsic _mm_or_si128
AVX2-intrinsic _mm256_or_si256
AVX-512 has VPTERNLOG
Idempotent
Disjunction is idempotent.
a | a == a
Commutative
Disjunction is commutative
a | b == b | a
Associative
Disjunction is associative.
(a | b) | c == a | (b | c)
Distributive
Disjunction is distributive over conjunction and vice versa:
x | (y & z) == (x | y) & (x | z) x & (y | z) == (x & y) | (x & z)
Superset
The union of two sets is superset of both. For instance the union of all white and black pieces are the set of all occupied squares:
white pieces | black pieces = occupied squares . . . . . . . . 1 . 1 1 1 1 1 1 1 . 1 1 1 1 1 1 . . . . . . . . 1 1 1 1 . 1 1 1 1 1 1 1 . 1 1 1 . . . . . . . . . . 1 . . . . . . . 1 . . . . . . . . . . . . . . . . . 1 . . . . . . . 1 . . . . . . . 1 . . . | . . . . . . . . = . . . . 1 . . . . . . . . 1 . . . . . . . . . . . . . . . 1 . . 1 1 1 1 . 1 1 1 . . . . . . . . 1 1 1 1 . 1 1 1 1 1 1 1 1 1 . 1 . . . . . . . . 1 1 1 1 1 1 . 1
Since white and black pieces are always disjoint, one may use addition here as well. That fails for union of attack sets, since squares may be attacked or defended by multiple pieces of course.
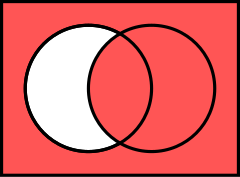
Complement Set
In set theory complement set is denoted as:
A∁
In boolean algebra negation is denoted as:
¬a
The complement set (absolute complement set), negation or ones' complement has it's equivalent in bitwise not (unary operator '~' in C, C++ or Java, or the keyword "NOT" in Pascal).
Truth Table
Truth table of not for one bit:
| a | not a |
|---|---|
| 0 | 1 |
| 1 | 0 |
The complement can be interpreted as bitwise subtraction (1 - a).
x86-mnemonics
Available as general purpose instruction.
not rax ; rax = ~rax
Empty Squares
The set of empty squares for instance is the complement-set of all occupied squares and vice versa:
~occupied squares = empty squares 1 . 1 1 1 1 1 1 . 1 . . . . . . 1 1 1 1 . 1 1 1 . . . . 1 . . . . . 1 . . . . . 1 1 . 1 1 1 1 1 . . . . 1 . . . 1 1 1 1 . 1 1 1 ~ . . . . 1 . . . = 1 1 1 1 . 1 1 1 . . . . . 1 . . 1 1 1 1 1 . 1 1 1 1 1 1 . 1 1 1 . . . . 1 . . . 1 1 1 1 1 1 . 1 . . . . . . 1 .
Don't confuse bitwise not with logical not-operator '!' in C:
!0 == 1 !(anything != 0) == 0 !1 == 0 !-1 == 0
Complement laws
- The union of a set with it's complement is the universal set -1.
- The intersection of a set with it's complement is the empty set 0 - both are disjoint.
- Empty set and universal set are complement sets.
a | ~a == -1 a & ~a == 0 ~0 == -1 ~(-1) == 0
De Morgan's laws
- Complement of union (NOR ) is the intersection of the complements [8].
- Complement of intersection (NAND or Sheffer stroke ) is the union of the complements.
~(a | b) == ~a & ~b ~(a & b) == ~a | ~b
For instance to get the set of empty squares, we can complement the union of white and black pieces. Or we can intersect the complements of white and black pieces.
Relative Complement
In set theory relative complement is denoted as:
A∁ ∩ B = B \ A
The relative complement is the absolute complement restricted to some other set. The relative complement of 'a' inside 'b' is also known as the set theoretic difference of 'b' minus 'a'. It is the set of all elements that belong to 'b' but not to 'a'. Also called 'b' without 'a'. It is the intersection of 'b' with the absolute complement of 'a'.
not_a_in_b = ~a & b b_without_a = b & ~a
Truth Table
Truth table of relative complement for one bit:
| a | b | b andnot a |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
The relative complement of 'a' in 'b' may be interpreted as a bitwise (a < b) relation.
x86-mnemonics
x86 don't has an own general purpose instruction for relative complement, but x86-64 expansion BMI1, and SIMD-instructions:
andn rax, rbx, rcx ; BMI1 rax = ~rbx & rcx pandn mm0, mm1 ; MMX mm0 = ~mm0 & mm1 pandn xmm0, xmm1 ; SSE2 xmm0 = ~xmm0 & xmm1 vpandn xmm0, xmm1, xmm2 ; AVX xmm0 = ~xmm1 & xmm2 vpandn ymm0, ymm1, ymm2 ; AVX xmm0 = ~xmm1 & xmm2
SSE2-intrinsic _mm_andnot_si128
AVX2-intrinsic _mm256_andnot_si256
AVX-512 has VPTERNLOG
Super minus Sub
In presumption of subtraction or exclusive or there are alternatives to calculate the relative complement - superset minus subset. We can take either the union without the complementing set - or the other set without the intersection
~a & b == ( a | b ) - a ~a & b == b - ( a & b )
Implication
Logical Implication or Entailment is denoted as:
A ⇒ B
The boolean Material conditional is denoted as:
a → b
Logical Implication or the boolean Material conditional 'a' implies 'b' (if 'a' then 'b') is an derived boolean operation, implemented as union of the absolute complement of 'a' with 'b':
a_implies_b == ~a | b
Truth Table Truth table of logical implication for one bit:
| a | b | a implies b |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Implication may be interpreted as a bitwise (a <= b) relation.
x86-mnemonics
AVX-512 has VPTERNLOG
Exclusive Or
In set theory symmetric difference is denoted as:
A ∆ B
In boolean algebra Exclusive or is denoted as:
a ⊕ b
Exclusive or, also exclusive disjunction (xor, binary operator '^' in C, C++ or Java, or the keyword "XOR" in Pascal),
xor = a ^ b
also called symmetric difference, leaves all elements which are exclusively set in one of the two sets. Xor is really a multi purpose operation with a lot of applications not only bitboards of course.
1 . . . . . . 1 . . . . . . . . 1 . . . . . . 1 . 1 . . . . 1 . . . . . . . . . . 1 . . . . 1 . . . 1 . . 1 . . . . 1 1 1 1 . . . . . 1 1 . . . . . . 1 1 . . . . . 1 1 1 1 . . . . 1 . . 1 . . . . . 1 1 . . . ^ . . 1 1 1 1 . . = . . 1 . . 1 . . . . 1 . . 1 . . . . 1 1 1 1 . . . . . 1 1 . . . . 1 . . . . 1 . . . . . . . . . . 1 . . . . 1 . 1 . . . . . . 1 . . . . . . . . 1 . . . . . . 1
Truth Table
Truth table of exclusive or for one bit:
| a | b | a xor b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Xor implements a bitwise (a != b) relation. It acts like a bitwise addition (modulo 2), since (1 + 1) mod 2 = 0. It also acts like a bitwise subtraction (modulo 2).
x86-mnemonics
x86 has general purpose instruction as well as SIMD-instructions for bitwise exclusive or:
xor rax, rbx ; rax ^= rbx pxor mm0, mm1 ; MMX mm0 ^= mm1 pxor xmm0, xmm1 ; SSE2 xmm0 ^= xmm1 vpxor xmm0, xmm1, xmm2 ; AVX xmm0 = xmm1 ^ xmm2 vpxor ymm0, ymm1, ymm2 ; AVX2 ymm0 = ymm1 ^ ymm2
SSE2-intrinsic _mm_xor_si128
AVX2-intrinsic _mm256_xor_si256
AVX-512 has VPTERNLOG
Commutative
Exclusive disjunction is commutative
a ^ b == b ^ a
Associative
Xor is associative as well.
(a ^ b) ^ c == a ^ (b ^ c)
Distributive
Conjunction is distributive over exclusive disjunction - but not vice versa, since conjunction acts like multiplication, while xor acts as addition in the Galois field GF(2) :
x & (y ^ z) == (x & y) ^ (x & z)
Own Inverse
If applied two (even) times with the same operand, xor restores the original result. It is own inverse or an involution .
Subset
If one operand is subset of the other, xor (or subtraction) implements the relative complement.
super sub super &~ sub . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 . . . . . . . . . . 1 1 1 1 1 1 . . 1 1 1 1 1 1 . . . 1 1 1 1 . . . 1 . . . . 1 . . 1 1 1 1 1 1 . ^ . . 1 1 1 1 . . . 1 . . . . 1 . . 1 1 1 1 1 1 . . . 1 1 1 1 . . = . 1 . . . . 1 . . 1 1 1 1 1 1 . - . . 1 1 1 1 . . . 1 . . . . 1 . . 1 1 1 1 1 1 . . . . . . . . . . 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . . . . .
Subtraction
While commutative, xor is a better replacement for subtracting from power of two minus one values, such as 63.
(2n - 1) - a == a ^ (2n - 1) with a subset of 2n - 1
This is because it usually safes one x86 load instruction and an additional register, but uses opcodes with immediate operands - for instance:
1 - a == a ^ 1 3 - a == a ^ 3 7 - a == a ^ 7 15 - a == a ^ 15 31 - a == a ^ 31 63 - a == a ^ 63 ... -1 - a == a ^ -1
Or without And
Xor is the same as a union without the intersection - all the bits different, 0,1 or 1,0. Since the intersection is subset of the union, xor or subtraction can replace the "without" operation & ~:
a ^ b == (a | b) &~(a & b) a ^ b == (a | b) ^ (a & b) a ^ b == (a | b) - (a & b)
Disjoint Sets
The symmetric difference of disjoint sets is equal to the union or arithmetical addition. Since intersection and symmetric difference are disjoint, the union might defined that way:
a | b = ( a & b ) ^ ( a ^ b ) a | b = ( a & b ) ^ a ^ b a | b = ( a & b ) | ( a ^ b ) a | b = ( a & b ) + ( a ^ b )
Assume we have distinct attack sets of pawns in left or right direction. The set of all squares attacked by two pawns is the intersection, the set exclusively attacked by one pawn (either right or left) is the xor-sum, while all squares attacked by any pawn is the union, see pawn attacks.
Union of Complements
The symmetric difference is equivalent to the union of both relative complements. Since both relative complements are disjoint, bitwise or or add can replaced by xor itself:
a ^ b == (a & ~b) | (b & ~a) a ^ b == (a & ~b) ^ (b & ~a) a ^ b == (a & ~b) + (b & ~a)
Toggle
Xor can be used to toggle or flip bits by a mask.
x ^= mask;
Complement
xor with the universal set -1 flips each bit and results in the ones' complement.
a ^ -1 == ~a
Without
Due to distributive law and since symmetric difference of set and subset is the relative complement of subset in set, there are some equivalent ways to calculate the relative complement by xor. Based on surrounding expressions or whether subexpressions such as union, intersection or symmetric difference may be reused one may prefer the one or other alternative.
a & ~b == a & (-1 ^ b ) a & ~b == a & ( a ^ b ) a & ~b == a ^ ( a & b ) == a - ( a & b ) a & ~b == b ^ ( a | b ) == ( a | b ) - b
Also note that
a & a == a & -1
Clear
Since 'a' xor 'a' is zero, it is the shorter opcode to clear a register, since it takes no immediate operand. Applied by optimizing compilers. Same is true for subtraction by the way.
xor rax, rax ; same as mov rax, 0 pxor mm0, mm0 ; MMX 64-bit register pxor xmm0, xmm0 ; SSE2 - 128-bit xmm-register
Xor Swap
Three xors on the same registers swap their content: (Note: this only works when a and b are stored on distinct memory adresses!)
a ^= b b ^= a a ^= b
If we provide an intersection by a mask, ...
a = (a ^ b) & mask b ^= a a ^= b
... 'a' becomes 'b', but only a part of 'b', where mask is one, becomes 'a'.
Bits from two Sources
Getting arbitrary, disjoint bits from two sources by a mask:
// if mask-bit is zero, bit from a, otherwise from b - since a^(a^b) == b U64 mask = C64(0xFFFF0000FFFF0000); U64 result = a ^ ((a ^ b) & mask);
This takes one instruction less, than the union of relative complement of the mask in 'a' with intersection of mask with 'b'.
a ^ ((a ^ b) & mask)
== (a & ~mask) | (b & mask)
== (a & ~mask) ^ (b & mask) because both sets of the union are disjoint
== (a & ~mask) + (b & mask) because both sets of the union are disjoint
XOR-applications and affairs
- Calculation of hash-keys based on Zobrist-keys.
- Cyclic redundancy check, Parity words or Gray Code
- Fredkin gate by Edward Fredkin
- Hyperbola Quintessence.
- o^(o-2r).
- Robert Hyatt's approach of a lockless transposition table
- Swapping Bits.
- The XOR affair from Perceptrons by Marvin Minsky and Seymour Papert [9]
Equivalence
If and only if (Iff) is denoted as:
A ⇔ B
Logical equivalence is denoted as:
a ↔ b
Logical equality, logical equivalence or biconditional (if and only if, XNOR ) is the complement of xor.
a_equal_b == ~(a ^ b) a_equal_b == (a & b) | (~a & ~b) a_equal_b == (a & b) | ~(a | b)
Truth Table
Truth table of equivalence or for one bit:
| a | b | a ↔ b |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Equivalence implements a bitwise (a == b) relation.
x86-mnemonics
AVX-512 has VPTERNLOG
Majority
The majority function or median operator is a function from n inputs to one output. The value of the operation is false when n/2 or fewer arguments are false, and true otherwise. For two inputs it is the intersection. Three inputs require some more computation:
Truth Table
Truth table of majority for three inputs:
| a | b | c | maj(a,b,c) | 0 | 0 | 0 | 0 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | ||||
| 0 | 1 | 0 | 0 | ||||
| 0 | 1 | 1 | 1 | ||||
| 1 | 0 | 0 | 0 | ||||
| 1 | 0 | 1 | 1 | ||||
| 1 | 1 | 0 | 1 | ||||
| 1 | 1 | 1 | 1 |
major(a,b,c) = (a & b) | (a & c) | (b & c); major(a,b,c) = (a & b) | ((a ^ b ) & c);
See the application of cardinality of multiple sets for more than three inputs.
x86-mnemonics
AVX-512 VPTERNLOG imm8 = 0xe8 implements the majority function.
Greater One Sets
Greater One is a function from n inputs to one output. The value of the operation is true if more than one argument is true, false otherwise. Obviously, for two inputs it is the intersection, for three inputs it is the majority function. For more inputs it is the union of all distinct pairwise intersections, which can be expressed with setwise operators that way:
∪i>j∈I(Ai ∩ Aj)
With four bitboards this is equivalent to:
(a1 & a0) | (a2 & a1) | (a2 & a0) | (a3 & a2) | (a3 & a1) | (a3 & a0)
with
n * (n - 1) - 1
operations - that is 11 for n == 4.
O(n^2) to O(n)
Due to distibutive law one can factor out common sets ...
(a1 & ( a0)) | (a2 & ( a1|a0)) | (a3 & (a2|a1|a0))
... with further reductions of the number of operations, also due to aggregation of the inner or-terms. Three additional operations for an increment of n, thus the former quadratic increase becomes linear.
In general, as mentioned,
∪i>j∈I(Ai ∩ Aj)
requires
n * (n - 1) - 1
operations, which can be reduced to
3 * (n - 1) - 2
operations.
This O(n^2) to O(n) simplification is helpful to determine for instance knight fork target squares from eight distinct knight-wise direction attack sets of potential targets, like king, queen, rooks and hanging bishops or even pawns - or any other form of at least double attacks from n attack bitboards:
U64 attack[n]; // 0..n-1
U64 atLeastDouble = 0;
U64 atLeastSingle = a[0];
for (i=1; i < n; i++) {
atLeastDouble |= attack[i] & atLeastSingle;
atLeastSingle |= attack[i];
}
Well, if you need additionally at least triple attacks, you'll get the idea how this would work as well, see also Odd and Major Digit Counts from the Population Count page.
Shifting Bitboards
In the 8*8 board centric world with one scalar square-coordinate 0..63, each of the max eight neighboring squares can be determined by adding an offset for each direction. For border squares one has to care about overflows and wraps from a-file to h-file or vice versa. Some conditional code is needed to avoid that. Such code is usually part of move generation for particular pieces.
northwest north northeast
noWe nort noEa
+7 +8 +9
\ | /
west -1 <- 0 -> +1 east
/ | \
-9 -8 -7
soWe sout soEa
southwest south southeast
| Code samples and bitboard diagrams rely on Little endian file and rank mapping. |
In the setwise world of bitboards, where a square as member of a set is determined by an appropriate one-bit 2^square, the operation to apply such movements is shifting . Unfortunately most architectures don't support a "generalized" shift by signed values but only shift left or shift right. That makes bitboard code less general as one has usually separate code for each direction or at least for the positive and negative directions.
- Shift left (<<) is arithmetically a multiplication by power of two.
- Shift right (>> or >>> in Java [10]) is arithmetically a division by power of two.
Since the square-index is encoded as power of two exponent inside a bitboard, the power of two multiplication or division is adding or subtracting the square-index.
The reason the bitboard type-definintion is unsigned in C, C++ is to avoid so called arithmetical shift right in opposition to logical shift right . Arithmetical shift right implies filling one-bits in from MSB-direction if the operand is negative and has MSB bit 63 set. Logical shift right always shifts in zeros - that is what we need. Java has no unsigned types, but a special unsigned shift right operator >>>.
x86-mnemonics
x86 has general purpose instructions, BMI2 general purpose instructions not affecting processor flags, as well as SIMD-instructions for various shifts:
shr rax, cl ; rax >>= cl shl rax, cl ; rax <<= cl shrx r64a, r/m64, r64b; BMI2 r64a = r/m64 >> r64b shlx r64a, r/m64, r64b; BMI2 r64a = r/m64 << r64b psrlq mm0, mm1 ; MMX mm0 >>= mm1 psllq mm0, mm1 ; MMX mm0 <<= mm1 psrlq xmm0, xmm1 ; SSE2 xmm0 >>= xmm1 psllq xmm0, xmm1 ; SSE2 xmm0 <<= xmm1 vpsrlvq ymm0, ymm1, ymm2 ; AVX2 ymm0 = ymm1 >> ymm2 ; Individual shifts vpsllvq ymm0, ymm1, ymm2 ; AVX2 ymm0 = ymm1 << ymm2 ; Individual shifts
SSE2-intrinsics with variable register or constant immediate shift amounts, working on vectors of two bitboards:
AVX2 has individual shifts for each of four bitboards:
One Step Only
The advantage with bitboards is, that the shift applies to all set bits in parallel, e.g. with all pawns. Vertical shifts by +-8 don't need any under- or overflow conditions since bits simply fall out and disappear.
U64 soutOne (U64 b) {return b >> 8;}
U64 nortOne (U64 b) {return b << 8;}
Wraps from a-file to h-file or vice versa may be considered by only shifting subsets which may not wrap. Thus we can mask off the a- or h-file before or after a +-1,7,9 shift:
const U64 notAFile = 0xfefefefefefefefe; // ~0x0101010101010101 const U64 notHFile = 0x7f7f7f7f7f7f7f7f; // ~0x8080808080808080
Post-shift masks, ...
U64 eastOne (U64 b) {return (b << 1) & notAFile;}
U64 noEaOne (U64 b) {return (b << 9) & notAFile;}
U64 soEaOne (U64 b) {return (b >> 7) & notAFile;}
U64 westOne (U64 b) {return (b >> 1) & notHFile;}
U64 soWeOne (U64 b) {return (b >> 9) & notHFile;}
U64 noWeOne (U64 b) {return (b << 7) & notHFile;}
... and pre-shift, with the mirrored file masks.
U64 eastOne (U64 b) {return (b & notHFile) << 1;}
U64 noEaOne (U64 b) {return (b & notHFile) << 9;}
U64 soEaOne (U64 b) {return (b & notHFile) >> 7;}
U64 westOne (U64 b) {return (b & notAFile) >> 1;}
U64 soWeOne (U64 b) {return (b & notAFile) >> 9;}
U64 noWeOne (U64 b) {return (b & notAFile) << 7;}
SSE2 one step only provides some optimizations according to the wraps on vectors of two bitboards.
Main application of shifts is to get attack sets or move-target sets of appropriate pieces, eg. one step for pawns and king. Applying one step multiple times may used to generate attack sets and moves of pieces like knights and sliding pieces.
For instance all push-targets of white pawns can be determined with one shift left plus intersection with empty squares.
whiteSinglePawnPushTargets = nortOne(whitePawns) & emptySquares;
Square-Mapping is crucial while shifting bitboards. Shifting left inside a computer word may mean shifting right on the board with little-endian file-mapping as used in most sample code here.
Rotate
For the sake of completeness - Rotate is similar to shift but wraps bits around. Rotate does not alter the number of set bits. With x86-64 like shift operand s modulo 64, each bit index i, in the 0 to 63 range, is transposed by
rotateLeft ::= i := (i + s) mod 64 rotateRight::= i := (i - s) mod 64
Additionally, following relations hold:
rotateLeft (s) == rotateRight(64-s) rotateRight(s) == rotateLeft (64-s)
Most processors have rotate instructions, but are not supported by standard programming languages like C or Java. Some compilers provide intrinsic, processor specific functions.
U64 rotateLeft (U64 x, int s) {return _rotl64(x, s);}
U64 rotateRight(U64 x, int s) {return _rotr64(x, s);}
x86-mnemonics
rol rax, cl ror rax, cl
Rotate by Shift
Otherwise rotate has to be emulated by shifts, with some chance optimizing compiler will emit exactly one rotate instruction.
U64 rotateLeft (U64 x, int s) {return (x << s) | (x >> (64-s));}
U64 rotateRight(U64 x, int s) {return (x >> s) | (x << (64-s));}
Since x86-64 64-bit shifts are implicitly modulo 64 (and 63), one may replace (64-s) by -s.
Generalized Shift
shifts left for positive amounts, but right for negative amounts.
U64 genShift(U64 x, int s) {
return (s > 0) ? (x << s) : (x >> -s);
}
If compiler are not able to produce speculative execution of both shifts with a conditional move instruction, one may try an explicit branch-less solution:
/**
* generalized shift
* @author Gerd Isenberg
* @param x any bitboard
* @param s shift amount -64 < s < +64
* left if positive
* right if negative
* @return shifted bitboard
*/
U64 genShift(U64 x, int s) {
char left = (char) s;
char right = -((char)(s >> 8) & left);
return (x >> right) << (right + left);
}
Due to the value range of the shift, one may save the arithmetical shift right in assembly:
; input ; ecx - shift amount, ; left if positive ; right if negative ; rax - bitboard to shift mov dl, cl and cl, ch neg cl shr rax, cl add cl, dl shl rax, cl
One Step
x86-64 rot64 works like a generalized shift with positive or negative shift amount - since it internally applies an unsigned modulo 64 ( & 63) and makes -i = 64-i. We need to clear either the lower or upper bits by intersection with a mask, which might be combined with the wrap-ands for one step. It might be applied to get attacks for both sides with a direction parameter and small lookups for shift amount and wrap-ands - instead of multiple code for eight directions. Of course generalized shift will be a bit slower due to lookups and using cl as the shift amount register.
// positve left, negative right shifts
int shift[8] = {9, 1,-7,-8,-9,-1, 7, 8};
U64 avoidWrap[8] =
{
0xfefefefefefefe00,
0xfefefefefefefefe,
0x00fefefefefefefe,
0x00ffffffffffffff,
0x007f7f7f7f7f7f7f,
0x7f7f7f7f7f7f7f7f,
0x7f7f7f7f7f7f7f00,
0xffffffffffffff00,
};
U64 shiftOne (U64 b, int dir8) {
return _rotl64(b, shift[dir8]) & avoidWrap[dir8];
}
The avoidWrap masks by some arbitrary dir8 enumeration and shift amount:
6 == noWe -> +7 7 == nort -> +8 0 == noEa -> +9 0x7F7F7F7F7F7F7F00 0xFFFFFFFFFFFFFF00 0xFEFEFEFEFEFEFE00 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . . . . 5 == west -> -1 1 == east -> +1 0x7F7F7F7F7F7F7F7F 0xFEFEFEFEFEFEFEFE 1 1 1 1 1 1 1 . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . . 1 1 1 1 1 1 1 4 == soWe -> -9 3 == sout -> -8 2 == soEa -> -7 0x007F7F7F7F7F7F7F 0x00FFFFFFFFFFFFFF 0x00FEFEFEFEFEFEFE . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1
See also
Bit by Square
Since single populated bitboards are always power of two values, shifting 2^0 left implements pow2(square) to convert square-indices to a member of a bitboard.
U64 singleBitset = C64(1) << square; // or lookup[square]
The inverse function square = log2(x), is topic of bitscan and bitboard serialization.
Shift versus Lookup
While 1 << square sounds cheap, it is rather expensive in 32-bit mode - and therefor often precalculated in a small lookup-table of 64-single bit bitboards. Also, on x86-64-processors a variable shift is restricted to the byte-register cl. Thus, two or more variable shifts are constrained by sequential execution [11].
Test
Test a bit of a square-index by intersection-operator 'and'.
if (x & singleBitset) -> bit is set;
Set
Set a bit of a square-index by union-operator 'or'.
x |= singleBitset; // set bit
Toggle
Toggle a bit of square-index by xor.
x ^= singleBitset; // toggle bit
Reset
Reset a bit of square-index by relative complement of the single bit,
x &= ~singleBitset; // reset bit
or conditional toggle by single bit intersection
x ^= singleBitset & x; // reset bit
Set and toggle (or, xor) might the faster way to reset a bit inside a register (not, and).
x |= singleBitset; // set bit x ^= singleBitset; // resets set bit
If singleBitset needs to preserved, an extra register is needed for the complement.
x86-Instructions
x86 processor provides a bit-test instruction family (bt, bts, btr, btc) with 32- and 64-bit operands. They may be used implicitly by compiler optimization or explicitly by inline assembler or compiler intrinsics. Take care that they are applied on local variables likely registers rather than memory references [12]:
Update by Move
This technique to toggle bits by square is likely used to initialize or update the bitboard board-definition. While making or unmaking moves, the single bit either correspondents with the from- or to-square of the move. Which particular bitboard has to be updated depends on the moving piece or captured piece.
For simplicity we assume piece plus color and captured piece are member or method of a move-structure/class.
Quiet moves toggle both from- and to-squares of the piece-bitboard, as well for the redundant union-sets:
U64 fromBB = C64(1) << move->from; U64 toBB = C64(1) << move->to; U64 fromToBB = fromBB ^ toBB; // |+ pieceBB[move->piece] ^= fromToBB; // update piece bitboard pieceBB[move->color] ^= fromToBB; // update white or black color bitboard occupiedBB ^= fromToBB; // update occupied ... emptyBB ^= fromToBB; // ... and empty bitboard
Captures need to consider the captured piece of course:
U64 fromBB = C64(1) << move->from; U64 toBB = C64(1) << move->to; U64 fromToBB = fromBB ^ toBB; // |+ pieceBB[move->piece] ^= fromToBB; // update piece bitboard pieceBB[move->color] ^= fromToBB; // update white or black color bitboard pieceBB[move->cPiece] ^= toBB; // reset the captured piece pieceBB[move->cColor] ^= toBB; // update color bitboard by captured piece occupiedBB ^= fromBB; // update occupied, only from becomes empty emptyBB ^= fromBB; // update empty bitboard
Similar for special moves like castling, promotions and en passant captures.
Upper Squares
To get a set of all upper squares or bits, either shift ~1 or -2 left by square:
U64 upperBits = C64(~1) << sq;
for instance d4 (27)
high = ~1 << d4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . . . . 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . . . .
Lower Squares
Lower squares are simply Bit by Square minus one.
U64 lowerBits = (C64(1 ) << sq) - 1);
for instance d4 (27)
low = (1<<d4)-1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Swapping Bits
Swapping none overlapping bit-sequences in a bitboard is the base of a lot of permutation tricks.
by Position
Suppose we like to swap n bits from two none overlapping bit locations of a bitboard. The trick is to set all n least significant bits by subtracting one from n power of 2. Both substrings are shifted to bit zero, exclusive ored and masked by the n ones. This sequence is then twice shifted back to their original places, while the union (xor-union due to disjoint bits) is finally exclusive ored with the original bitboard to swap both sequences.
/**
* swap n none overlapping bits of bit-index i with j
* @param b any bitboard
* @param i,j positions of bit sequences to swap
* @param n number of consecutive bits to swap
* @return bitboard b with swapped bit-sequences
*/
U64 swapNBits(U64 b, int i, int j, int n) {
U64 m = ( 1 << n) - 1;
U64 x = ((b >> i) ^ (b >> j)) & m;
return b ^ (x << i) ^ (x << j);
}
For instance swap 6 bits each, from bit-index 9 (bits named ABCDEF, either 0,1) with bit-index 41 (abcdef):
b m = (1<<6) - 1 . . . . . . . . . . . . . . . . * . . . . . . . . . . . . . . . *|a b c d e f|* . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . *|A B C D E F|* . . . . . . . . . . . . . . . . 1 1 1 1 1 1 . . b >> j ^ b >> i => x = .xor & m with . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . r = a ^ A . . . . . . . . a b c d e f * * . . . . . . . . s = b ^ B . . . . . . . . ^ . . . . . . . * => . . . . . . . . t = c ^ C . . . . . . . . . . . . . . . . . . . . . . . . u = d ^ D . . . . . . . . . . . . . . . . . . . . . . . . v = e ^ E a b c d e f * * A B C D E F * . r s t u v w . . w = f ^ F b ^ x << i | x << j => swapNBits(9,41,6) . . . . . . . . . . . . . . . . . . . . . . . . * . . . . . . . . . . . . . . . * . . . . . . . *|a b c d e f|* . r s t u v w . *|A B C D E F|* . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ^ . . . . . . . . => . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . *|A B C D E F|* . r s t u v w . *|a b c d e f|* . . . . . . . . . . . . . . . . . . . . . . . .
Delta Swap
To swap any none overlapping pairs we can shift by the difference (j-i, with j>i) and supply an explicit mask with a '1' on the least significant position for each pair supposed to be swapped.
/**
* swap any none overlapping pairs of bits
* that are delta places apart
* @param b any bitboard
* @param mask has a 1 on the least significant position
* for each pair supposed to be swapped
* @param delta of pairwise swapped bits
* @return bitboard b with bits swapped
*/
U64 deltaSwap(U64 b, U64 mask, int delta) {
U64 x = (b ^ (b >> delta)) & mask;
return x ^ (x << delta) ^ b;
}
To apply the swapping of the swapNBits sample above, we call deltaSwap with delta of 32 and 0x7E00 as mask. But we may apply any arbitrary and often periodic mask pattern, as long as no overlapping occurs. The intersection of mask with (mask << delta) must therefor be empty. But we can also swap odd or even files of a bitboard by calling deltaSwap with delta of one, and mask of 0x5555555555555555:
1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 . 1 .
Applications of delta swaps are flipping, mirroring and rotating. In Knuth's The Art of Computer Programming, Vol 4, page 13, bit permutation in general [13], he mentions 2^k delta swaps with k = {0,1,2,3,4,5,4,3,2,1,0} to obtain any arbitrary permutation. Special cases might be cheaper.
Arithmetic Operations
At the first glance, arithmetic operations, that is addition, subtraction, multiplication and division, doesn't make much sense with bitboards. Still, there are some bit-twiddling applications related to least significant one bit (LS1B), to enumerate all subsets of a set or sliding attack generation. Multiplication of certain pattern has some applications as well, most likely to calculate hash-indicies of masked occupancies.
Derived from Bitwise
Unlike bitwise boolean operations on 64-bit words, which are in fact 64 parallel operations on each bit without any interaction between them, arithmetic operations like addition need to propagate possible carries from lower to higher bits. Despite, Add and Sub are usually as fast their bitwise boolean counterparts, because they are implemented in Hardware within the ALU of the CPU. A so called half-adder to add two bits (A, B), requires an And-Gate for the carry (C) and a Xor-Gate for the sum (S):
two_bitsum = (bitA ^ bitB) | ((bitA & bitB) << 1);
To get an idea of the "complexity" of a simple addition, and how to implement an carry-lookahead adder in software with bitwise boolean and shift instructions only, and presumption on parallel prefix algorithms, this is how a 64-bit Kogge-Stone adder would look like in C:
U64 koggeStoneAdd(U64 a, U64 b) {
U64 gen = a&b; // carries
U64 pro = a^b; // sum
gen |= pro & (gen << 1);
pro = pro & (pro << 1);
gen |= pro & (gen << 2);
pro = pro & (pro << 2);
gen |= pro & (gen << 4);
pro = pro & (pro << 4);
gen |= pro & (gen << 8);
pro = pro & (pro << 8);
gen |= pro & (gen <<16);
pro = pro & (pro <<16);
gen |= pro & (gen <<32);
return a^b ^ (gen << 1);
}
Addition
Addition might be used instead of bitwise 'xor' or 'or' for a union of disjoint (intersection zero) sets, which may yield to simplification of the surrounding expression or may take advantage of certain address calculation instruction such as x86 load effective address (lea).
The enriched algebra with arithmetical and bitwise-boolean operations becomes aware with following relation - the bitwise overflows are the intersection, otherwise the sum modulo two is the symmetric difference - thus the arithmetical sum is the xor-sum plus the carries shifted left one:
x + y = (x ^ y) + 2*(x & y) x ^ y = x + y - 2*(x & y)
This is particular interesting in SWAR-arithmetic, or if we like to compute the average without possible temporary overflows:
(x + y) / 2 = ((x ^ y)>>1) + (x & y)
x86-mnemonics
add rax, rbx ; rax += rbx lea rax, [rcx + rdx + const ] ; rax = rcx + rdx + const
Subtraction
Subtraction (like xor) might be used to implement the relative complement, of a subset inside it's superset. As mentioned, subtraction may be useful in calculating sliding attacks.
x86-mnemonics
sub rax, rbx ; rax -= rbx
The Two's Complement
A lot of bit-twiddling tricks on bitboards to traverse or isolate subsets, rely on two's complement arithmetic. Most recent processors (and compiler or interpreter for these processors) use the two's complement to implement the unary minus operator for signed as well for unsigned integer types. In C it is guaranteed for unsigned integer types. Java guarantees two's complement for all implicit signed integral types char, short, int, long.
x86-mnemonics
neg rax; rax = -rax; rax *= -1
2^N is used as power operator in this paragraph not xor !
Increment of Complement
The two's complement is defined as a value, we need to add to the original value to get 264 which is an "overflowed" zero - since all 64-bit values are implicitly modulo 264. Thus, the two's complement is defined as ones' complement plus one:
-x == ~x + 1
That fulfills the condition that x + (-x) == 2bitsize (264) which overflows to zero:
x + (-x) == 0 x + ~x + 1 == 0 ==> x + ~x == -1 the universal set
Complement of Decrement
Replacing x by x - 1 in the increment of complement formula, leaves another definition - two's complement or Negation is also the ones' complement of the ones' decrement:
-x == ~(x - 1)
Thus, we can reduce subtraction by addition and ones' complement:
~(x - y) == ~x + y x - y == ~(~x + y)
Bitwise Copy/Invert
The two's complement may also defined by a bitwise copy-loop from right (LSB) to left (MSB):
Copy bits from source to destination from right to left - until the first binary "one" is copied. Then invert each of the remaining higher bits.
Signed-Unsigned
This works independently whether we interpret 'x' as signed or unsigned. While 0 is is the synonym for all bits clear, -1 is the synonym for all bits set in a computer word of any arbitrary bit-size, also for 64-bit words such as bitboards.
The signed-unsigned "independence" of the two's complement is the reason that processors don't need different add or sub instructions for signed or unsigned integers. The binary pattern of the result is the same, only the interpretation differs and processors flag different overflow- or underflow conditions simultaneously.
Unsigned 64-bit values as used for bitboards have this value range:
hexadecimal decimal pow2
0x0000000000000000 0 0
0x0000000000000001 1 1
..
0x7fffffffffffffff 9,223,372,036,854,775,807 2^63 - 1
0x8000000000000000 9,223,372,036,854,775,808 2^63
..
0xffffffffffffffff 18,446,744,073,709,551,615 2^64 - 1
With signed interpretation, the positive numbers are subset of the unsigned with MSB clear:
hexadecimal decimal pow2
0x0000000000000000 0 0
0x0000000000000001 1 1
..
0x7fffffffffffffff 9,223,372,036,854,775,807 2^63 - 1
Negative numbers have MSB set to one, thus the sign bit interpretation
hexadecimal decimal pow2
0x8000000000000000 -9,223,372,036,854,775,808 -(2^63)
0x8000000000000001 -9,223,372,036,854,775,807 -(2^63) +1
..
0xfffffffffffffffe -2 -2
0xffffffffffffffff -1 -1
There is no "negative" zero. What makes the value range of negative values one greater than the positive numbers - and implies that
-0x8000000000000000 == 0x8000000000000000
Least Significant One
At some point bitboards require serialization, thus isolation of single populated sub-sets which are power of two values if interpreted as number. Dependent on the bitboard-api those values need a further log2(powOfTwo) to convert them into the square index range from 0 to 63. Bitwise boolean operations (and, xor, or) with two's complement or ones' decrement can compute relatives of a set x in several useful ways.
Isolation
The intersection of a none empty bitboard with it's two's complement isolates the LS1B:
LS1B_of_x = x & -x;
With some arbitrary sample set:
x & -x = LS1B_of_x
. . . . . . . . 1 1 1 1 1 1 1 1 . . . . . . . .
. . 1 . 1 . . . 1 1 . 1 . 1 1 1 . . . . . . . .
. 1 . . . 1 . . 1 . 1 1 1 . 1 1 . . . . . . . .
. . . . . . . . 1 1 1 1 1 1 1 1 . . . . . . . .
. 1 . . . 1 . . & 1 . 1 1 1 . 1 1 = . . . . . . . .
. . 1 . 1 . . . . . 1 1 . 1 1 1 . . 1 . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
Some C++ compiler warn -x still unsigned - (0-x) may used to avoid that with no overhead.
x86-mnemonics
x86-64 expansion BMI1 has LS1B bit isolation:
blsi rax, rbx ; BMI1 rax = rbx & -rbx
BMI1-intrinsic _blsi_u32/64
AMD's x86-64 expansion TBM further has a Isolate Lowest Set Bit and Complement instruction, which applies De Morgan's law to get the complement of the LS1B:
blsic rax, rbx ; TBM: rax = ~rbx | (rbx - 1);
Reset
The intersection of a none empty bitboard with it's ones' decrement resets the LS1B [14]:
x_with_reset_LS1B = x & (x-1);
With some arbitrary sample set:
x & (x-1) = x_with_reset_LS1B
. . . . . . . . . . . . . . . . . . . . . . . .
. . 1 . 1 . . . . . 1 . 1 . . . . . 1 . 1 . . .
. 1 . . . 1 . . . 1 . . . 1 . . . 1 . . . 1 . .
. . . . . . . . . . . . . . . . . . . . . . . .
. 1 . . . 1 . . & . 1 . . . 1 . . = . 1 . . . 1 . .
. . 1 . 1 . . . 1 1 . . 1 . . . . . . . 1 . . .
. . . . . . . . 1 1 1 1 1 1 1 1 . . . . . . . .
. . . . . . . . 1 1 1 1 1 1 1 1 . . . . . . . .
... since we already know two's complement (-x) and ones' decrement (x-1) are complement sets.
x86-mnemonics
x86-64 expansion BMI1 has LS1B bit reset:
blsr rax, rbx ; BMI1 rax = rbx & (rbx - 1)
BMI1-intrinsic _blsr_u32/64
Separation
Masks separated by LS1B by xor with two's complement or ones' decrement. Intersection of one's complement with decrement leaves the below mask excluding LS1B:
above_LS1B_mask = x ^ -x; below_LSB1_mask_including = x ^ (x-1); below_LSB1_mask = ~x & (x-1);
With some arbitrary sample set:
x ^ -x = above_LS1B_mask
. . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
. . 1 . 1 . . . 1 1 . 1 . 1 1 1 1 1 1 1 1 1 1 1
. 1 . . . 1 . . 1 . 1 1 1 . 1 1 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
. 1 . . . 1 . . ^ 1 . 1 1 1 . 1 1 = 1 1 1 1 1 1 1 1
. . 1 . 1 . . . . . 1 1 . 1 1 1 . . . 1 1 1 1 1
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
x ^ (x-1) = below_LSB1_mask_including
. . . . . . . . . . . . . . . . . . . . . . . .
. . 1 . 1 . . . . . 1 . 1 . . . . . . . . . . .
. 1 . . . 1 . . . 1 . . . 1 . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. 1 . . . 1 . . ^ . 1 . . . 1 . . = . . . . . . . .
. . 1 . 1 . . . 1 1 . . 1 . . . 1 1 1 . . . . .
. . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
~x & (x-1) = below_LSB1_mask
1 1 1 1 1 1 1 1 . . . . . . . . . . . . . . . .
1 1 . 1 . 1 1 1 . . 1 . 1 . . . . . . . . . . .
1 . 1 1 1 . 1 1 . 1 . . . 1 . . . . . . . . . .
1 1 1 1 1 1 1 1 . . . . . . . . . . . . . . . .
1 . 1 1 1 . 1 1 & . 1 . . . 1 . . = . . . . . . . .
1 1 . 1 . 1 1 1 1 1 . . 1 . . . 1 1 . . . . . .
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
x86-mnemonics
x86-64 expansion BMI1 has BLSMSK (Mask Up to Lowest Set Bit = below_LSB1_mask_including), AMD's x86-64 expansion TBM has TZMSK (Mask From Trailing Zeros = below_LSB1_mask):
blsmsk rax, rbx ; BMI1: rax = rbx ^ (rbx - 1) tzmsk rax, rbx ; TBM: rax = ~rbx & (rbx - 1)
BMI1-intrinsic _blsmsk_u32/64
Smearing
To smear the LS1B up and down, we use the union with two's complement or ones' decrement:
smearsLS1BUp = x | -x; smearsLS1BDown = x | (x-1);
With some arbitrary sample set:
x | -x = smearsLS1BUp
. . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
. . 1 . 1 . . . 1 1 . 1 . 1 1 1 1 1 1 1 1 1 1 1
. 1 . . . 1 . . 1 . 1 1 1 . 1 1 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
. 1 . . . 1 . . | 1 . 1 1 1 . 1 1 = 1 1 1 1 1 1 1 1
. . 1 . 1 . . . . . 1 1 . 1 1 1 . . 1 1 1 1 1 1
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
x | (x-1) = smearsLS1BDown
. . . . . . . . . . . . . . . . . . . . . . . .
. . 1 . 1 . . . . . 1 . 1 . . . . . 1 . 1 . . .
. 1 . . . 1 . . . 1 . . . 1 . . . 1 . . . 1 . .
. . . . . . . . . . . . . . . . . . . . . . . .
. 1 . . . 1 . . | . 1 . . . 1 . . = . 1 . . . 1 . .
. . 1 . 1 . . . 1 1 . . 1 . . . 1 1 1 . 1 . . .
. . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
. . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
x86-mnemonics
AMD's x86-64 expansion TBM has a Fill From Lowest Set Bit instruction:
blsfill rax, rbx ; TBM: rax = rbx | (rbx - 1)
Least Significant Zero
Dealing with the least significant zero bit (LS0B) or clear bit can be derived from the complement of the LS1B. AMD's x86-64 expansion TBM has six instructions based on boolean operations with the one's increment:
- Isolate Lowest Clear Bit, union with the complement of the increment
- Isolate Lowest Clear Bit and Complement, intersection of the complement with the increment
- Fill From Lowest Clear Bit, intersection with the increment
- Mask From Lowest Clear Bit, exclusive or with the increment
- Set Lowest Clear Bit, union with the increment
- Inverse Mask From Trailing Ones, union of complement and increment
Most Significant One
The MS1B is not that simple to isolate as long we have no reverse arithmetic with carries propagating from left to right. To isolate MS1B, one needs to set all lower bits below MS1B, shift the resulting mask right by one and finally add one. Setting all lower bits in the general case requires 63 times x |= x >> 1 which might be done in parallel prefix manner in log2(64) = 6 steps:
x |= x >> 32; x |= x >> 16; x |= x >> 8; x |= x >> 4; x |= x >> 2; x |= x >> 1; MS1B = (x >> 1) + 1;
Still quite expensive - better to traverse sets the other way around or rely on intrinsic functions to use special processor instructions like BitScanReverse or LeadingZeroCount, which implicitly performs not only the isolation but also the log2.
Common MS1B
Two sets have a common MS1B, if the intersection is greater than the xor sum:
if ((a & b) > (a ^ b)) -> a and b have common MS1B
This is because a common MS1B is set in the intersection but cleared in the xor sum. Otherwise, with no common MS1B, the xor-sum is greater except equal for two zero operands.
Multiplication
64-bit Multiplication has become awfully fast on recent processors. Shift left is of course still faster than multiplication by power of two, but if we have more than one bit set in a factor, it already makes sense to replace for instance
y = (x << 8) + (x << 16);
by
y = x * 0x00010100;
Fill-Multiplication
In fact, we can replace parallel prefix left shifts like,
x |= x << 32; x |= x << 16; x |= x << 8;
where x has max one bit per file, and we can therefor safely replace 'or' by 'add'
x += x << 32; x += x << 16; x += x << 8;
by multiplication with 0x0101010101010101 (which is the A-File in little endian mapping):
. . . . . . . . 1 . . . . . . . . 1 1 . 1 1 . . . . . . . . . . 1 . . . . . . . . 1 1 . 1 1 . . . . . . . . . . 1 . . . . . . . . 1 1 . 1 1 . . . . . . . . . . 1 . . . . . . . . 1 1 . 1 1 . . . 1 . . . 1 . . * 1 . . . . . . . = . 1 1 . 1 1 . . . . 1 . 1 . . . 1 . . . . . . . . . 1 . 1 . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . .
See Kindergarten-Bitboards- or Magic-Bitboards as applications of fill-multiplication.
De Bruijn Multiplication
Another bitboard related application of multiplication is to determine the bit-index of the least significant one bit. A isolated, single bit is multiplied with a De Bruijn Sequence to implement a bitscan.
Division
64-bit Division is still a slow instruction which takes a lot of cycles - it should be avoided at runtime. Division by a power of two is done by right shift.
An interesting application to calculate various masks for delta swaps, e.g. swapping bits, bit-duos, nibbles, bytes, words and double words, is the 2-adic division of the universal set (-1) by 2^(2^i) plus one, which may be done at compile time:
-1 / ( 2^(2^0) + 1) == -1 / ( 2 + 1) == 0x5555555555555555 -1 / ( 2^(2^1) + 1) == -1 / ( 4 + 1) == 0x3333333333333333 -1 / ( 2^(2^2) + 1) == -1 / ( 16 + 1) == 0x0f0f0f0f0f0f0f0f -1 / ( 2^(2^3) + 1) == -1 / ( 256 + 1) == 0x00ff00ff00ff00ff -1 / ( 2^(2^4) + 1) == -1 / ( 65536 + 1) == 0x0000ffff0000ffff -1 / ( 2^(2^5) + 1) == -1 / (4294967296 + 1) == 0x00000000ffffffff
See generalized flipping, mirroring and reversion. Often used masks and factors are the 2-adic division of the universal set (-1) by 2^(2^i) minus one, which results in the lowest bit of SWAR-wise bits set, bit-duos, nibbles, bytes, words and double words:
-1 / ( 2^(2^0) - 1) == -1 / ( 2 - 1) == 0xffffffffffffffff -1 / ( 2^(2^1) - 1) == -1 / ( 4 - 1) == 0x5555555555555555 -1 / ( 2^(2^2) - 1) == -1 / ( 16 - 1) == 0x1111111111111111 -1 / ( 2^(2^3) - 1) == -1 / ( 256 - 1) == 0x0101010101010101 -1 / ( 2^(2^4) - 1) == -1 / ( 65536 - 1) == 0x0001000100010001 -1 / ( 2^(2^5) - 1) == -1 / (4294967296 - 1) == 0x0000000100000001
Modulo
Modular arithmetic with 64-bit modulo by a constant, has applications in Cryptography [15], Hashing, and with Bitboards in Bit Scanning, Population Count and Congruent Modulo Bitboards for Sliding Piece Attacks.
Casting out 255
Similar to Casting out nines with decimals and due to the congruence relation
Basen ≡ 1 (mod Base-1)
casting out 255 can be used to add all the eight bytes within a SWAR-wise 64-bit quad word if the sum is less than 255, as mentioned, applicable in Population Count and Congruent Modulo Bitboards - Casting out 255.
Reciprocal Multiplication
Likely 64-bit compiler will optimize modulo (and division) by reciprocal, 2^64 div constant, to perform a 64*64 = 128bit fixed point multiplication to get the quotient in the upper 64-bit, and a second multiplication and subtraction to finally get the remainder. Here some sample x86-64 assembly:
r11d := r10 % 257 mov r11d, r10 ; masked diagonal mov rax, ff00ff00ff00ff01H ; 2^(64+8) / 257 mul r10 shr rdx, 8 imul edx, 257 ; 00000101H sub r11d, edx
Power of Two
As a remainder, and to close the cycle to bitwise boolean operations, the well known trick is mentioned, to replace modulo by power of two by intersection with power of two minus one:
a % 2n == a & (2n - 1)
Selected Publications
1847 ...
- George Boole (1847). The Mathematical Analysis of Logic, Being an Essay towards a Calculus of Deductive Reasoning. Macmillan, Barclay & Macmillan
- George Boole (1848). The Calculus of Logic. Cambridge and Dublin Mathematical Journal, Vol. III
- Augustus De Morgan (1860). Syllabus of a Proposed System of Logic. Walton & Malbery
- Charles S. Peirce (1867). On an Improvement in Boole's Calculus of Logic. Proceedings of the American Academy of Arts and Sciences, Series Vol. 7
- Georg Cantor (1874). Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen. Journal für die reine und angewandte Mathematik, No. 77
- Charles S. Peirce (1880). On the Algebra of Logic. American Journal of Mathematics, Vol. 3
- John Venn (1880). On the Diagrammatic and Mechanical Representation of Propositions and Reasonings. Philosophical Magazine, Vol. 9, No. 5
- John Venn (1881). Symbolic Logic. MacMillan & Co.
1900 ...
- Claude Shannon (1938). A Symbolic Analysis of Relay and Switching Circuits. Transactions of the AIEE, Vol. 57, No 12, Master's thesis 1940, Massachusetts Institute of Technology
- Victor I. Shestakov (1941). Algebra of Two Poles Schemata. Automatics and Telemechanics, Vol. 5, No 2
1950 ...
- Lazar A. Lyusternik, Aleksandr Abramov, Victor I. Shestakov, Mikhail R. Shura-Bura (1952). Programming for High-Speed Electronic Computers. (Программирование для электронных счетных машин)
- Christopher Strachey (1961). Bitwise operations. Communications of the ACM, Vol. 4, No. 3
2000 ...
- Henry S. Warren, Jr. (2002, 2012). Hacker's Delight. Addison-Wesley
- Donald Knuth (2009). The Art of Computer Programming, Volume 4, Fascicle 1: Bitwise tricks & techniques, as Pre-Fascicle 1a postscript
- Ronald L. Rivest (2011). The invertibility of the XOR of rotations of a binary word. International Journal of Computer Mathematics, Vol. 88, 2009 pdf preprint
Forum Posts
2000 ...
- curiosity killed the cat... hi/lo bit C verses Assembly by Dann Corbit, CCC, July 17, 2003
- mask of highest bit by Andrew Shapira, CCC, September 21, 2005
2010 ...
- How to Shift Left (by) a Negative Number?? by Steve Maughan, CCC, April 05, 2013
- To shift or not to shift by thevinenator, OpenChess Forum, September 09, 2015 » Space-Time Tradeoff
- Question about resetting a bit in a bitboard corresponding to a given square by guenther, FishCooking, September 09, 2016 » Reset Bit
- On the speed of SquareBB array by protonspring, FishCooking, March 22, 2019
2020 ...
- C++20 standard bit operations by Jon Dart, CCC, November 15, 2020 » Population Count, BitScan, C++
External Links
Sets
- Set (mathematics) from Wikipedia
- Portal:Set theory from Wikipedia
- Finite set from Wikipedia
- Fuzzy set from Wikipedia
- Set theory from Wikipedia
- Naive set theory from Wikipedia
- Zermelo–Fraenkel set theory from Wikipedia » Ernst Zermelo, Abraham Fraenkel
Algebra
- Algebra from Wikipedia
- Elementary algebra from Wikipedia
- Abstract algebra from Wikipedia
- Algebraic structure from Wikipedia (Model theory)
- Algebra of sets from Wikipedia
- Boolean algebra from Wikipedia
- Boolean algebra (logic) from Wikipedia
- Boolean algebra (structure) from Wikipedia
- Boolean algebras canonically defined from Wikipedia
- Boolean ring from Wikipedia
- Finite field from Wikipedia
- GF(2) from Wikipedia
- The Mathematics of Boolean Algebra (Stanford Encyclopedia of Philosophy)
Logic
- Logic from Wikipedia
- Portal:Logic from Wikipedia
- Mathematical logic from Wikipedia
- Algebraic logic from Wikipedia
- Propositional calculus from Wikipedia
- Predicate logic from Wikipedia
- Entailment from Wikipedia
- Syllogism from Wikipedia
- Logical connective from Wikipedia
Operations
Setwise
- Intersection (set theory) from Wikipedia
- Union (set theory) from Wikipedia
- Complement (set theory) from Wikipedia
Bitwise
- Logical conjunction from Wikipedia
- Logical disjunction from Wikipedia
- Exclusive or from Wikipedia
- Negation from Wikipedia
- Bit Shifts from Wikipedia
- Circular shift from Wikipedia
Arithmetic
- Addition from Wikipedia
- Subtraction from Wikipedia
- Two's complement from Wikipedia
- Multiplication from Wikipedia
- Division from Wikipedia
- Modulo operation from Wikipedia
Modular arithmetic
- Congruence relation from Wikipedia
- Modular arithmetic from Wikipedia
- Linear congruence theorem from Wikipedia
Misc
- Casiopea - Conjunction, Perfect Live (1986), YouTube Video
- Hux Flux - Bitshifter, Division by Zero, YouTube Video
References
- ↑ Wassily Kandinsky - Upward, 1929, Peggy Guggenheim Collection, Wikimedia COmmons
- ↑ Andrey Ershov, Mikhail R. Shura-Bura (1980). The Early Development of Programming in the USSR. in Nicholas C. Metropolis (ed.) A History of Computing in the Twentieth Century. Academic Press, preprint pp. 43
- ↑ Lazar A. Lyusternik, Aleksandr A. Abramov, Victor I. Shestakov, Mikhail R. Shura-Bura (1952). Programming for High-Speed Electronic Computers. (Программирование для электронных счетных машин)
- ↑ John Venn (1880). On the Diagrammatic and Mechanical Representation of Propositions and Reasonings. Philosophical Magazine, Vol. 9, No. 59
- ↑ Greater or less in the arithmetical sense is usually not relevant with bitboards, but see greater condition in Thor's Hammer's move generation
- ↑ George Boole (1847). The Mathematical Analysis of Logic, Being an Essay towards a Calculus of Deductive Reasoning. Macmillan, Barclay & Macmillan
- ↑ Charles S. Peirce (1880). On the Algebra of Logic. American Journal of Mathematics, Vol. 3
- ↑ Augustus De Morgan (1860). Syllabus of a Proposed System of Logic. Walton & Malbery
- ↑ Marvin Minsky, Seymour Papert (1969, 1972). Perceptrons: An Introduction to Computational Geometry. The MIT Press, ISBN 0-262-63022-2
- ↑ Re: Java chess program? by Moritz Berger, rgcc, May 29, 1997 » Shifting Bitboards, Java
- ↑ To shift or not to shift by thevinenator, OpenChess Forum, September 09, 2015
- ↑ On the speed of SquareBB array by protonspring, FishCooking, March 22, 2019
- ↑ Donald Knuth (2009). The Art of Computer Programming, Volume 4, Fascicle 1: Bitwise tricks & techniques, as Pre-Fascicle 1a postscript
- ↑ Peter Wegner (1960). A technique for counting ones in a binary computer. Communications of the ACM, Volume 3, 1960
- ↑ Modular exponentiation from Wikipedia