De Bruijn Sequence
Home * Programming * Data * De Bruijn Sequence
In combinatorial mathematics, a k-ary De Bruijn Sequence B(k, n) of order n, named after the Dutch mathematician Nicolaas de Bruijn, is a cyclic sequence of a given alphabet A with size k for which every possible subsequence of length n in A appears as a sequence of consecutive characters exactly once [1]. In chess programming there are applications of de Bruijn sequences with the Binary alphabet, in hashing sets like Piece-Sets or Square-sets, also called Bitboards, most notably in Bit scanning [2] .
Contents
Binary alphabet
According to De Bruijn himself [3] , the existence of De Bruijn sequences were first proved, for the case of alphabets with two elements, by Camille Flye Sainte-Marie in 1894, whereas the generalization to larger alphabets is originally due to Tanja van Ardenne-Ehrenfest [4] and himself.
Binary digits or bits inside a computer word are B(2, n) de Bruijn sequences, with 2n bits length and equal number of ones and zeros, with 2n overlapping unique n-bit subsequences. Since the sequences are cyclic and n-1 subsequences need to wrap, we restrict them to at least n-1 leading zeros, to make them overlap the hidden trailing "zeros".
Odd sequences have n leading zeros. The even ones with n-1 leading zeros are rotated (shifted) left by one. Due to n leading zeros of these odd sequences we further consider, the first subsequence[0] is zero. Due to the overlapping, each subsequence[i+1] is dependent from subsequence[i]. The doubled value incremented by either zero or one. Since subsequence[0] is zero, a second zero subsequence with six consecutive binary zeros is further prohibited, and subsequence[1] must be one. Subsequence index i is counted from most significant bit left to right, and therefor reversed from usual bit-index. A modulo 2n restricts all subsequences to n bits:
s[i+1] = (2s[i] + (0|1)) mod (2n)
The Cardinality of all distinct B(2, n) de Bruijn sequences is:
|B(2, n)| = 2(2n-1 - n)
| n | 2n-1 - n | B(2, n)| |
|---|---|---|
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 2 |
| 4 | 4 | 16 |
| 5 | 11 | 2,048 |
| 6 | 26 | 67,108,864 |
| 7 | 57 | 144,115,188,075,855,872 |
| 8 | 120 | ~1.329e+36 |
B(2, 1)
The two one-bit subsequences obviously do not overlap:
i 01 s[i] 0 0 0 1 1 1
B(2, 2)
B(2, 2) implies 22 or 4-bit sequences. There is one odd four-bit de Bruijn sequence with four overlapping unique two-bit subsequences, 0x3.
i 0011|0 s[i] 0 00 . . . 0 1 01 1 2 . 11 . . 3 3 1|0 2
B(2, 3)
B(2, 3) implies 23 or 8-bit sequences. There are two odd eight-bit sequences with eight overlapping unique three-bit subsequences, 0x17 and 0x1d. Note that the five relevant bits are reversed.
i 00010111|00 s[i] i 00011101|00 s[i] 0 000 . . . . 0 0 000 . . . . 0 1 001 1 1 001 1 2 . 010 . . . 2 2 . 011 . . . 3 3 101 5 3 111 7 4 . . 011 . . 3 4 . . 110 . . 6 5 111 7 5 101 5 6 . . . 11|0 6 6 . . . 01|0 2 7 1|00 4 7 1|00 4
B(2, 4)
B(2, 4) implies 24 or 16 bit sequences. There are 16 odd 16-bit sequences with 16 overlapping unique four-bit subsequences:
0x09af 0000100110101111 0x09eb 0000100111101011 0x0a6f 0000101001101111 0x0a7b 0000101001111011 0x0b3d 0000101100111101 0x0b4f 0000101101001111 0x0bcd 0000101111001101 0x0bd3 0000101111010011 0x0cbd 0000110010111101 0x0d2f 0000110100101111 0x0d79 0000110101111001 0x0de5 0000110111100101 0x0f2d 0000111100101101 0x0f4b 0000111101001011 0x0f59 0000111101011001 0x0f65 0000111101100101
for instance 0x0d2f:
i 0000110100101111|000 s[i] 0 0000 . . . . . . . . 0 1 0001 1 2 . 0011 . . . . . . . 3 3 0110 6 4 . . 1101 . . . . . . 13 5 1010 10 6 . . . 0100 . . . . . 4 7 1001 9 8 . . . . 0010 . . . . 2 9 0101 5 10 . . . . . 1011 . . . 11 11 0111 7 12 . . . . . . 1111 . . 15 13 111|0 14 14 . . . . . . . 11|00 12 15 1|000 8
B(2, 5)
B(2, 5) implies 25 or 32 bit sequences. There are 2^11 or 2,048 odd 32-bit sequences with 32 overlapping unique five-bit subsequences, for instance 0x076be629
i 00000111011010111110011000101001|0000 s[i] 0 00000 . . . . . . . . . . . . . . . . 0 1 00001 1 2 . 00011 . . . . . . . . . . . . . . . 3 3 00111 7 4 . . 01110 . . . . . . . . . . . . . . 14 5 11101 29 6 . . . 11011 . . . . . . . . . . . . . 27 7 10110 22 8 . . . . 01101 . . . . . . . . . . . . 13 9 11010 26 10 . . . . . 10101 . . . . . . . . . . . 21 11 01011 11 12 . . . . . . 10111 . . . . . . . . . . 23 13 01111 15 14 . . . . . . . 11111 . . . . . . . . . 31 15 11110 30 16 . . . . . . . . 11100 . . . . . . . . 28 17 11001 25 18 . . . . . . . . . 10011 . . . . . . . 19 19 00110 6 20 . . . . . . . . . . 01100 . . . . . . 12 21 11000 24 22 . . . . . . . . . . . 10001 . . . . . 17 23 00010 2 24 . . . . . . . . . . . . 00101 . . . . 5 25 01010 10 26 . . . . . . . . . . . . . 10100 . . . 20 27 01001 9 28 . . . . . . . . . . . . . . 1001|0. . 18 29 001|00 4 30 . . . . . . . . . . . . . . . 01|000 8 31 1|0000 16
B(2, 6)
B(2, 6) implies 26 or 64 bit sequences. There are 2^26 or 67,108,864 odd 64-bit sequences with 64 overlapping unique six-bit subsequences, for instance 0x022fdd63cc95386d
i 0000001000101111110111010110001111001100100101010011100001101101|00000 s[i] 0 000000 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0 1 000001 1 2 . 000010 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 3 000100 4 4 . . 001000 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 5 010001 17 6 . . . 100010 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 7 000101 5 8 . . . . 001011 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 9 010111 23 10 . . . . . 101111 . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 11 011111 31 12 . . . . . . 111111 . . . . . . . . . . . . . . . . . . . . . . . . . . 63 13 111110 62 14 . . . . . . . 111101 . . . . . . . . . . . . . . . . . . . . . . . . . 61 15 111011 59 16 . . . . . . . . 110111 . . . . . . . . . . . . . . . . . . . . . . . . 55 17 101110 46 18 . . . . . . . . . 011101 . . . . . . . . . . . . . . . . . . . . . . . 29 19 111010 58 20 . . . . . . . . . . 110101 . . . . . . . . . . . . . . . . . . . . . . 53 21 101011 43 22 . . . . . . . . . . . 010110 . . . . . . . . . . . . . . . . . . . . . 22 23 101100 44 24 . . . . . . . . . . . . 011000 . . . . . . . . . . . . . . . . . . . . 24 25 110001 49 26 . . . . . . . . . . . . . 100011 . . . . . . . . . . . . . . . . . . . 35 27 000111 7 28 . . . . . . . . . . . . . . 001111 . . . . . . . . . . . . . . . . . . 15 29 011110 30 30 . . . . . . . . . . . . . . . 111100 . . . . . . . . . . . . . . . . . 60 31 111001 57 32 . . . . . . . . . . . . . . . . 110011 . . . . . . . . . . . . . . . . 51 33 100110 38 34 . . . . . . . . . . . . . . . . . 001100 . . . . . . . . . . . . . . . 12 35 011001 25 36 . . . . . . . . . . . . . . . . . . 110010 . . . . . . . . . . . . . . 50 37 100100 36 38 . . . . . . . . . . . . . . . . . . . 001001 . . . . . . . . . . . . . 9 39 010010 18 40 . . . . . . . . . . . . . . . . . . . . 100101 . . . . . . . . . . . . 37 41 001010 10 42 . . . . . . . . . . . . . . . . . . . . . 010101 . . . . . . . . . . . 21 43 101010 42 44 . . . . . . . . . . . . . . . . . . . . . . 010100 . . . . . . . . . . 20 45 101001 41 46 . . . . . . . . . . . . . . . . . . . . . . . 010011 . . . . . . . . . 19 47 100111 39 48 . . . . . . . . . . . . . . . . . . . . . . . . 001110 . . . . . . . . 14 49 011100 28 50 . . . . . . . . . . . . . . . . . . . . . . . . . 111000 . . . . . . . 56 51 110000 48 52 . . . . . . . . . . . . . . . . . . . . . . . . . . 100001 . . . . . . 33 53 000011 3 54 . . . . . . . . . . . . . . . . . . . . . . . . . . . 000110 . . . . . 6 55 001101 13 56 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 011011 . . . . 27 57 110110 54 58 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101101 . . . 45 59 01101|0 26 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1101|00 . 52 61 101|000 40 62 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 01|0000 16 63 1|00000 32
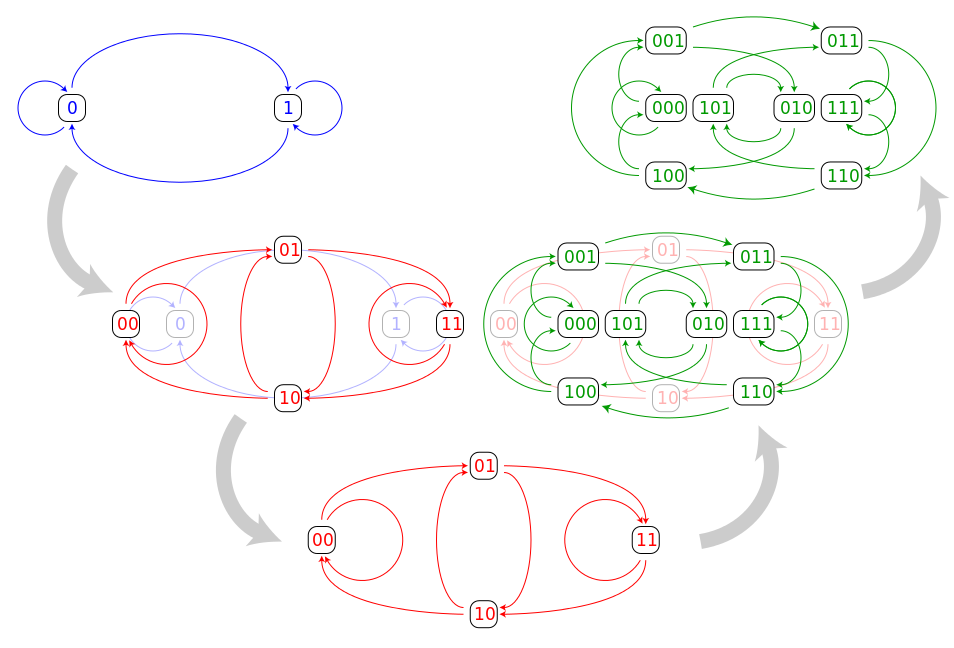
De Bruijn Graphs
A De Bruijn graph is a directed graph representing overlaps between sequences of symbols [5] .
- Each vertex has exactly m incoming and m outgoing edges
- Each n-dimensional de Bruijn graph is the line digraph of the (n-1)-dimensional de Bruijn graph
- Each de Bruijn graph is Eulerian and Hamiltonian. The Euler cycles and Hamiltonian cycles of these graphs are de Bruijn sequences.
The graph construction of the three smallest binary de Bruijn graphs
B(2, 4) Graph
- A De Bruijn graph. Every four-digit sequence occurs exactly once if one
- traverses every edge exactly once and returns to one's starting point.
De Bruijn Graph on a Chess Board
A directed De Bruijn Graph of B(2, 6) sequences with Little-Endian Rank-File Mapping board coordinates (a1 = 0, b1 = 1, h8 = 63). For topology reasons, almost each node (except a1 and h8) of the graph is deconcentrated and appears twice in the form of two reversed binary trees. The leaf outputs join the respective reversed tree. Between c6 and f3 is a direct cycle, since 42 is 2*21 and 21 is (2*42 + 1) % 64, with both six-bit pattern reversed - 010101 (21) versus 101010 (42). The challenge is to traverse the graph in any way to visit each of the 64 nodes aka squares exactly once.
+----------------->---------------a1--------------<-----------------+
| | |
| b1 |
| +--------------/ \-------------+ |
| c1 d1 |
^ +-----/ \-----+ +-----/ \-----+ |
| e1 f1 g1 h1 |
| +-/ \-+ +-/ \-+ +-/ \-+ +-/ \-+ |
| a2 b2 c2 d2 e2 f2 g2 h2 |
| a3 b3 c3 d3 e3 |f3| g3 h3 a4 b4 c4 d4 e4 f4 g4 h4 |
+-a5b5c5d5e5f5g5h5a6b6c6d6e6f6g6h6 a7b7c7d7e7f7g7h7a8b8c8d8e8f8 | |
^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ | |
| |
+----------------->---------------h8--------------<--------------+ ^
| | |
| g8 |
| +--------------/ \-------------+ |
| f8 e8 |
^ +-----/ \-----+ +-----/ \-----+ |
| d8 c8 b8 a8 |
| +-/ \-+ +-/ \-+ +-/ \-+ +-/ \-+ |
| h7 g7 f7 e7 d7 c7 b7 a7 |
| h6 g6 f6 e6 d6 |c6| b6 a6 h5 g5 f5 e5 d5 c5 b5 a5--+
+-h4g4f4e4d4c4b4a4h3g3f3e3d3c3b3a3 h2g2f2e2d2c2b2a2h1g1f1e1d1c1
^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^
De Bruijn Networks
So called De Bruijn Networks with the topology of De Bruijn Graphs have interesting properties in processor and computer networks, for instance as described by Feldmann et al. to connect Transputer networks [6] [7] .
See also
- Nicolaas de Bruijn
- De Bruijn Multiplication from BitScan
- De Bruijn Sequence Generator
- Prouhet–Thue–Morse Sequence
- Pseudorandom Number Generator
Selected Publications
1894
- Camille Flye Sainte-Marie (1894). Solution to question nr. 48, L'Intermédiaire des Mathématiciens 1, reproduced in Nicolaas de Bruijn (1975). Acknowledgement of priority to C. Flye Sainte-Marie on the counting of circular arrangements of 2n zeros and ones that show each n-letter word exactly once. Technical Report, Technische Hogeschool Eindhoven, pdf
1946
- Nicolaas de Bruijn (1946). A Combinatorial Problem. Koninklijke Nederlandse Akademie v. Wetenschappen 49: 758–764.
- Jack Good (1946). Normal Recurring Decimals. Journal of the London Mathematical Society [8]
1950 ...
- Lester Randolph Ford, Jr. (1957). A Cyclic Arrangement of M-Tuples. Report No. P-1071. Rand Corporation
- Solomon W. Golomb (1967, 1982). Shift Register Sequences. Holden-Day Inc., revised 2nd edition, Aegean Park Press
- Harold M. Fredricksen (1968). Disjoint Cycles from the de Bruijn Graph. Ph.D. thesis, University of Southern California, advisor Solomon Wolf Golomb
1970 ...
- Harold M. Fredricksen (1970). The lexicographically least de Bruijn cycle. Journal of Combinatorial Theory, Vol. 9, No. 1
- Abraham Lempel (1970). On a Homomorphism of the De Bruijn Graph and Its Applications to the Design of Feedback Shift Registers. IEEE Transactions on Computers, Vol. 19, No. 12
- Harold M. Fredricksen (1972). Generation of the Ford Sequence of Length 2n, n Large. JPL Technical Report 32-1526, Vol. IV, pdf
1990 ...
- Yuejiang Huang (1990). A new algorithm for the generation of binary de Bruijn sequences. Journal of Algorithms, Vol. 11, No. 1
- Chris J. Mitchell, Tuvi Etzion, Kenneth G. Paterson (1996). A method for constructing decodable de Bruijn Sequences. pdf via CiteSeerX
- Fred S. Annexstein (1997). Generating De Bruijn Sequences: An Efficient Implementation. IEEE Transactions on Computers, Vol. 46, No. 2, pdf, Supplement: C-code implementation
- Charles E. Leiserson, Harald Prokop, Keith H. Randall (1998). Using de Bruijn Sequences to Index a 1 in a Computer Word. pdf
2000 ...
- Vladimir Raphael Rosenfeld (2002). Enumerating De Bruijn Sequences. Institute of Evolution, University of Haifa, pdf
- Vladimir Raphael Rosenfeld (2002). Enumerating Kautz Sequences. Institute of Evolution, University of Haifa, pdf
- Anwitaman Datta, Sarunas Girdzijauskas, Karl Aberer (2004). On de Bruijn routing in distributed hash tables: There and back again. P2P2004, The 4th IEEE International Conference on Peer-to-Peer Computing, pdf
- Pierre Fraigniaud, Philippe Gauron (2005). D2B: a de Bruijn Based Content-Addressable Network. pdf
- Drew Armstrong (2006). De Bruijn Sequences. pdf
- Jean Berstel, Dominique Perrin (2007). The origins of combinatorics on words. European Journal of Combinatorics 28, pdf
2010 ...
- Yaw-Ling Lin, Charles B. Ward, Bharat Jain, Steven Skiena (2011). Constructing Orthogonal de Bruijn Sequences. LNCS 6844, WADS 2011
- Zuling Chang, Martianus Frederic Ezerman, San Ling, Huaxiong Wang (2016). On Binary de Bruijn Sequences from LFSRs with Arbitrary Characteristic Polynomials. arXiv:1611.10088 [9]
- Zuling Chang, Martianus Frederic Ezerman, Adamas Aqsa Fahreza, San Ling, Huaxiong Wang (2017). Large Order Binary de Bruijn Sequences via Zech's Logarithms. arXiv:1705.03150 [10]
- Joe Sawada, Aaron Williams (2017). Practical Algorithms to Rank Necklaces, Lyndon Words, and de Bruijn Sequences. Journal of Discrete Algorithms, Vol. 43, No. C, pdf
External Links
- De Bruijn sequence from Wikipedia
- De Bruijn graph from Wikipedia
- Kautz graph from Wikipedia
- Koorde from Wikipedia
- A166315 - OEIS
- Lyndon word from Wikipedia
- If - Forgotten Roads, Beat-Club #71, September 25, 1971, YouTube Video
References
- ↑ De Bruijn sequence from Wikipedia
- ↑ Charles E. Leiserson, Harald Prokop, Keith H. Randall (1998). Using de Bruijn Sequences to Index a 1 in a Computer Word. pdf
- ↑ Nicolaas de Bruijn (1975). Acknowledgement of priority to C. Flye Sainte-Marie on the counting of circular arrangements of 2n zeros and ones that show each n-letter word exactly once. Technical Report, Technische Hogeschool Eindhoven, pdf
- ↑ Nicolaas de Bruijn (1985). In Memoriam T. van Ardenne-Ehrenfest. pdf
- ↑ De Bruijn graph from Wikipedia
- ↑ Rainer Feldmann, Peter Mysliwietz, Burkhard Monien (1991). A Fully Distributed Chess Program. Advances in Computer Chess 6, pdf
- ↑ Rainer Feldmann (1993). Game Tree Search on Massively Parallel Systems Phd-Thesis, pdf
- ↑ Recurring decimal from Wikipedia
- ↑ LFSR from Wikipedia
- ↑ Zech's logarithm from Wikipedia