MAPP
Home * Knowledge * Cognition * MAPP
MAPP, (Memory-aided Pattern Perceiver)
a program by Kevin J. Gilmartin and Herbert Simon to simulate the chess board reconstruction task examined by William Chase and Herbert Simon [1]. MAPP contains a learning component to acquire and store a large set of configurations of chess pieces and a performance component to carry out the the board reconstruction task. From Miller's chunking hypothesis [2], EPAM theory, and the limited capacity of short-term memory, one would predict that a chessboard can be reconstructed from information held in short-term memory if, and only if, it can be encoded in not more than about seven familiar perceptual chunks. If a single piece on a particular square constitutes a chunk for the subject, then it should be able to recall only about seven pieces. If it can recall the positions of more than twenty pieces, then it must be that each chunk consists, on average, of a configuration of about three pieces [3].
Contents
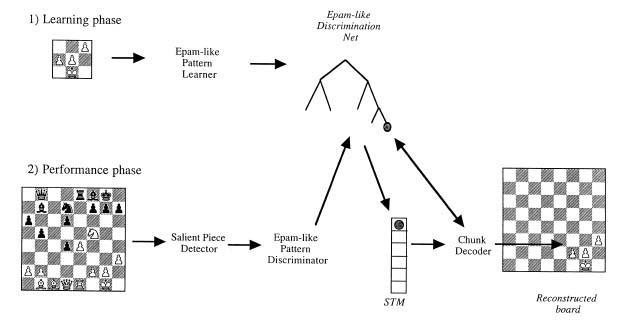
Schematic Representation
A schematic representation of the principle components of MAPP shows the learning and performance
processes used to reconstruct a chess position [4]
Perception
When a chess position is presented, a simplified version of the eye movement simulation program Perceiver is used to scan the board in order to notice the pieces and their relations. When a piece is fixated (salient piece), an EPAM-like discrimination process seeks to recognize cluster of pieces surrounding the fixated piece as a familar chunk. If it is successful, the symbol designating this chunk is stored in short-term memory. This process is repeated at successive points of fixation until no more pieces become salient or memory capacity is reached (no more than seven chunks).
Reconstruction
In the reconstruction phase, the EPAM net is used to decode the symbols held in short-term memory into locational information for each of the pieces in a chunk. In various experiments, MAPP was able to reconstruct positions with 73% accuracy [5] [6].
See also
Publicatons
- Herbert Simon, Kevin J. Gilmartin (1973). A Simulation of Memory for Chess Positions. Cognitive Psychology, Vol. 5, No. 1, reprinted in Herbert Simon (1979). Models of Thought, Yale University Press
- Herbert Simon, William Chase (1973). Skill in Chess. American Scientist, Vol. 61, No. 4, reprinted in David Levy (ed.) (1988) Computer Chess Compendium, pdf
- Neil Charness (1976). Memory for Chess Positions: Resistance to Interference. Journal of Experimental Psychology: Human Learning and Memory, Vol. 2, No. 6
- Michael George, Jonathan Schaeffer (1990). Chunking for Experience. ICCA Journal, Vol. 13, No. 3, pdf
- Fernand Gobet (2005). Chunking Models of Expertise: Implications for Education. Applied Cognitive Psychology, Vol. 19, No. 2
References
- ↑ William Chase, Herbert Simon (1973). Perception in chess. Cognitive Psychology, Vol. 4, No. 1
- ↑ George Armitage Miller (1956). The Magical Number Seven, Plus or Minus Two. Psychological Review, Vol. 101, No. 2, pdf
- ↑ Herbert Simon, William Chase (1973). Skill in Chess. American Scientist, Vol. 61, No. 4, pp. 401, reprinted in David Levy (ed.) (1988) Computer Chess Compendium, pdf
- ↑ Expertise in Memory - Evidence for Chunking Theory by Victor Long, Chandra Singh and David Snitkof, Brown University, see also Figure 6 in Herbert Simon, William Chase (1973). Skill in Chess. American Scientist, Vol. 61, No. 4, pp. 401, reprinted in David Levy (ed.) (1988) Computer Chess Compendium, pdf
- ↑ Herbert Simon, Kevin J. Gilmartin (1973). A Simulation of Memory for Chess Positions. Cognitive Psychology, Vol. 5, pp. 29-46
- ↑ Michael George, Jonathan Schaeffer (1990). Chunking for Experience. ICCA Journal, Vol. 13, No. 3, pdf