Parallel Prefix Algorithms
Home * Programming * Algorithms * Parallel Prefix Algorithms
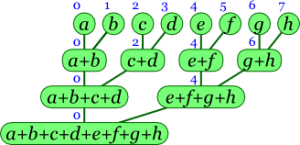
Parallel prefix algorithms compute all prefixes of a input sequence in logarithmic time, and are topic of various SIMD and SWAR techniques applied to bitboards [2] . This page provides some basics on simple parallel prefix problems, like parity words and Gray code with some interesting properties, followed by some theoretical background on more complex parallel prefix problems, like Kogge-Stone by Steffan Westcott, and a comparison of three similar Kogge-Stone routines for different purpose.
Contents
Parity Words
Parity is often related to error detection and correction. The modulo 2 sum aka exclusive or (xor) of any number of inputs is sufficient to determine even or odd parity. On a bitboard for each bit 0..63 we like to know, whether the number of ones including all trailing bits is odd or even, xi is the bit in x with bit-index i:
p0 = x0; p1 = x0 ^ x1; p2 = x0 ^ x1 ^ x2; ... p63 = x0 ^ x1 ^ x2 ^ .... ^ x63;
Or recursively
p[i] = p[i-1] ^ x[i];
p63 indicates whether the whole cardinality is odd or even. The parallel prefix solution looks that way:
x ^= x << 1; x ^= x << 2; x ^= x << 4; x ^= x << 8; x ^= x << 16; x ^= x << 32;
and only need log2(64) == 6 steps to perform all the xor instructions.
Surprisingly, thanks to xor, we can restore the initial value by a final:
x ^= x << 1;
Gray Code
The reflected binary code, or Gray code has some similar properties [3]. The Gray code is defined by the modulo 2 sum or exclusive or of a word with its value shifted right by one.
gray = x ^ (x >> 1);
This ensures that consecutive Gray codes have only one bit changed, that is a Hamming distance of one. For instance for a 4-bit or nibble Gray code:
| x decimal | x binary | x>>1 | Gray bin | decimal |
|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0 |
| 1 | 0001 | 0000 | 0001 | 1 |
| 2 | 0010 | 0001 | 0011 | 3 |
| 3 | 0011 | 0001 | 0010 | 2 |
| 4 | 0100 | 0010 | 0110 | 6 |
| 5 | 0101 | 0010 | 0111 | 7 |
| 6 | 0110 | 0011 | 0101 | 5 |
| 7 | 0111 | 0011 | 0100 | 4 |
| 8 | 1000 | 0100 | 1100 | 12 |
| 9 | 1001 | 0100 | 1101 | 13 |
| 10 | 1010 | 0101 | 1111 | 15 |
| 11 | 1011 | 0101 | 1110 | 14 |
| 12 | 1100 | 0110 | 1010 | 10 |
| 13 | 1101 | 0110 | 1011 | 11 |
| 14 | 1110 | 0111 | 1001 | 9 |
| 15 | 1111 | 0111 | 1000 | 8 |
| 0 | 0000 | 0000 | 0000 | 0 |
Decoding Gray code is a parallel prefix problem similar to the ring-wise operations of the Parity words. For a nibble Gray code:
x = gray; x ^= x >> 2; x ^= x >> 1;
Or for 64-bit Gray-Codes:
x = gray; x ^= x >> 32; x ^= x >> 16; x ^= x >> 8; x ^= x >> 4; x ^= x >> 2; x ^= x >> 1;
Fill Stuff
Parallel prefix front and rear-fills, for instance to determine pawn spans in bitboards, are quite simple to understand.
U64 nortFill(U64 gen) {
gen |= (gen << 8);
gen |= (gen << 16);
gen |= (gen << 32);
return gen;
}
U64 soutFill(U64 gen) {
gen |= (gen >> 8);
gen |= (gen >> 16);
gen |= (gen >> 32);
return gen;
}
This is actually a simplified Kogge-Stone algorithm, whose general form even considers a second bitboard to occlude the flood accordantly.
Elaborations on Kogge-Stone
Elaborations on Kogge-Stone parallel prefix algorithm by Steffan Westcott [4] :
A parallel prefix problem is of the sort:
Given the terms x1, x2, x3, ... , xN and an associative operator #
find the values q1 = x1
q2 = x1 # x2
q3 = x1 # x2 # x3
.
.
.
qN = x1 # x2 # x3 # ... # xN
Associative expressions can be bracketed any way you like, the result is the same. To see why this is interesting for chess programming, let's define x1, x2, ... and # to be
xI = < gI, pI > (a two element tuple)
where gI = square aI has a rook on it
and pI = square aI is empty
for all I = 1, 2, 3, ... , 8
and xI # xJ = < gI, pI > # < gJ, pJ >
= < ((gI && pJ) || gJ), (pI && pJ) >
All this algebra looks very scary at first, so here's an example:
q2 = x1 # x2 = < rook_on_a1, a1_is_empty > # < rook_on_a2, a2_is_empty >
= < ((rook_on_a1 && a2_is_empty) || rook_on_a2),
(a1_is_empty && a2_is_empty) >
- The first tuple of q2 tells us if a rook is on a2 or can move up to a2 along empty squares.
- The second tuple of q2 tells us if a rook could move up freely through a1-a2 ie. a1-a2 are empty.
In general,
xI # x(I+1) # ... # xJ =
< a_rook_somewhere_on_aI_to_aJ_is_either_on_aJ_or_can_move_up_to_aJ,
all_squares_aI_to_aJ_are_empty >
and so
qJ = < a_rook_somewhere_in_file_a_is_either_on_aJ_or_can_move_up_to_aJ,
all_squares_a1_to_aJ_are_empty >
The tuples g and p are known as the "generator" and "propagator" terms in the literature of fast carry propagation circuits. But we are not dealing with carry bits in a carry propagate adder! Here, we are generating and propagating upward rook attacks along a file of a chessboard.
Why all this theory? Well, prefix computation is a heavily researched area, researched by many folk smarter than me :) Its of interest because it has many applications, such as VLSI design, pattern matching, and others. There are many different ways of going about it, with different implementation characteristics.
U64 FillUpOccluded(U64 g, U64 p) {
g |= p & (g << 8);
p &= (p << 8);
g |= p & (g << 16);
p &= (p << 16);
return g |= p & (g << 32);
}
U64 RookAttacksUp(U64 rooks, U64 empty_squares) {
return ShiftUp(FillUpOccluded(rooks, empty_squares));
}
The method chosen in FillUpOccluded() is based on a Kogge-Stone parallel prefix network, because it can be implemented very easily in software. The diagram below (trust me, it really _is_ supposed to look like that) is an illustration of how it works. The corresponding lines of program code are shown on the right. The inputs are fed into the network at the top, pass along the connecting lines, are combined by the # operator at various points, and the outputs appear at the bottom.
x1 x2 x3 x4 x5 x6 x7 x8 Input : g, p | | | | | | | | V V V V V V V V | | | | | | | | | | | | | | | | |\ |\ |\ |\ |\ |\ |\ | | \| \| \| \| \| \| \| | # # # # # # # g |= p & (g << 8); | | | | | | | | p &= (p << 8); |\ |\ |\ |\ |\ |\ | | | \: \: \: \: \: \: | | \ \ \ \ \ \ | | :\ :\ :\ :\ :\ :\ | | | \| \| \| \| \| \| | | # # # # # # g |= p & (g << 16); | | | | | | | | p &= (p << 16); |\ |\ |\ |\ | | | | | \: \: \: \: | | | | \ \ \ \ | | | | :\ :\ :\ :\ | | | | | \: \: \: \: | | | | \ \ \ \ | | | | :\ :\ :\ :\ | | | | | \: \: \: \: | | | | \ \ \ \ | | | | ;\ ;\ :\ :\ | | | | | \| \| \| \| | | | | # # # # g |= p & (g << 32); | | | | | | | | | | | | | | | | V V V V V V V V q1 q2 q3 q4 q5 q6 q7 q8 Output : g
To convince yourself this works, select any output qI and trace upwards from the bottom of the diagram. You'll see it leads back to x1, x2, ... , xI, so qI is formed by some computation of x1 # x2 # ... # xI.
[Implementor's note : The 2 program lines that assign to variable p are not strictly correct. By the end of the routine, p1 and p2 have been trashed (reset). However, they are trashed after they can affect the correctness of the routine result.]
Add/Sub versus Attacks
As a comparison three Kogge-Stone routines. A "classical" byte-wise SWAR adder, byte-wise subtraction, and byte-wise rook-attacks in east direction. Note that the inner parallel prefix instructions are the same in all three routines:
gen |= pro & (gen << 1); pro &= (pro << 1); gen |= pro & (gen << 2); pro &= (pro << 2); gen |= pro & (gen << 4);
The difference are the assignments of generator and propagator, and the final result.
Add
The software approach of a Kogge-Stone hardware adder [5] , requires the initial carry bits as generator, thus the intersection of both summands, while the propagator is the modulo 2 sum, the exclusive or of both summands. To avoid inter byte overflows, the propagator has the least significant bits of each byte cleared. However the final carries need one further masked shift and the modulo two sum with the initial propagator.
// SIMD bytewise add a + b
U64 koggeStoneByteAdd(U64 a, U64 b) {
U64 gen, pro;
gen = a & b;
pro = a ^ b;
pro &= ~aFile;
gen |= pro & (gen << 1);
pro &= (pro << 1);
gen |= pro & (gen << 2);
pro &= (pro << 2);
gen |= pro & (gen << 4);
gen =~aFile & (gen << 1);
return gen ^ a ^ b;
}
Sub
Subtraction is based on the two's complement which is ones' complement plus one aka the A-File assuming little-endian rank-file mapping. Thus, it is actually the sum of {a, ~b, one}, which is considered in calculating propagator and generator, which is the majority of all three inputs. Note that
gen =~aFile & (gen << 1); return gen ^ a ^ ~b ^ aFile;
can be re-written like in following routine:
// SIMD bytewise sub a - b
U64 koggeStoneByteSub(U64 a, U64 b) {
U64 gen, pro;
gen = a & ~b; // based on -b = ~b + 1
pro = a ^ ~b;
gen |= aFile & pro; // majority
gen |= pro & (gen << 1);
pro &= (pro << 1);
gen |= pro & (gen << 2);
pro &= (pro << 2);
gen |= pro & (gen << 4);
gen = aFile | (gen << 1);
return gen ^ a ^ ~b;
}
East Attacks
Here the Kogge-Stone algorithm generates the sliding piece attacks along the empty squares. Generator are the rooks or queens, propagator the empty squares without the A-file to avoid wraps.
U64 eastAttacks(U64 occ, U64 rooks) {
U64 gen, pro;
pro = ~occ & ~aFile;
gen = rooks;
gen |= pro & (gen << 1);
pro &= (pro << 1);
gen |= pro & (gen << 2);
pro &= (pro << 2);
gen |= pro & (gen << 4);
gen =~aFile & (gen << 1);
return gen;
}
The mentioned routines also demonstrate, that this east attacking direction may cheaper implemented with Fill by Subtraction based on SWAR-wise techniques and subtracting a rook from a blocking piece:
U64 byteAdd(U64 a, U64 b) {return ((a & ~hFile) + (b & ~hFile)) ^ ((a ^ b) & hFile);}
U64 byteSub(U64 a, U64 b) {return ((a | hFile) - (b & ~hFile)) ^ ((a ^ ~b) & hFile);}
However, due to various left and right shifts, Kogge-Stone can deal with all other seven sliding directions as well.
See also
- Parallel prefix MSB
- SWAR population count of the too slow loop approach
- Flipping and Mirroring
- Pawn Fills
- Occupancy of any Line
- Kogge-Stone Algorithm
Publications
- Peter M. Kogge, Harold S. Stone (1973). A Parallel Algorithm for the Efficient Solution of a General Class of Recurrence Equations. IEEE Transactions on Computers, 1973, C-22, 783-791, pdf
- Richard E. Ladner, Michael J. Fischer (1980). Parallel Prefix Computation. pdf via CiteSeerX
- Clyde Kruskal, Larry Rudolph, Marc Snir (1985). The power of parallel prefix. IEEE Transactions on Computers, Vol. C-34, No. 10
- Peter Sanders, Jesper Larsson Träff (2006). Parallel Prefix (Scan) Algorithms for MPI. in EuroPVM/MPI 2006, LNCS, pdf
- Carl Burch (2009). Introduction to parallel & distributed algorithms. On-line Book
Forum Posts
- flood fill attack bitboards by Steffan Westcott from CCC, September 15, 2002
- Re: Hyperbola Quiesscene: hardly any improvement by Karlo Bala Jr., CCC, January 14, 2009 » Hyperbola Quintessence
External Links
- Hardware algorithms for arithmetic modules from the ARITH research group, Aoki lab., Tohoku University
- Prefix sum from Wikipedia
- parallel prefix computation from National Institute of Standards and Technology
- parallel prefix algorithm from Everything2.com
- Charm++ Tutorial - Parallel Prefix Program
- Joe Zawinul, Trilok Gurtu - Orient Express Part1, YouTube Video
References
- ↑ Carl Burch (2009). Introduction to parallel & distributed algorithms. On-line Book
- ↑ See also
- ↑ Gray Code Conversion from The Aggregate Magic Algorithms by Hank Dietz
- ↑ flood fill attack bitboards by Steffan Westcott from CCC, September 15, 2002
- ↑ Hardware algorithms for arithmetic modules from the ARITH research group, Aoki lab., Tohoku University
