Difference between revisions of "Traversing Subsets of a Set"
GerdIsenberg (talk | contribs) |
GerdIsenberg (talk | contribs) |
||
| Line 174: | Line 174: | ||
* [http://groups.google.com/group/rec.games.chess/msg/f4f0751cc8b928c8 Re: move generators in computer chess, Tricky bit tricks] by [[Marcel van Kervinck]], [[Computer Chess Forums|rgcc]], October 20, 1994 | * [http://groups.google.com/group/rec.games.chess/msg/f4f0751cc8b928c8 Re: move generators in computer chess, Tricky bit tricks] by [[Marcel van Kervinck]], [[Computer Chess Forums|rgcc]], October 20, 1994 | ||
* [http://www.stmintz.com/ccc/index.php?id=490129 Re: algorithm question] by [[Steffan Westcott]], [[CCC]], February 27, 2006 | * [http://www.stmintz.com/ccc/index.php?id=490129 Re: algorithm question] by [[Steffan Westcott]], [[CCC]], February 27, 2006 | ||
| + | * [http://www.talkchess.com/forum3/viewtopic.php?f=7&t=73198 Don't understand CarryRippler] by Marcel Vanthoor, [[CCC]], February 27, 2020 | ||
=External Links= | =External Links= | ||
Revision as of 18:38, 1 March 2020
Home * Programming * Algorithms * Traversing Subsets of a Set
Traversing Subsets of a Set determines the power set of a set, or a subset of the power set with certain properties such as equal cardinality. Represented by a bitboard, this is useful to loop over possible occupancies of a set of rays or lines, and to look for magic factors with a certain cardinality.
Contents
Enumerating All Subsets
All Subsets of the Universal Set
To enumerate all subsets of the universal set -1 is obvious, but takes some time. Assuming one loop cycle takes one nano-second, it would still take 18,446,744,073 seconds or about 585 years!
// enumerate all subsets of the universal set -1
void enumerateAllSubsetsOfTheBitboardUniverse() {
U64 n = 0;
do {
doSomeThingWithSubset(n);
n++;
} while ( n );
}
All Subsets of any Set
// enumerate all subsets of set d
void enumerateAllSubsets(U64 d) {
U64 n = 0;
do {
doSomeThingWithSubset(n);
n = (n - d) & d;
} while ( n );
}
This is how the Carry-Rippler, introduced by Marcel van Kervinck [2] and later by Steffan Westcott [3] works: we first set all "unused" bits of the set by oring the One's Complement of d. The increment ripples a possible carry through all unused bits - and finally we clear all unused bits again by intersection with the set d:
n = ((n | ~d) + 1) & d;
We can safely replace bitwise-or by add, since unused bits are always zero:
n = ((n + ~d) + 1) & d;
Replacing One's Complement by Two's Complement minus one
n = ((n + (-d-1) + 1) & d;
leaves the final expression
n = (n - d) & d;
Subsets with equal Cardinality
Traversing subsets with one bit set was already mentioned in the Bitboard Serialization topic.
Equal cardinality subsets have Same number of one bits - thus Snoob, as synonym of the iterator-function. To use snoob in a loop:
U64 x, y, first = 0x0f; // traverse all 4-bit sequences for (x = first; (y = snoob(x)) > x; x = y) doSomethingWith(y);
We add the LS1B (smallest) to the set, to get a greater number. The former LS1B becomes zero with overflow. If the next higher bit was zero, it takes the carry and the number of set bits didn't change - two flipped bits. Otherwise, if the carry ripples through, leaving further zero(s), we need to set least significant bits accordingly, to keep the cardinality equal. Thus, we xor ripple to get the flipped bits as ones. We shift this sequence right, until it becomes the least significant bits (divide by smallest). To take the two compensating bits off, we need to further divide by 4 (leading or trailing shift right 2). Get the next higher number with the same number of one bits (Snoob) was devised by Bill Gosper as HAKMEM 175 in PDP-6 Assembly [4] and elaborated in Hacker's Delight by Henry S. Warren, Jr. [5] [6].
Snoobing the Universe
// get next greater value with same number of one bits
// Taken from "Hacker's Delight" by Henry S. Warren, Jr.
// originally appeared as HAKMEM ITEM 175 (Bill Gosper)
U64 snoob (U64 x) {
U64 smallest, ripple, ones;
smallest = x & -x;
ripple = x + smallest;
ones = x ^ ripple;
ones = (ones >> 2) / smallest;
return ripple | ones;
}
Modified Snoob
Division by power of two replaced by De Bruijn bitscan and shift right:
const U64 deBruijn = C64(0x03f79d71b4cb0a89);
const unsigned int deBruijnLookup[64] = // or unsigned char
{
0, 1, 48, 2, 57, 49, 28, 3,
61, 58, 50, 42, 38, 29, 17, 4,
62, 55, 59, 36, 53, 51, 43, 22,
45, 39, 33, 30, 24, 18, 12, 5,
63, 47, 56, 27, 60, 41, 37, 16,
54, 35, 52, 21, 44, 32, 23, 11,
46, 26, 40, 15, 34, 20, 31, 10,
25, 14, 19, 9, 13, 8, 7, 6,
};
// get next greater value with same number of one bits
U64 snoob (U64 x) {
U64 smallest, ripple, ones;
smallest = x & (0-x);
ripple = x + smallest;
ones = x ^ ripple;
ones = (ones >> 2) >> deBruijnLookup[(smallest*deBruijn) >> 58];
return ripple | ones;
}
Due to implicit modulo(64) of the shift amount by the processor
(ones >> i) >> 2 == (ones >> 2) >> i might not equal to ones >> (2 + i)!
Reverse Snoob
based on One's Complement:
// get next less value with same number of one bits
U64 rSnoob (U64 sub) {
return ~snoob(~sub);
}
or to safe some bitscans
// get next less value with same number of one bits
U64 rSnoob (U64 sub) {
if ( sub & 1 )
return ~snoob(~sub);
U64 lsb = sub & (0-sub);
return sub ^ lsb ^ (lsb>>1);
}
Snoobing any Sets
combining the Carry Rippler with Snoob - a little more complicated
set: ... 1110 0110 0x..e6 e.g. all subsets with two set bits: ... 0000 0110 0x..06 ... 0010 0010 0x..22 ... 0010 0100 0x..24 ... 0100 0010 0x..42 ... 0100 0100 0x..44 ... 0110 0000 0x..60 ... 1000 0010 0x..82 ... 1000 0100 0x..84 ... 1010 0000 0x..a0 ... 1100 0000 0x..c0
// get next greater subset of set with same number of one bits
U64 snoob (U64 sub, U64 set) {
U64 tmp = sub-1;
U64 rip = set & (tmp + (sub & (0-sub)) - set);
for(sub = (tmp & sub) ^ rip; sub &= sub-1; rip ^= tmp, set ^= tmp)
tmp = set & (0-set);
return rip;
}
// get next less set of a subset with same number of one bits
U64 rSnoob (U64 sub, U64 set) {
return ~snoob(~sub & set, set) & set;
}
See also
Selected Publications
- Michael Beeler, Bill Gosper, Rich Schroeppel (1972). HAKMEM, Memo 239. CSAIL, MIT, ITEM 175 (Gosper)
- Frank Ruskey (2003). Combinatorial Generation. University of Victoria, pdf
- Henry S. Warren, Jr. (2012). Hacker's Delight, 2nd Edition. Addison-Wesley
Forum Posts
- Re: move generators in computer chess, Tricky bit tricks by Marcel van Kervinck, rgcc, October 20, 1994
- Re: algorithm question by Steffan Westcott, CCC, February 27, 2006
- Don't understand CarryRippler by Marcel Vanthoor, CCC, February 27, 2020
External Links
- Partially ordered set from Wikipedia
- Power set from Wikipedia
- Led Zeppelin - Dazed and Confused, YouTube Video, Lost Performances (2/5)
References
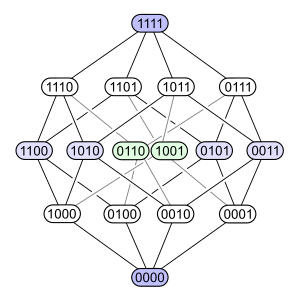
- ↑ The 4D-hypercube, layered according to distance from one corner. As described in "Alice in Wonderland" by the Cheshire Cat, this vertex-first-shadow of the tesseract forms a rhombic dodecahedron. Note that the two central (green) vertices should coincide if using an orthogonal projection from 4 to 3 dimensions, but were drawn here slightly apart. The eight nibbles with odd binary digit sums form a cube and are marked in white. The two palindromes 0110 and 1001 (compare XOR and XNOR) are projected in the center of the rhombic dodecahedron and are marked in green. The other six nibbles with even binary digit sums form an octahedron and are marked in blue, image by Lipedia, 2010, Hasse diagram from Wikipedia
- ↑ Tricky bit tricks by Marcel van Kervinck, rec.games.chess, October 20, 1994
- ↑ Re: algorithm question by Steffan Westcott, CCC, February 27, 2006
- ↑ Michael Beeler, Bill Gosper, Rich Schroeppel (1972). HAKMEM, Memo 239. CSAIL, MIT
- ↑ Sample section of Hacker's Delight, Chapter 2 Basics (pdf) by Henry S. Warren, Jr. pp.14 Figure 2–1. Next higher number with same number of 1-bits.
- ↑ C code for most of the programs that appear in HD | Fig. 2-1. Next higher number with same number of 1-bits