Anti-Diagonals
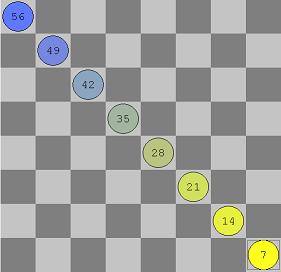
Anti-Diagonals are the diagonals from south-east to north-west on a chess board, the main anti-diagonal is h1\a8. There are 15 anti-diagonals, with line-length from 1 to 8. An Anti-Diagonal is monochrome, all their squares are either white or black.
Contents
Square Mapping Notes
A 90 degree rotation of the Chessboard, as well as flipping vertically (reversed ranks) or (exclusive) mirroring horizontally (reversed files), change the roles of diagonals and anti-diagonals. However, we define the main diagonal on the chess board from a1/h8 and the main anti-diagonal from h1\a8. Whether the square difference of neighbored squares on a diagonal or anti-diagonal is either 7 or 9, depends on the square mapping. We further rely on little-endian rank-file mapping.
Square Difference
Within a 0..63 square index range and the mentioned square mapping (a1 = 0), the difference of two neighbored squares (if any) on an anti-diagonal is seven.
Enumeration
If we follow an anti-diagonal from south-east (h1) to north-west (a8) step by step, we increment the rank, but decrement the file, which yields in same sum. Thus, adding rank and file indices enumerates all Anti-Diagonals.
- Square a1 (file- and rank index 0) is therefor anti-diagonal with index 0 and length 1.
- The main anti-diagonal h1\a8 with index 7 and length 8.
- Square h8 is the 15th anti-diagonal with index 14 and length 1.
- All even indices are the anti-diagonals with dark squares
rank + file
| r/f | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Alternative Enumeration
Some alternative enumeration of anti-diagonals to make the main-diagonal index 0, by xoring the sum with 7 (which complements the lower three bits of the sum). This yields in a 0..15 range with 8 as gap or Nexus in the center of the range:
(rank + file) ^ 7
| r/f | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 7 | 0 | 15 | 14 | 13 | 12 | 11 | 10 | 9 |
| 6 | 1 | 0 | 15 | 14 | 13 | 12 | 11 | 10 |
| 5 | 2 | 1 | 0 | 15 | 14 | 13 | 12 | 11 |
| 4 | 3 | 2 | 1 | 0 | 15 | 14 | 13 | 12 |
| 3 | 4 | 3 | 2 | 1 | 0 | 15 | 14 | 13 |
| 2 | 5 | 4 | 3 | 2 | 1 | 0 | 15 | 14 |
| 1 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 15 |
| 0 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Two Squares on a Anti-Diagonal
Two Squares are on the same Anti-Diagonal, if sum of file and rank distance is zero
bool squaresOnSameAntiDiagonal(int sq1, int sq2) {
return ((sq2 - sq1) & 7) + ((sq2>>3) - (sq1>>3)) == 0;
}
The alternative approach, to test whether the square difference is divisible by 7, would take extra conditions, since the outer squares of the main-diagonal (63-0) would wrongly classified otherwise [2]
See also
External Links
References
- ↑ Bibob image by Gerd Isenberg
- ↑ An undetected bug for 10 years by Oliver Brausch, CCC, August 18, 2020