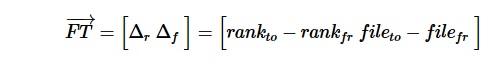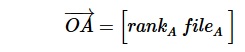Vector Attacks
Home * Board Representation * Mailbox * Vector Attacks

Vector Attacks [2],
the application of vectors in the Chebyshev vector space of a chessboard to the problem of chess attacks, including static exchange evaluation (SEE), and testing whether moves are pseudo-legal.
Displacement and Position Vectors
A displacement vector is a tuple of rank- and file-difference of two squares, for instance from and to square of a move.
The position vector of square A is the displacement to an arbitrary reference origin O.
Vector Boards
Vector board arrays with a one-dimensional, scalar index, require the difference of any two mailbox square indices preserve their rank- and file-difference and therefore their direction and distance relationship, which implies using the number of file differences as array dimension - which is 15 rather than 8 for the number of files. Therefore, the 8x8 mailbox needs at least 7 padded columns (files) of a 15xNROWS (or 16xNROWS) vector array:
or
Vector as Index
Represented as such a square difference, displacement vectors can be used to index 225 (15x15) or 240 (16x15) sized lookup tables for stuff dependent on square relations, that is Chebyshev distance, Manhattan-distance, boolean ray properties and most importantly, increment vectors along a ray, or in the world of bitboards, rotated in-between sets. Thus, the up to fourfold board size of the vector boards, largely pays off, since pure 8x8 coordinates would require two-dimensional butterfly tables of size 4096 indexed by two square indices for the same purpose. To keep indices positive, an offset of 112 respective 119 (120) is added.
Superimposed Lookup
8x8 tables inside 15x15 tables were already proposed by Mikhail Botvinnik as used in Pioneer [3]. The table below demonstrates the vector enumeration from a square (here c2) on a 8x8 board, superimposed on the 15x15 array in such a way that the from square (c2) coincides with the central square of the 15x15 array, which is the origin, tail, or base of all displacement vectors.
╔════╤════╤════╤════╤════╤════╤════╤════╤════╤════╤════╤════╤════╤════╤════╗
210 ║ 98| 99 | 100| 101| 102| 103| 104| 105| 106| 107| 108| 109| 110| 111| 112║
╟────┼────┼────┼────┼────╔════╤════╤════╤════╤════╤════╤════╤════╗────┼────╢
195 ║ 83| 84| 85| 86| 87║ 88| 89| 90| 91| 92| 93| 94| 95║ 96| 97║
╟────┼────┼────┼────┼────╟────┼────┼────┼────┼────┼────┼────┼────╢────┼────╢
180 ║ 68| 69| 70| 71| 72║ 73| 74| 75| 76| 77| 78| 79| 80║ 81| 82║
╟────┼────┼────┼────┼────╟────┼────┼────┼────┼────┼────┼────┼────╢────┼────╢
165 ║ 53| 54| 55| 56| 57║ 58| 59| 60| 61| 62| 63| 64| 65║ 66| 67║
╟────┼────┼────┼────┼────╟────┼────┼────┼────┼────┼────┼────┼────╢────┼────╢
150 ║ 38| 39| 40| 41| 42║ 42| 44| 45| 46| 47| 48| 49| 50║ 51| 52║
╟────┼────┼────┼────┼────╟────┼────┼────┼────┼────┼────┼────┼────╢────┼────╢
135 ║ 23| 24| 25| 26| 27║ 28| 29| 30| 31| 32| 33| 34| 35║ 36| 37║
╟────┼────┼────┼────┼────╟────┼────┼────┼────┼────┼────┼────┼────╢────┼────╢
120 ║ 8| 9| 10| 11| 12║ 13| 14| 15| 16| 17| 18| 19| 20║ 21| 22║
╟────┼────┼────┼────┼────╟────┼────╔════╗────┼────┼────┼────┼────╢────┼────╢
105 ║ -7| -6| -5| -4| -3║ -2| -1║ 0║ 1| 2| 3| 4| 5║ 6| 7║
╟────┼────┼────┼────┼────╟────┼────╚════╝────┼────┼────┼────┼────╢────┼────╢
90 ║ -22| -21| -20| -19| -18║ -17| -16| -15| -14| -13| -12| -11| -10║ -9| -8║
╟────┼────┼────┼────┼────╚════╧════╧════╧════╧════╧════╧════╧════╝────┼────╢
75 ║ -37| -36| -35| -34| -33| -32| -31| -30| -29| -28| -27| -26| -25| -24| -23║
╟────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────╢
60 ║ -52| -51| -50| -49| -48| -47| -46| -45| -44| -43| -42| -41| -40| -39| -38║
╟────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────╢
45 ║ -67| -66| -65| -64| -63| -62| -61| -60| -59| -58| -57| -56| -55| -54| -53║
╟────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────╢
30 ║ -82| -81| -80| -79| -78| -77| -76| -75| -74| -73| -72| -71| -70| -66| -68║
╟────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────╢
15 ║ -97| -96| -95| -94| -93| -92| -91| -90| -89| -88| -87| -86| -85| -84| -83║
╟────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────╢
0 ║-112|-111|-110|-109|-108|-107|-106|-105|-104|-103|-102|-101|-100| -99| -98║
╚════╧════╧════╧════╧════╧════╧════╧════╧════╧════╧════╧════╧════╧════╧════╝
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Ray Vectors
Ray vectors are unit vectors to eight neighboring squares, scaled by Chebyshev distance. In the domain of sliding piece attacks, unit vectors act as increment vectors if none zero, to determine squares in-between are empty, and a target square is attacked by a sliding piece on its origin. Following table demonstrates the queen unit or increment vectors, superimposed on the 15x15 array in such a way that the queen square (here c2) coincides with the central square of the 15x15 array.
char rayUnitVectorQueen[15*15];
╔════╤════╤════╤════╤════╤════╤════╤════╤════╤════╤════╤════╤════╤════╤════╗
210 ║ 14| | | | | | | 15| | | | | | | 16║
╟────┼────┼────┼────┼────╔════╤════╤════╤════╤════╤════╤════╤════╗────┼────╢
195 ║ | 14| | | ║ | | 15| | | | | ║ 16| ║
╟────┼────┼────┼────┼────╟────┼────┼────┼────┼────┼────┼────┼────╢────┼────╢
180 ║ | | 14| | ║ | | 15| | | | | 16║ | ║
╟────┼────┼────┼────┼────╟────┼────┼────┼────┼────┼────┼────┼────╢────┼────╢
165 ║ | | | 14| ║ | | 15| | | | 16| ║ | ║
╟────┼────┼────┼────┼────╟────┼────┼────┼────┼────┼────┼────┼────╢────┼────╢
150 ║ | | | | 14║ | | 15| | | 16| | ║ | ║
╟────┼────┼────┼────┼────╟────┼────┼────┼────┼────┼────┼────┼────╢────┼────╢
135 ║ | | | | ║ 14| | 15| | 16| | | ║ | ║
╟────┼────┼────┼────┼────╟────┼────┼────┼────┼────┼────┼────┼────╢────┼────╢
120 ║ | | | | ║ | 14| 15| 16| | | | ║ | ║
╟────┼────┼────┼────┼────╟────┼────╔════╗────┼────┼────┼────┼────╢────┼────╢
105 ║ -1| -1| -1| -1| -1║ -1| -1║ Q ║ 1| 1| 1| 1| 1║ 1| 1║
╟────┼────┼────┼────┼────╟────┼────╚════╝────┼────┼────┼────┼────╢────┼────╢
90 ║ | | | | ║ | -16| -15| -14| | | | ║ | ║
╟────┼────┼────┼────┼────╚════╧════╧════╧════╧════╧════╧════╧════╝────┼────╢
75 ║ | | | | | -16| | -15| | -14| | | | | ║
╟────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────╢
60 ║ | | | | -16| | | -15| | | -14| | | | ║
╟────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────╢
45 ║ | | | -16| | | | -15| | | | -14| | | ║
╟────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────╢
30 ║ | | -16| | | | | -15| | | | | -14| | ║
╟────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────╢
15 ║ | -16| | | | | | -15| | | | | | -14| ║
╟────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────┼────╢
0 ║ -16| | | | | | | -15| | | | | | | -14║
╚════╧════╧════╧════╧════╧════╧════╧════╧════╧════╧════╧════╧════╧════╧════╝
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Increment Vectors
During offset move generation, each piece applies a specific displacement or increment vector (offset) for each move direction, added to the position vector of the origin square to determine the next potential move target in that direction, sliding pieces continuing in the same direction as long the targets are empty. Due to the additional padded files and possibly ranks, off the board test are as simple as the 10x12 board with surrounding files and ranks containing off the board codes as sentinel values. The 0x88 approach, a special 16x8 implementation of Vector Attacks, already indicates outside squares by its upper nibble bits masked by 0x88.
One may argue, the 0x88 test is cheaper for off the board tests, because it does not need to lookup if the 0x88 test is true. On the other hand, for most cases, if false, it needs a lookup anyway, to perform a second test whether the square is empty, or occupied by an own or opponent piece [4] [5].
New Architecture
Vector Attacks based on a 15x12 board were topic of Fritz Reul's Ph.D. thesis New Architectures in Computer Chess, code samples given from Reul's Loop Leiden engine [6].
Source-Destination
In conjunction with disjoint piece flags and piece-lists, Vector Attacks allow efficient move generation of sliding pieces, even for quiescence search with a leading blocker loop:
increment = rayVector[direction];
for (tosq = fromsq + increment; board[tosq] == EMPTY; tosq += increment);
if ( isOpponentPiece (board[tosq]) )
{
/* generate capture */
}
Destination-Source
A destination-source blocker loop, to test whether a sliding piece on a from square attacks a target square, uses the reversed ray direction in order to dispense with additional conditions:
increment = rayUnitVectorQueen[15*15/2 + fromsq - tosq];
if ( increment ) {
for (sq = tosq + increment; board[sq] == EMPTY; sq += increment);
if ( sq == fromsq ) {
/* a queen on fromsq attacks tosq */
}
}
Implementations
0x88
see main article 0x88
The 0x88 or 16x8 board uses nibbles for both rank and file coordinates inside a byte, and utilizes the redundant upper bit to indicate invalid squares outside the board, usually then not used as index.
Layout
--------XXXXXXXX --------XXXXXXXX --------XXXXXXXX --------XXXXXXXX --------XXXXXXXX --------XXXXXXXX --------XXXXXXXX --------XXXXXXXX
Coordinate Transformation
16x8 square coordinate by file and rank and vice versa:
sq0x88 = 16 * rank07 + file07; file07 = sq0x88 & 7; rank07 = sq0x88 >> 4; // sq0x88 / 16
0x88 index by a 0..63 square index needs to add the three upper rank bits:
sq0x88 = sq + (sq & ~7);
15x12
The odd number of files makes the square color only dependent from the least significant index bit. Usually the seven surrounding border files are divided 4:3 (Offset 34) or 3:4 (Offset 33). One may also use 15x15 for a symmetric treatment of files and ranks as proposed by Fritz Reul [7] .
Layout
XXXXXXXXXXXXXXX XXXXXXXXXXXXXXX XXXX--------XXX XXXX--------XXX XXXX--------XXX XXXX--------XXX XXXX--------XXX XXXX--------XXX XXXX--------XXX XXXX--------XXX XXXXXXXXXXXXXXX XXXXXXXXXXXXXXX
Coordinate Transformation
Coordinate transformation is usually not needed while generating moves, since piece-lists, increments and move coordinates are only based on 15x12 coordinates. Anyway, for the sake of completeness valid 15x12 square transformation to file and rank indices and vice versa might be done quite efficiently without any x86 div and mul instructions, but load effective address (lea) - otherwise simple lookup tables may used to convert coordinates:
sq15x12 = 15 * rank07 + file07 + 34; rank07 = ((sq15x12 - 34) * 9) >> 7; // div by reciprocal mul file07 = sq15x12 - 34 - 15 * rank07; // % 15
16x12
Usually the eight surrounding border files are divided 4:4, so the offset of the upper left square is 36. For a symmetric treatment of files and ranks, 16x16 is also quite common [8] .
Layout
XXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXX XXXX--------XXXX XXXX--------XXXX XXXX--------XXXX XXXX--------XXXX XXXX--------XXXX XXXX--------XXXX XXXX--------XXXX XXXX--------XXXX XXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXX
Coordinate Transformation
16x12 square coordinate by file and rank and vice versa:
sq16x12 = 16 * rank07 + file07 + 36; rank07 = (sq16x12 - 36) >> 4; // div 16 file07 = (sq16x12 - 36) & 7; // % 8
16x12 square index by a 0..63 square index needs to add the three upper rank bits plus offset:
sq16x12 = sq8x8 + (sq8x8 & ~7) + 36;
Convert 16x12 square index to 0..63 square index:
file8x8 = (sq16x12 & 0xf) - 4 rank8x8 = ((sq16x12 >> 4) - 2 sq8x8 = (((sq16x12 >> 4) - 2) << 3) + (sq16x12 & 0xf) - 4;
Conclusion
A combination of 0x88 and 10x12 Board with surrounded ranks, that is 16x12 or even 16x16 for a symmetric treatment of files and ranks (or 15x12, 15x15) seems slightly more efficient than pure 0x88 aka 16x8, making the "off the board" index condition almost redundant, since it can be combined with the coding of the guard or sentinal squares [9] [10] [11] [12] .
See also
- 0x88
- 0x88 meets Bitboards
- 10x12 Board
- 8x8 Board
- Distance
- Direction
- Intersection Squares as application of 0x88 coordinates
- Sliding Piece Attacks with Bitboards
Publications
- Mikhail Botvinnik (1968). Algoritm igry v shakhmaty. (The algorithm of chess)
- Mikhail Botvinnik (1970). Computers, Chess and Long-Range Planning. Springer
- Paul Wiereyn (1985). Inventive Problem Solving. ICCA Journal, Vol. 8, No. 4
- Boris Stilman (1994). A Linguistic Geometry of the Chess Model. Advances in Computer Chess 7, pdf draft
- Fritz Reul (2009). New Architectures in Computer Chess. Ph.D. Thesis, Chapter 2 Non-Bitboard Architectures
Forum Posts
2000 ...
- Question:1.hashtable 2.board 3.C by Teerapong Tovirat, CCC, June 13, 2000
- Re: Question:1.hashtable 2.board 3.C by Christophe Théron, CCC, June 13, 2000
- Re: Question:1.hashtable 2.board 3.C by Eugene Nalimov, CCC, June 13, 2000
- 0x88 is not so smart by Christophe Théron, CCC, June 13, 2000 » 0x88
- Fastest Conversion from 0x88 board to 8x8 board representation by Artem Pyatakov, CCC, July 06, 2001
- Re: Fruit's Board Representation? by Fabien Letouzey, Winboard Forum, April 28, 2005 » Fruit
2010 ...
- GetSmallestAttacker() in 16x12 board representation by metax, CCC, January 17, 2010 » Static Exchange Evaluation, Piece-Lists
- Recommended board representation for a rookie by Fred Hamilton, CCC, November 26, 2016
- Re: Recommended board representation for a rookie by Harm Geert Muller, CCC, November 26, 2016
- What're advantages of board 16x12? by Nguyen Pham, CCC, December 30, 2016
External Links
- Vector (mathematics and physics) from Wikipedia
- Euclidean vector from Wikipedia
- Position (vector) from Wikipedia
- Displacement (vector) from Wikipedia
- Linear algebra from Wikipedia
- Vector space from Wikipedia
- The Dave Pike Set - Attack Of The Green Misers, Infra-Red (1970), YouTube Video
- lineup: Dave Pike, Volker Kriegel, Hans Rettenbacher, Peter Baumeister
References
- ↑ A vector in the Cartesian plane, showing the position of a point A with coordinates (2,3), Euclidean vector from Wikipedia
- ↑ Re: Fruit's Board Representation? by Fabien Letouzey, Winboard Forum, April 28, 2005
- ↑ Boris Stilman (1994). A Linguistic Geometry of the Chess Model. Advances in Computer Chess 7, pdf draft
- ↑ Re: Question:1.hashtable 2.board 3.C by Christophe Théron, CCC, June 13, 2000
- ↑ 0x88 is not so smart by Christophe Théron, CCC, June 13, 2000
- ↑ Fritz Reul (2009). New Architectures in Computer Chess. Ph.D. Thesis, Chapter 2 Non-Bitboard Architectures
- ↑ Fritz Reul (2009). New Architectures in Computer Chess. Ph.D. Thesis, Chapter 2 Non-Bitboard Architectures
- ↑ Re: Fruit's Board Representation? by Fabien Letouzey, Winboard Forum, April 28, 2005
- ↑ Re: Question:1.hashtable 2.board 3.C by Christophe Théron, CCC, June 13, 2000
- ↑ Re: Fruit's Board Representation? by Fabien Letouzey, Winboard Forum, April 28, 2005
- ↑ Fritz Reul (2009). New Architectures in Computer Chess. Ph.D. Thesis, 2.2.1 Computer Chessboard Representation
- ↑ Re: Recommended board representation for a rookie by Harm Geert Muller, CCC, November 26, 2016