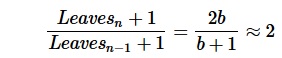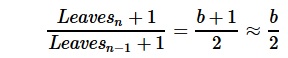Odd-Even Effect
Home * Search * Alpha-Beta * Odd-Even Effect
The Odd-Even Effect of Alpha-Beta is caused by the topology of the minimal game tree of uniform depth n and branching factor b. Michael Levin found the formula of the number of leaf nodes, which was published in Edwards' and Hart's 1961 Alpha-Beta paper [2] .
Even Leaves
2bn/2 - 1
Odd Leaves
b(n+1)/2 + b(n-1)/2 - 1
Node Types
Number of Leaf nodes of a certain Node type at depth n [3]:
n = even:
PVn = 1 CUTn = bn/2 - 1 = CUTn-1 ALLn = bn/2 - 1 = ALLn-1 + bn/2 - b(n-2)/2
n = odd:
PVn = 1 CUTn = b(n+1)/2 - 1 = CUTn-1 + b(n+1)/2 + b(n-1)/2 ALLn = b(n-1)/2 - 1 = ALLn-1
So for the sum of the Leaf-nodes at depth n as well as the total sum of nodes (including interior nodes) up to depth n holds
ALLn = CUTn-1
Leaves by Depth
Assuming a constant branching factor of 40, this results in following number of leaves, using the floor and ceiling formulas :
CUTn = b⌈n/2⌉ - 1 ALLn = b⌊n/2⌋ - 1
| depth | worst case | best case | PV | CUT | ALL |
|---|---|---|---|---|---|
| n | bn | b⌈n/2⌉ + b⌊n/2⌋ - 1 | 1 | b⌈n/2⌉ - 1 | b⌊n/2⌋ - 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 40 | 40 | 1 | 39 | 0 |
| 2 | 1,600 | 79 | 1 | 39 | 39 |
| 3 | 64,000 | 1,639 | 1 | 1,599 | 39 |
| 4 | 2,560,000 | 3,199 | 1 | 1,599 | 1,599 |
| 5 | 102,400,000 | 65,569 | 1 | 63,999 | 1,599 |
| 6 | 4,096,000,000 | 127,999 | 1 | 63,999 | 63,999 |
| 7 | 163,840,000,000 | 2,623,999 | 1 | 2,559,999 | 63,999 |
| 8 | 6,553,600,000,000 | 5,119,999 | 1 | 2,559,999 | 2,559,999 |
resulting in following
Leaf Ratios
Iterative Deepening
Inside an iterative deepening framework, the odd-even effect causes an asymmetry in time usage. Even-odd transitions grow (much) more than odd-even. The effect diminishes due to quiescence search and selectivity in the upper part of the tree. However, past and recent programs addressed that issue. For instance L'Excentrique used two ply increments [4], and Bebe had no quiescence at all, and searched in two ply increments as well [5]. Other programs used fractional plies for extensions [6] and ID increments.
Score Oscillation
Additionally, many programs exhibit an effect on the score based on the parity of the search depth due to the extra tempo of odd ply searches. Scores are stable when one looks at results from the odd plies only, or even plies only, but are sometimes unstable when they are mixed. One remedial on this odd-even effect is to apply a tempo bonus in leaf evaluation for the side to move.
See also
Forum Posts
- Odd ply versus even ply searches by Robert Hyatt, rgcc, February 28, 1996 » Bebe
- PROG: odd/even score alternance by Rémi Coulom, rgcc, June 5, 1997 » Tempo
- pv score oscillation by Willie Wood, CCC, October 18, 1997
- Node counts at a given depth/iteration in search by BB+, OpenChess Forum, May 23, 2011
- CUT/ALL nodes ratio by Daniel Shawul, CCC, June 06, 2013
- Asymmetrical evaluation by Laurie Tunnicliffe, CCC, May 24, 2016 » Asymmetric Evaluation
External Links
References
- ↑ Image by TNSENesamaniTpr, July 06, 2017, Wikimedia Commons
- ↑ Daniel Edwards, Timothy Hart, (1961). The Alpha-Beta Heuristic. AIM-030, available from DSpace at MIT
- ↑ CUT/ALL nodes ratio by Daniel Shawul, CCC, June 06, 2013
- ↑ Eric Thé (1992). An analysis of move ordering on the efficiency of alpha-beta search. Master's thesis, McGill University, advisor Monroe Newborn
- ↑ Odd ply versus even ply searches by Robert Hyatt, rgcc, February 28, 1996
- ↑ David Levy, David Broughton, and Mark Taylor (1989). The SEX Algorithm in Computer Chess. ICCA Journal, Vol. 12, No. 1