Node Types
Home * Search * Node * Node Types
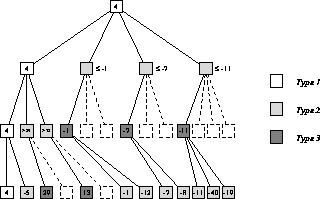
Node Types are classifications of nodes as expected inside a minimal alpha-beta tree, or as determined by the search. These types were first formulated by Donald Knuth and Ronald Moore when describing the alpha-beta algorithm [2] and further analyzed by Judea Pearl [3]. While Knuth used the terms Type 1, 2, and 3, Tony Marsland and Fred Popowich introduced the more descriptive terms PV-, Cut- and All-nodes [4] [5].
Node types as established by the search are stored inside the transposition table, indicating whether the score is either exact, lower or upper bounded. Expected node types, as determined by tree topology, probing the transposition table, or comparing scores of a static evaluation considering threats, or even a reduced search or quiescence search, with the bounds, may be considered by various (parallel) search algorithms and in decisions concerning selectivity.
PV-Nodes
PV-nodes (Knuth's Type 1) are nodes that have a score that ends up being inside the window. So if the bounds passed are [a,b], with the score returned s, a<s<b. These nodes have all moves searched, and the value returned is exact (i.e., not a bound), which propagates up to the root along with a principal variation.
- Root Node and the Leftmost Nodes are always PV-nodes
- In Principal Variation Search, PV-nodes are defined by beta-alpha>1
- All Siblings of a PV-node are expected Cut-nodes
Cut-Nodes
Cut-nodes (Knuth's Type 2), otherwise known as fail-high nodes, are nodes in which a beta-cutoff was performed. So with bounds [a,b], s>=b. A minimum of one move at a Cut-node needs to be searched. The score returned is a lower bound (might be greater) on the exact score of the node
- In Principal Variation Search Cut-nodes are searched with null windows
- The child of a Cut-node is an All-node
- The parent of a Cut-node is either a PV- or All-node
- The ply distance of a Cut-node to its PV-ancestor is odd
All-Nodes
All-nodes (Knuth's Type 3), otherwise known as fail-low nodes, are nodes in which no move's score exceeded alpha. With bounds [a,b], s<=a. Every move at an All-node is searched, and the score returned is an upper bound, the exact score might be less.
- In Principal Variation Search All-nodes are searched with null windows
- The children of an All-node are Cut-nodes
- The parent of an All-node is a Cut-node
- The ply distance of an All-node to its PV-ancestor is even
Node Types in PVS
Onno
Onno by Onno Garms determines expected node types, beside other things, to perform IID not only at PV-nodes but also at expected Cut-nodes. Onno Garms gave the following rules [6]
- The root node is a PV-node
- The first child of a PV-node is a PV-node
- The further children are searched by a scout search as CUT-nodes
- PVS re-search is done as PV-node
- The first node of bad pruning is a CUT-node
- The node after a null move is a CUT-node
- The first node of null move verification is a CUT-node
- Internal iterative deepening does not change the node type
- The first child of a CUT-node is an ALL-node
- Further children of a CUT-node are CUT-nodes
- Children of ALL-nodes are CUT-nodes
Summary
Following summary was given by Pradu Kannan similar to Onno's definition as an attempt to predict the node type before searching the node by assuming reasonably good move ordering on PV-nodes and Cut-nodes [7]:
- The root node is a PV-node
- The first child of a PV-node is a PV-node
- Children of PV-nodes that are searched with a zero-window scout search are Cut-nodes
- Children of PV-nodes that have to be re-searched because the scout search failed high, are PV-nodes
- The first child of a Cut-node, and other candidate cutoff moves (nullmove, killers, captures, checks, ...) is an All-node
- A Cut-node becomes an All-node once the first and all candidate cutoff moves are searched
- Children of All-nodes are Cut-nodes
Number of Leaf Nodes
Formulas
As emphasized by Daniel Shawul [8], the formulas for the number of leaf nodes of a certain Node type with uniform depth n and branching factor b, using floor and ceiling of n/2 (cut the ceiling, all the floor) ...
PV = 1 CUT = b⌈n/2⌉ - 1 ALL = b⌊n/2⌋ - 1
... are already the subexpressions ...
L = PV + CUT + ALL
... in Levin's famous formula demonstrating the odd-even effect of alpha-beta
L = b⌈n/2⌉ + b⌊n/2⌋ - 1
Table
Assuming a constant branching factor of 40, this results in following number of leaves:
| depth | worst case | best case | PV | CUT | ALL |
|---|---|---|---|---|---|
| n | bn | b⌈n/2⌉ + b⌊n/2⌋ - 1 | 1 | b⌈n/2⌉ - 1 | b⌊n/2⌋ - 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 40 | 40 | 1 | 39 | 0 |
| 2 | 1,600 | 79 | 1 | 39 | 39 |
| 3 | 64,000 | 1,639 | 1 | 1,599 | 39 |
| 4 | 2,560,000 | 3,199 | 1 | 1,599 | 1,599 |
| 5 | 102,400,000 | 65,569 | 1 | 63,999 | 1,599 |
| 6 | 4,096,000,000 | 127,999 | 1 | 63,999 | 63,999 |
| 7 | 163,840,000,000 | 2,623,999 | 1 | 2,559,999 | 63,999 |
| 8 | 6,553,600,000,000 | 5,119,999 | 1 | 2,559,999 | 2,559,999 |
Quotes
Robert Hyatt on the distinction between ALL- and CUT-nodes [9]:
In CB, I used this extensively, because you never want to split at a CUT node, and want to prefer an ALL node. YBW tries to recognize an ALL node by requiring that at least one move be searched before splitting, since > 90% of CUT nodes are discovered on the first move searched. But waiting on that first move introduces some wait time, and if you knew it was an ALL node from the get-go, you could split before the first move is completed. That was the basic premise behind the iterated search and DTS algorithm in Cray Blitz ...
See also
Selected Publications
- Donald Knuth, Ronald W. Moore (1975). An analysis of alpha-beta pruning. Artificial Intelligence, Vol. 6, No. 4, pp 293–326. Reprinted in Donald Knuth (2000). Selected Papers on Analysis of Algorithms. CSLI lecture notes series 102, ISBN 1-57586-212-3
- Igor Roizen (1981). On the Average Number of Terminal Nodes examined by Alpha-Beta. Technical Report UCLA-ENG-CSL-8108, University of California at Los Angeles, Cognitive Systems Laboratory
- Judea Pearl (1982). The Solution for the Branching Factor of the Alpha-Beta Pruning Algorithm and its Optimality. Communications of the ACM, Vol. 25, No. 8, pp. 559-564
- Tony Marsland, Fred Popowich (1985). Parallel Game-Tree Search. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 7, No. 4, pp. 442-452. 1984 pdf (Draft)
- Mark Winands, Jaap van den Herik, Jos Uiterwijk, Erik van der Werf (2003). Enhanced forward pruning. pdf » Enhanced Forward Pruning
Forum Posts
2000 ...
- ALL node definition by Alvaro Cardoso, CCC, February 21, 2003
- Fruit - Question for Fabien by Dan Honeycutt, CCC, March 11, 2004 » Fruit, Transposition Table, Principal Variation, Principal Variation Search
- Re: Fruit - Question for Fabien by Fabien Letouzey, CCC, March 11, 2004
- Re: Attack table by Zach Wegner, Winboard Forum, October 22, 2004 » Attack and Defend Maps
2005 ...
- Move ordering at different (Knuth) node types by Tom Likens, Winboard Forum, February 21, 2006 » Move Ordering
- PV based decisions by Mark Lefler, Winboard Forum, April 27, 2006
- NMP on ALL nodes by Onno Garms, Winboard Forum, April 15, 2007 » Null Move Pruning
- Slight enhancement to PVS by Pradu Kannan, Winboard Forum, June 10, 2007
- Nodes type clarification by Mathieu Pagé, CCC, October 05, 2008
- Different handling of ALL / CUT nodes by Gregory Strong, CCC, March 22, 2009
2010 ...
- CUT" vs "ALL" nodes by Larry Kaufman, CCC, March 7, 2011
- On internal iterative deepening by Onno Garms, CCC, March 13, 2011 » Internal Iterative Deepening, Onno
- When does a cut-node became an all-node? by Alcides Schulz, CCC, March 27, 2012
- Question about PVS and nodes type by Patrice Duhamel, CCC, May 28, 2013 » Principal Variation Search
- CUT/ALL nodes ratio by Daniel Shawul, CCC, June 06, 2013
- LMR at CUT nodes can be arbitrarily bad! by Michel Van den Bergh, CCC, June 20, 2013 » Late Move Reductions, Python
- Pruning in PV nodes by Sergei S. Markoff, CCC, January 14, 2014 » Reductions, Root
- Node Types and Thoughts On Their Application by Cheney Nattress, CCC, February 26, 2014
- Null move pruning on PV nodes by Eric Oldre, CCC, July 22, 2014 » Null Move Pruning
- LMP in PV nodes by Peter Österlund, CCC, December 27, 2014 » Move Count Based Pruning, Texel
2015 ...
- Recognizing PV nodes by Martin Fierz, CCC, March 29, 2016
- What is wrong with doing Nulls & ttcuts in a pv node ? by Mahmoud Uthman, CCC, January 21, 2017 » Null Move Pruning, PV-Nodes, Transposition Table
- cut nodes by Folkert van Heusden, CCC, October 18, 2017 » Cut-Nodes
- Pruning at PV nodes? by Mahmoud Uthman, CCC, January 06, 2019 » Pruning, PV-Nodes
External Links
- Analysis of Alpha-Beta Pruning from the Parallel Computing Works ebook
References
- ↑ Analysis of Alpha-Beta Pruning from the Parallel Computing Works ebook
- ↑ Donald Knuth, Ronald W. Moore (1975). An analysis of alpha-beta pruning. Artificial Intelligence, Vol. 6, No. 4, pp 293–326. Reprinted in Donald Knuth (2000). Selected Papers on Analysis of Algorithms. CSLI lecture notes series 102, ISBN 1-57586-212-3
- ↑ Judea Pearl (1982). The Solution for the Branching Factor of the Alpha-Beta Pruning Algorithm and its Optimality. Communications of the ACM, Vol. 25, No. 8, pp. 559-564
- ↑ Mark Winands, Jaap van den Herik, Jos Uiterwijk, Erik van der Werf (2003). Enhanced forward pruning. pdf
- ↑ Tony Marsland, Fred Popowich (1985). Parallel Game-Tree Search. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 7, No. 4, pp. 442-452. 1984 pdf (Draft)
- ↑ Re: On internal iterative deeping by Onno Garms, CCC, March 17, 2011
- ↑ Re: On internal iterative deeping by Don Dailey, CCC, March 15, 2011
- ↑ CUT/ALL nodes ratio by Daniel Shawul, CCC, June 06, 2013
- ↑ Re: "CUT" vs "ALL" nodes by Robert Hyatt, CCC, March 08, 2011