Difference between revisions of "NegaScout"
GerdIsenberg (talk | contribs) |
GerdIsenberg (talk | contribs) |
||
| Line 121: | Line 121: | ||
* [https://www.stmintz.com/ccc/index.php?id=379100 negascout and PVS?] by [[Peter Aloysius Harjanto|Peter Alloysius]], [[CCC]], July 26, 2004 | * [https://www.stmintz.com/ccc/index.php?id=379100 negascout and PVS?] by [[Peter Aloysius Harjanto|Peter Alloysius]], [[CCC]], July 26, 2004 | ||
* [http://www.talkchess.com/forum/viewtopic.php?t=24883 when to try zero window search] by Andrew Short, [[CCC]], November 14, 2008 | * [http://www.talkchess.com/forum/viewtopic.php?t=24883 when to try zero window search] by Andrew Short, [[CCC]], November 14, 2008 | ||
| − | * [http://www.talkchess.com/forum/viewtopic.php?t=60719 PVS/NegaScout: Actual benefits] by Vincent Tang, [[CCC]], July 06, 2016 | + | * [http://www.talkchess.com/forum/viewtopic.php?t=60719 PVS/NegaScout: Actual benefits] by [[Vincent Tang]], [[CCC]], July 06, 2016 |
=External Links= | =External Links= | ||
Latest revision as of 20:59, 2 March 2020
NegaScout,
an Alpha-Beta enhancement and improvement of Judea Pearl's Scout-algorithm [1], introduced by Alexander Reinefeld in 1983 [2]. The improvements rely on a Negamax framework and some fail-soft issues concerning the two last plies, which did not require any re-searches.
Contents
NegaScout vs. PVS
NegaScout works similar to Tony Marsland's and Murray Campbell's PVS [3]. NegaScout's fail-soft refinements always returns correct minimax scores at the two lowest levels, since it assumes that all horizon nodes would have the same score for the (in that case redundant) re-search, which most programs can not guarantee due to possible extensions [4] and possible bound dependency of quiescence search and evaluation. NegaScout just searches the first move with an open window, and then every move after that with a zero window, whether alpha was already improved or not. Some PVS implementations wait until an alpha-improvement before using zero window at PV-Nodes [5].
Reinefeld's original implementation introduces one additional variable on the stack (only b, since after a = alpha, alpha is not needed any longer), for a slightly simpler control structure than PVS. It has therefor set a new null window at the end of the loop (b = a + 1), but has to consider the move count for the re-search condition though. His implementation trusts the null-window score, even if the re-search doesn't confirm the alpha increase, possibly due to search instability.
While re-searching, NegaScout uses the narrower window of {score, beta}, while other implementations dealing with search instability, re-search with {alpha, beta}. Practically, due to Quiescence Search, and fail-soft implementations of PVS, the two algorithms are essentially equivalent to each other - they expand the same search tree [6][7].
Guido Schimmels
Guido Schimmels in a CCC post on the difference of PVS vs. Negascout [8]:
The difference is how they handle re-searches: PVS passes alpha/beta while NegaScout passes the value returned by the null window search instead of alpha. But then you can get a fail-low on the research due to search anonomalies. If that happens NegaScout returns the value from the first search. That means you will have a crippled PV. Then there is a refinement Reinefeld suggests which is to ommit the re-search at the last two plies (depth > 1) - but that won't work in a real program because of search extensions. NegaScout is slightly an ivory tower variant of PVS (IMHO).
PVS:
value = PVS(-(alpha+1),-alpha)
if(value > alpha && value < beta) {
value = PVS(-beta,-alpha);
}
NegaScout:
value = NegaScout(-(alpha+1),-alpha)
if(value > alpha && value < beta && depth > 1) {
value2 = NegaScout(-beta,-value)
value = max(value,value2);
}
Yngvi Björnsson
Quote by Yngvi Björnsson from CCC, January 05, 2000 [9]:
Search-wise PVS and Negascout are identical (except the deep-cutoffs on the PV you mention), they are just formulated differently. In Negascout the same routine is used for searching both the PV and the rest of the tree, whereas PVS is typically formulated as two routines: PVS (for searching the PV) and NWS (for the null-window searches). Negascout and PVS were developed about the same time in the early '80 (82-83), but independently. I guess, that's part of the reason we know them by different names. Personally, I've always found the PVS/NWS formulation the most intuative, it's easier to understand what's really going on.
Dennis Breuker
Quote by Dennis Breuker from CCC, July 28, 2004 [10]:
Q: What's the different between negascout and PVS ? They look like the same algorithm to me.
They are identical, see note 15 on page 22 of my thesis [11]: We note that the version of principal-variation search as mentioned by Marsland (1986) [12] is identical to the version of negascout as mentioned by Reinefeld (1989) [13]. We use the 1989 reference instead of 1983 [14], which was the first source of this algorithm, since the algorithm described in Reinefeld (1983) contains minor errors.
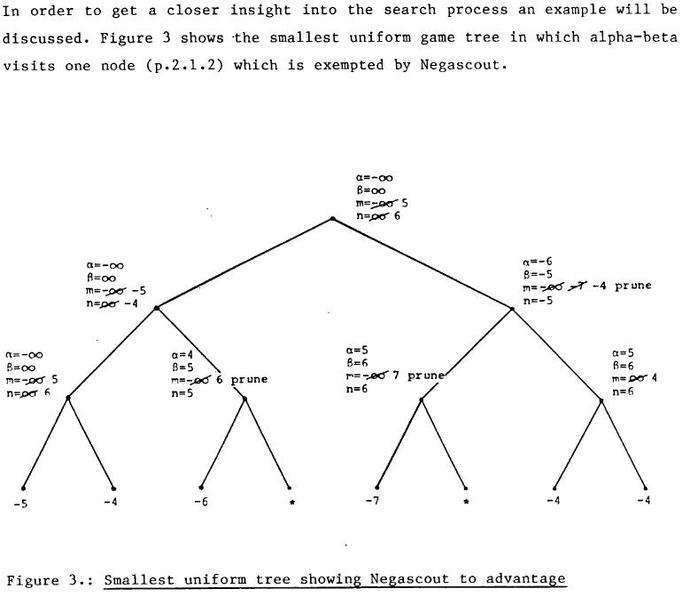
Smallest uniform Tree
Smallest uniform Tree showing Negascout's advantage over Alpha-Beta [15]:
Pseudo C Code
Original
int NegaScout ( position p; int alpha, beta )
{ /* compute minimax value of position p */
int a, b, t, i;
if ( d == maxdepth )
return Evaluate(p); /* leaf node */
determine successors p_1,...,p_w of p;
a = alpha;
b = beta;
for ( i = 1; i <= w; i++ ) {
t = -NegaScout ( p_i, -b, -a );
if ( (t > a) && (t < beta) && (i > 1) && (d < maxdepth-1) )
a = -NegaScout ( p_i, -beta, -t ); /* re-search */
a = max( a, t );
if ( a >= beta )
return a; /* cut-off */
b = a + 1; /* set new null window */
}
return a;
}
Alternative
Following implementation addresses the mentioned issues, wider window for re-searches:
int NegaScout ( position p; int alpha, beta )
{ /* compute minimax value of position p */
int b, t, i;
if ( d == maxdepth )
return quiesce(p, alpha, beta); /* leaf node */
determine successors p_1,...,p_w of p;
b = beta;
for ( i = 1; i <= w; i++ ) {
t = -NegaScout ( p_i, -b, -alpha );
if ( (t > a) && (t < beta) && (i > 1) )
t = -NegaScout ( p_i, -beta, -alpha ); /* re-search */
alpha = max( alpha, t );
if ( alpha >= beta )
return alpha; /* cut-off */
b = alpha + 1; /* set new null window */
}
return alpha;
}
See also
- Alpha-Beta
- Enhanced Forward Pruning
- Iterative Deepening
- Move Ordering
- MTD(f)
- Null Window
- Principal Variation Search
- PVS and Aspiration
- Scout
Publications
- Judea Pearl (1980). Scout: A Simple Game-Searching Algorithm with Proven Optimal Properties. Proceedings of the First Annual National Conference on Artificial Intelligence. Stanford. pdf
- Alexander Reinefeld (1983). An Improvement to the Scout Tree-Search Algorithm. ICCA Journal, Vol. 6, No. 4, pdf
- Agata Muszycka, Rajjan Shinghal (1985). An empirical comparison of pruning strategies in game trees. IEEE Transactions on Systems, Man, and Cybernetics, Vol. 15, No. 3
- Alexander Reinefeld, Tony Marsland (1987). A Quantitative Analysis of Minimal Window Search. IJCAI-87, pdf
- Hung-Jui Chang, Meng-Tsung Tsai, Tsan-sheng Hsu (2011). Game Tree Search with Adaptive Resolution. Advances in Computer Games 13, pdf
Forum Posts
- nega-scout in gnuchess by Bruce Moreland, gnu.chess, June 16, 1994
- Re: Zero-width Window Null Move Search by Guido Schimmels, CCC, June 18, 1998 » Principal Variation Search
- negascout vs pvs by vitor, CCC, June 04, 1999
- PVS and NegaScout by Gian-Carlo Pascutto, CCC, January 05, 2000
- A Question on simple Alpha-Beta versus PVS/Negascout by Andrei Fortuna, CCC, March 21, 2000 » Alpha-Beta, Principal Variation Search
- What is Negascout and why is MWS PVS? by Severi Salminen, CCC, November 24, 2000
- Please explain the difference between PVS and NegaScout by Severi Salminen, CCC, March 02, 2001
- negascout and PVS? by Peter Alloysius, CCC, July 26, 2004
- when to try zero window search by Andrew Short, CCC, November 14, 2008
- PVS/NegaScout: Actual benefits by Vincent Tang, CCC, July 06, 2016
External Links
- NegaScout from Wikipedia
- NegaScout - A Minimax Algorithm faster than AlphaBeta by Alexander Reinefeld
References
- ↑ Judea Pearl (1980). Scout: A Simple Game-Searching Algorithm with Proven Optimal Properties. Proceedings of the First Annual National Conference on Artificial Intelligence. Stanford. pdf
- ↑ Alexander Reinefeld (1983). An Improvement to the Scout Tree-Search Algorithm. ICCA Journal, Vol. 6, No. 4, pdf
- ↑ Tony Marsland, Murray Campbell (1982). Parallel Search of Strongly Ordered Game Trees. ACM Comput. Surv. 14(4): 533-551, pdf
- ↑ Re: negascout vs pvs by Dave Gomboc from CCC, June 04, 1999
- ↑ Principal Variation Search from Bruce Moreland's Programming Topics
- ↑ Yngvi Björnsson (2002). Selective Depth-First Game-Tree Search. Ph.D. thesis, University of Alberta
- ↑ Mark Winands, Jaap van den Herik, Jos Uiterwijk, Erik van der Werf (2003). Enhanced forward pruning. Accepted for publication. pdf
- ↑ Re: Zero-width Window Null Move Search by Guido Schimmels, CCC, June 18, 1998
- ↑ Re: PVS and NegaScout by Yngvi Björnsson from CCC, January 05, 2000
- ↑ Negascout == PVS (with references) by Dennis Breuker
- ↑ Dennis M. Breuker (1998). Ph.D. thesis: Memory versus Search in Games
- ↑ Tony Marsland (1986). A Review of Game-Tree Pruning. ICCA Journal, Vol. 9, No. 1, pdf
- ↑ NegaScout - A Minimax Algorithm faster than AlphaBeta
- ↑ Alexander Reinefeld (1983). An Improvement to the Scout Tree-Search Algorithm. ICCA Journal, Vol. 6, No. 4, pdf
- ↑ Smallest uniform Tree showing Negascout to Advatage, image from Reinefeld, A. (1983). An Improvement to the Scout Tree-Search Algorithm. ICCA Journal, Vol. 6, No. 4, pdf
- ↑ NegaScout - A Minimax Algorithm faster than AlphaBeta