Difference between revisions of "Automated Tuning"
GerdIsenberg (talk | contribs) |
GerdIsenberg (talk | contribs) |
||
| Line 236: | Line 236: | ||
=Forum Posts= | =Forum Posts= | ||
==1997 ...== | ==1997 ...== | ||
| − | * [https://groups.google.com/group/rec.games.chess.computer/browse_frm/thread/77f10f072e907302 Evolutionary Evaluation] by [[ | + | * [https://groups.google.com/group/rec.games.chess.computer/browse_frm/thread/77f10f072e907302 Evolutionary Evaluation] by [[Daniel Homan]], [[Computer Chess Forums|rgcc]], September 09, 1997 » [[Evaluation]] |
* [https://www.stmintz.com/ccc/index.php?id=13794 Deep Blue eval function tuning technique] by [[Stuart Cracraft]], [[CCC]], January 08, 1998 » [[Deep Blue]] <ref>[[Thomas Anantharaman]] ('''1997'''). ''Evaluation Tuning for Computer Chess: Linear Discriminant Methods''. [[ICGA Journal#20_4|ICCA Journal, Vol. 20, No. 4]]</ref> | * [https://www.stmintz.com/ccc/index.php?id=13794 Deep Blue eval function tuning technique] by [[Stuart Cracraft]], [[CCC]], January 08, 1998 » [[Deep Blue]] <ref>[[Thomas Anantharaman]] ('''1997'''). ''Evaluation Tuning for Computer Chess: Linear Discriminant Methods''. [[ICGA Journal#20_4|ICCA Journal, Vol. 20, No. 4]]</ref> | ||
* [https://www.stmintz.com/ccc/index.php?id=13968 Automated Tuning] by [[Stuart Cracraft]], [[CCC]], January 12, 1998 | * [https://www.stmintz.com/ccc/index.php?id=13968 Automated Tuning] by [[Stuart Cracraft]], [[CCC]], January 12, 1998 | ||
Revision as of 15:01, 22 January 2019
Home * Automated Tuning

Automated Tuning,
an automated adjustment of evaluation parameters or weights, and less commonly, search parameters [2], with the aim to improve the playing strength of a chess engine or game playing program. Evaluation tuning can be applied by mathematical optimization or machine learning, both fields with huge overlaps. Learning approaches are subdivided into supervised learning using labeled data, and reinforcement learning to learn from trying, facing the exploration (of uncharted territory) and exploitation (of current knowledge) dilemma. Johannes Fürnkranz gives a comprehensive overview in Machine Learning in Games: A Survey published in 2000 [3], covering evaluation tuning in chapter 4.
Contents
Playing Strength
A difficulty in tuning and automated tuning of engine parameters is measuring playing strength. Using small sets of test-positions, which was quite common in former times to estimate relative strength of chess programs, lacks adequate diversity for a reliable strength predication. In particular, solving test-positions does not necessarily correlate with practical playing strength in matches against other opponents. Therefore, measuring strength requires to play many games against a reference opponent to determine the win rate with a certain confidence. The closer the strength of two opponents, the more games are necessary to determine whether changed parameters or weights in one of them are improvements or not, up to several tens of thousands. Playing many games with ultra short time controls has became de facto standard with todays strong programs, as for instance applied in Stockfish's Fishtest, using the sequential probability ratio test (SPRT) to possibly terminate a match early [4].
Parameter
Quote by Ingo Althöfer [5] [6]:
It is one of the best arts to find the right SMALL set of parameters and to tune them.
Some 12 years ago I had a technical article on this ("On telescoping linear evaluation functions") in the ICCA Journal, Vol. 16, No. 2, pp. 91-94, describing a theorem (of existence) which says that in case of linear evaluation functions with lots of terms there is always a small subset of the terms such that this set with the right parameters is almost as good as the full evaluation function.
Mathematical Optimization
Mathematical optimization methods in tuning consider the engine as a black box.
Methods
Instances
Advantages
- Works with all engine parameters, including search
- Takes search-eval interaction into account
Disadvantages
- Time complexity issues with increasing number of weights to tune
Reinforment Learning
Reinforcement learning, in particular temporal difference learning, has a long history in tuning evaluation weights in game programming, first seeen in the late 50s by Arthur Samuel in his Checkers player [7]. In self play against a stable copy of itself, after each move, the weights of the evaluation function were adjusted in a way that the score of the root position after a quiescence search became closer to the score of the full search. This TD method was generalized and formalized by Richard Sutton in 1988 [8], who introduced the decay parameter λ, where proportions of the score came from the outcome of Monte Carlo simulated games, tapering between bootstrapping (λ = 0) and Monte Carlo (λ = 1). TD-λ was famously applied by Gerald Tesauro in his Backgammon program TD-Gammon [9] [10], its minimax adaption TD-Leaf was successful used in eval tuning of chess programs [11], with KnightCap [12] and CilkChess [13] as prominent samples.
Instances
Engines
Supervised Learning
Move Adaption
One supervised learning method considers desired moves from a set of positions, likely from grandmaster games, and tries to adjust their evaluation weights so that for instance a one-ply search agrees with the desired move. Already pioneering in reinforcement learning some years before, move adaption was described by Arthur Samuel in 1967 as used in the second version of his checkers player [15], where a structure of stacked linear evaluation functions was trained by computing a correlation measure based on the number of times the feature rated an alternative move higher than the desired move played by an expert [16]. In chess, move adaption was first described by Thomas Nitsche in 1982 [17], and with some extensions by Tony Marsland in 1985 [18]. Eval Tuning in Deep Thought as mentioned by Feng-hsiung Hsu et al. in 1990 [19], and later published by Andreas Nowatzyk, is also based on an extended form of move adaption [20]. Jonathan Schaeffer's and Paul Lu's efforts to make Deep Thought's approach work for Chinook in 1990 failed [21] - nothing seemed to produce results that were as good than their hand-tuned effort [22].
Value Adaption
A second supervised learning approach used to tune evaluation weights is based on regression of the desired value, i.e. using the final outcome from huge sets of positions from quality games, or other information supplied by a supervisor, i.e. in form of annotations from position evaluation symbols. Often, value adaption is reinforced by determining an expected outcome by self play [23].
Advantages
- Can modify any number of weights simultaneously - constant time complexity
Disadvantages
- Requires a source for the labeled data
- Can only be used for evaluation weights or anything else that can be labeled
- Works not optimal when combined with search
Regression
Regression analysis is a statistical process with a substantial overlap with machine learning to predict the value of an Y variable (output), given known value pairs of the X and Y variables. While linear regression deals with continuous outputs, logistic regression covers binary or discrete output, such as win/loss, or win/draw/loss. Parameter estimation in regression analysis can be formulated as the minimization of a cost or loss function over a training set [24], such as mean squared error or cross-entropy error function for binary classification [25]. The minimization is implemented by iterative optimization algorithms or metaheuristics such as Iterated local search, Gauss–Newton algorithm, or conjugate gradient method.
Linear Regression
| The supervised problem of regression applied to move adaption was used by Thomas Nitsche in 1982, minimizing the mean squared error of a cost function considering the program’s and a grandmaster’s choice of moves, as mentioned, extended by Tony Marsland in 1985, and later by the Deep Thought team. Regression used to adapt desired values was described by Donald H. Mitchell in his 1984 masters thesis on evaluation features in Othello, cited by Michael Buro [26] [27]. Jens Christensen applied linear regression to chess in 1986 to learn point values in the domain of temporal difference learning [28]. |
Logistic Regression
| Since the relationship between win percentage and pawn advantage is assumed to follow a logistic model, one may treat static evaluation as single-layer perceptron or single neuron ANN with the common logistic activation function, performing the perceptron algorithm to train it [30]. Logistic regression in evaluation tuning was first elaborated by Michael Buro in 1995 [31], and proved successful in the game of Othello in comparison with Fisher's linear discriminant and quadratic discriminant function for normally distributed features, and served as eponym of his Othello program Logistello [32]. In computer chess, logistic regression was proposed by Miguel A. Ballicora in a 2009 CCC post, as applied to Gaviota [33], was independently described by Amir Ban in 2012 for Junior's evaluation learning [34], and explicitly mentioned by Álvaro Begué in a January 2014 CCC discussion [35], when Peter Österlund explained Texel's Tuning Method [36], which subsequently popularized logistic regression tuning in computer chess. Vladimir Medvedev's Point Value by Regression Analysis [37] [38] experiments showed why the logistic function is appropriate, and further used cross-entropy and regularization. |
Instances
- Arasan's Tuning
- Eval Tuning in Deep Thought
- Minimax Tree Optimization (MMTO or the Bonanza-Method in Shogi)
- Point Value by Regression Analysis
- RuyTune
- Texel's Tuning Method
- Winter
See also
- Dynamic Programming
- Evaluation
- GLEM by Michael Buro
- Iteration
- Knowledge
- Learning
- Match Statistics
- Neural Networks
- Trial and Error
Publications
1959
- Arthur Samuel (1959). Some Studies in Machine Learning Using the Game of Checkers. IBM Journal July 1959
1960 ...
- Arnold K. Griffith (1966). A new Machine-Learning Technique applied to the Game of Checkers. MIT, Project MAC, MAC-M-293
- Arthur Samuel (1967). Some Studies in Machine Learning. Using the Game of Checkers. II-Recent Progress. pdf
1970 ...
- Arnold K. Griffith (1974). A Comparison and Evaluation of Three Machine Learning Procedures as Applied to the Game of Checkers. Artificial Intelligence, Vol. 5, No. 2
1980 ...
- Thomas Nitsche (1982). A Learning Chess Program. Advances in Computer Chess 3
- Donald H. Mitchell (1984). Using Features to Evaluate Positions in Experts' and Novices' Othello Games. Masters thesis, Department of Psychology, Northwestern University, Evanston, IL
1985 ...
- Tony Marsland (1985). Evaluation-Function Factors. ICCA Journal, Vol. 8, No. 2, pdf
- Jens Christensen, Richard Korf (1986). A Unified Theory of Heuristic Evaluation functions and Its Applications to Learning. Proceedings of the AAAI-86, pp. 148-152, pdf
- Jens Christensen (1986). Learning Static Evaluation Functions by Linear Regression. in Tom Mitchell, Jaime Carbonell, Ryszard Michalski (1986). Machine Learning: A Guide to Current Research. The Kluwer International Series in Engineering and Computer Science, Vol. 12
- Dap Hartmann (1987). How to Extract Relevant Knowledge from Grandmaster Games. Part 1: Grandmasters have Insights - the Problem is what to Incorporate into Practical Problems. ICCA Journal, Vol. 10, No. 1
- Dap Hartmann (1987). How to Extract Relevant Knowledge from Grandmaster Games. Part 2: the Notion of Mobility, and the Work of De Groot and Slater. ICCA Journal, Vol. 10, No. 2
- Bruce Abramson, Richard Korf (1987). A Model of Two-Player Evaluation Functions. AAAI-87. pdf
- Bruce Abramson (1988). Learning Expected-Outcome Evaluators in Chess. Proceedings of the 1988 AAAI Spring Symposium Series: Computer Game Playing, 26-28.
- Kai-Fu Lee, Sanjoy Mahajan (1988). A Pattern Classification Approach to Evaluation Function Learning. Artificial Intelligence, Vol. 36, No. 1
- Richard Sutton (1988). Learning to Predict by the Methods of Temporal Differences. Machine Learning, Vol. 3, No. 1, pdf
- Bruce Abramson (1989). On Learning and Testing Evaluation Functions. Proceedings of the Sixth Israeli Conference on Artificial Intelligence, 1989, 7-16.
- Maarten van der Meulen (1989). Weight Assessment in Evaluation Functions. Advances in Computer Chess 5
1990 ...
- Bruce Abramson (1990). Expected-Outcome: A General Model of Static Evaluation. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 12, No. 2
- Bruce Abramson (1990). An Analysis of Expected-Outcome. Journal of Experimental and Theoretical Artificial Intelligence 2: 55-73.
- Bruce Abramson (1990). On Learning and Testing Evaluation Functions. Journal of Experimental and Theoretical Artificial Intelligence, Vol. 2
- Thomas Anantharaman (1990). A Statistical Study of Selective Min-Max Search in Computer Chess. Ph.D. thesis, Carnegie Mellon University
- Thomas Anantharaman (1991). A Statistical Study of Selective Min-Max Search in Computer Chess. ICCA Journal, Vol. 14, No. 1
- Feng-hsiung Hsu, Thomas Anantharaman, Murray Campbell, Andreas Nowatzyk (1990). A Grandmaster Chess Machine. Scientific American, Vol. 263, No. 4, pp. 44-50. ISSN 0036-8733.
- Bruce Abramson (1991). The Expected-Outcome Model of Two-Player Games. Part of the series, Research Notes in Artificial Intelligence (San Mateo: Morgan Kaufmann, 1991).
- Alex van Tiggelen (1991). Neural Networks as a Guide to Optimization - The Chess Middle Game Explored. ICCA Journal, Vol. 14, No. 3
- William Tunstall-Pedoe (1991). Genetic Algorithms Optimizing Evaluation Functions. ICCA Journal, Vol. 14, No. 3
- Paul E. Utgoff, Jeffery A. Clouse (1991). Two Kinds of Training Information for Evaluation Function Learning. University of Massachusetts, Amherst, Proceedings of the AAAI 1991
- Gerald Tesauro (1992). Temporal Difference Learning of Backgammon Strategy. ML 1992
- Ingo Althöfer (1993). On Telescoping Linear Evaluation Functions. ICCA Journal, Vol. 16, No. 2, pp. 91-94
- Peter Mysliwietz (1994). Konstruktion und Optimierung von Bewertungsfunktionen beim Schach. Ph.D. thesis (German)
1995 ...
- Michael Buro (1995). Statistical Feature Combination for the Evaluation of Game Positions. JAIR, Vol. 3
- Chris McConnell (1995). Tuning Evaluation Functions for Search. pdf
- Chris McConnell (1995). Tuning Evaluation Functions for Search (Talk), ps
- Johannes Fürnkranz (1996). Machine Learning in Computer Chess: The Next Generation. ICCA Journal, Vol. 19, No. 3, zipped ps
- Don Beal, Martin C. Smith (1997). Learning Piece Values Using Temporal Differences. ICCA Journal, Vol. 20, No. 3
- Thomas Anantharaman (1997). Evaluation Tuning for Computer Chess: Linear Discriminant Methods. ICCA Journal, Vol. 20, No. 4
- Jonathan Baxter, Andrew Tridgell, Lex Weaver (1998). Experiments in Parameter Learning Using Temporal Differences. ICCA Journal, Vol. 21, No. 2, pdf
- Michael Buro (1998). From Simple Features to Sophisticated Evaluation Functions. CG 1998, pdf
- James C. Spall (1998). Implementation of the Simultaneous Perturbation Algorithm for Stochastic Optimization. IEEE Transactions on Aerospace and Electronic Systems, pdf [40]
- Don Beal, Martin C. Smith (1999). Learning Piece-Square Values using Temporal Differences. ICCA Journal, Vol. 22, No. 4
2000 ...
- Johannes Fürnkranz (2000). Machine Learning in Games: A Survey. Austrian Research Institute for Artificial Intelligence, OEFAI-TR-2000-3, pdf
- Robert Levinson, Ryan Weber (2000). Chess Neighborhoods, Function Combination, and Reinforcement Learning. CG 2000, pdf
- Johannes Fürnkranz, Miroslav Kubat (eds.) (2001). Machines that Learn to Play Games. Advances in Computation: Theory and Practice, Vol. 8,. NOVA Science Publishers
- Graham Kendall, Glenn Whitwell (2001). An Evolutionary Approach for the Tuning of a Chess Evaluation Function using Population Dynamics. Proceedings of the 2001 Congress on Evolutionary Computation, Vol. 2, pdf
- Yngvi Björnsson, Tony Marsland (2001). Learning Search Control in Adversary Games. Advances in Computer Games 9, pp. 157-174. pdf
- Michael Buro (2002). Improving Mini-max Search by Supervised Learning. Artificial Intelligence, Vol. 134, No. 1, pdf
- Dave Gomboc, Tony Marsland, Michael Buro (2003). Evaluation Function Tuning via Ordinal Correlation. Advances in Computer Games 10, pdf
- Dave Gomboc (2004). Tuning Evaluation Functions by Maximizing Concordance. M.Sc. Thesis, University of Alberta
- Adam Marczyk (2004). Genetic Algorithms and Evolutionary Computation from the TalkOrigins Archive
- Petr Aksenov (2004). Genetic algorithms for optimising chess position scoring, Master's thesis, pdf
- Mathieu Autonès, Aryel Beck, Phillippe Camacho, Nicolas Lassabe, Hervé Luga, François Scharffe (2004). Evaluation of Chess Position by Modular Neural network Generated by Genetic Algorithm. EuroGP 2004
- Henk Mannen, Marco Wiering (2004). Learning to play chess using TD(λ)-learning with database games. Cognitive Artificial Intelligence, Utrecht University, Benelearn’04
2005 ...
- Dave Gomboc, Michael Buro, Tony Marsland (2005). Tuning Evaluation Functions by Maximizing Concordance. Theoretical Computer Science, Vol. 349, No. 2, pdf
- Jeff Rollason (2005). Evaluation by Hill-climbing: Getting the right move by solving micro-problems. AI Factory, Autumn 2005
- Levente Kocsis, Csaba Szepesvári, Mark Winands (2005). RSPSA: Enhanced Parameter Optimization in Games. Advances in Computer Games 11, pdf
2006
- Levente Kocsis, Csaba Szepesvári (2006). Universal Parameter Optimisation in Games Based on SPSA. Machine Learning, Special Issue on Machine Learning and Games, Vol. 63, No. 3
- Hallam Nasreddine, Hendra Suhanto Po, Graham Kendall (2006). Using an Evolutionary Algorithm for the Tuning of a Chess Evaluation Function Based on a Dynamic Boundary Strategy. Proceedings of the 2006 IEEE Conference on Cybernetics and Intelligent Systems, pdf
- Makoto Miwa, Daisaku Yokoyama, Takashi Chikayama (2006). Automatic Construction of Static Evaluation Functions for Computer Game Players. ALT ’06
- Borko Bošković, Sašo Greiner, Janez Brest, Viljem Žumer (2006). A Differential Evolution for the Tuning of a Chess Evaluation Function. IEEE Congress on Evolutionary Computation
- Kunihito Hoki (2006). Optimal control of minimax search result to learn positional evaluation. 11th Game Programming Workshop (Japanese)
2007
- Shogo Takeuchi, Tomoyuki Kaneko, Kazunori Yamaguchi, Satoru Kawai (2007). Visualization and Adjustment of Evaluation Functions Based on Evaluation Values and Win Probability. AAAI 2007, pdf
- Makoto Miwa, Daisaku Yokoyama, Takashi Chikayama (2007). Automatic Generation of Evaluation Features for Computer Game Players. pdf
- Johannes Fürnkranz (2007). Recent advances in machine learning and game playing. ÖGAI Journal, Vol. 26, No. 2, Computer Game Playing, pdf
2008
- Omid David, Moshe Koppel, Nathan S. Netanyahu (2008). Genetic Algorithms for Mentor-Assisted Evaluation Function Optimization. GECCO '08, arXiv:1711.06839
- Borko Bošković, Sašo Greiner, Janez Brest, Aleš Zamuda, Viljem Žumer (2008). An Adaptive Differential Evolution Algorithm with Opposition-Based Mechanisms, Applied to the Tuning of a Chess Program. Advances in Differential Evolution, Springer
2009
- Joel Veness, David Silver, William Uther, Alan Blair (2009). Bootstrapping from Game Tree Search. Neural Information Processing Systems (NIPS), 2009, pdf
- Omid David, Jaap van den Herik, Moshe Koppel, Nathan S. Netanyahu (2009). Simulating Human Grandmasters: Evolution and Coevolution of Evaluation Functions. GECCO '09, arXiv:1711.0684
- Omid David (2009). Genetic Algorithms Based Learning for Evolving Intelligent Organisms. Ph.D. Thesis.
- Broch Davison (2009). Playing Chess with Matlab. M.Sc. thesis supervised by Nello Cristianini, pdf [41]
- Mark Levene, Trevor Fenner (2009). A Methodology for Learning Players' Styles from Game Records. arXiv:0904.2595v1
- Wei-Lun Kao (2009). The Automatically Tuning System of Evaluation Function for Computer Chinese Chess. Master thesis, National Chiao Tung University, pdf (Chinese)
2010 ...
- Amine Bourki, Matthieu Coulm, Philippe Rolet, Olivier Teytaud, Paul Vayssière (2010). Parameter Tuning by Simple Regret Algorithms and Multiple Simultaneous Hypothesis Testing. pd
- Omid David, Moshe Koppel, Nathan S. Netanyahu (2010). Genetic Algorithms for Automatic Search Tuning. ICGA Journal, Vol. 33, No. 2
- Borko Bošković (2010). Differential Evolution for the Tuning of a Chess Evaluation Function. Ph.D. thesis, University of Maribor
2011
- Omid David, Moshe Koppel, Nathan S. Netanyahu (2011). Expert-Driven Genetic Algorithms for Simulating Evaluation Functions. Genetic Programming and Evolvable Machines, Vol. 12, No. 1, arXiv:1711.06841
- Borko Bošković, Janez Brest (2011). Tuning Chess Evaluation Function Parameters using Differential Evolution. Informatica, Vol. 35, No. 2
- Borko Bošković, Janez Brest, Aleš Zamuda, Sašo Greiner, Viljem Žumer (2011). History mechanism supported differential evolution for chess evaluation function tuning. Soft Computing, Vol. 15, No. 4
- Eduardo Vázquez-Fernández, Carlos Artemio Coello Coello, Feliú Davino Sagols Troncoso (2011). An Evolutionary Algorithm for Tuning a Chess Evaluation Function. CEC 2011, pdf
- Eduardo Vázquez-Fernández, Carlos Artemio Coello Coello, Feliú Davino Sagols Troncoso (2011). An Adaptive Evolutionary Algorithm Based on Typical Chess Problems for Tuning a Chess Evaluation Function. GECCO 2011, pdf
- Rémi Coulom (2011). CLOP: Confident Local Optimization for Noisy Black-Box Parameter Tuning. Advances in Computer Games 13 [42] [43]
- Kunihito Hoki, Tomoyuki Kaneko (2011). The Global Landscape of Objective Functions for the Optimization of Shogi Piece Values with a Game-Tree Search. Advances in Computer Games 13 » Shogi
2012
- Amir Ban (2012). Automatic Learning of Evaluation, with Applications to Computer Chess. Discussion Paper 613, The Hebrew University of Jerusalem - Center for the Study of Rationality, Givat Ram
- Kanjanapa Thitipong, Komiya Kanako, Yoshiyuki Kotani (2012). Design and Implementation of Bonanza Method for the Evaluation in the Game of Arimaa. IPSJ SIG Technical Report, Vol. 2012-GI-27, No. 4, pdf » Arimaa
2013
- Wen-Jie Tseng, Jr-Chang Chen, I-Chen Wu, Ching-Hua Kuo, Bo-Han Lin (2013). A Supervised Learning Method for Chinese Chess Programs. JSAI2013, pdf
- Akira Ura, Makoto Miwa, Yoshimasa Tsuruoka, Takashi Chikayama (2013). Comparison Training of Shogi Evaluation Functions with Self-Generated Training Positions and Moves. CG 2013, slides as pdf
- Yoshikuni Sato, Makoto Miwa, Shogo Takeuchi, Daisuke Takahashi (2013). Optimizing Objective Function Parameters for Strength in Computer Game-Playing. AAAI 2013
- Shalabh Bhatnagar, H. L. Prasad, L.A. Prashanth (2013). Stochastic Recursive Algorithms for Optimization: Simultaneous Perturbation Methods. Lecture Notes in Control and Information Sciences, Vol. 434, Springer » SPSA
- Tomáš Hřebejk (2013). Arimaa challenge - Static Evaluation Function. Master Thesis, Charles University in Prague, pdf » Arimaa [44]
- Yoshikuni Sato, Makoto Miwa, Shogo Takeuchi, Daisuke Takahashi (2013). Optimizing Objective Function Parameters for Strength in Computer Game-Playing. AAAI 2013
2014
- Kunihito Hoki, Tomoyuki Kaneko (2014). Large-Scale Optimization for Evaluation Functions with Minimax Search. JAIR Vol. 49, pdf » Shogi [45]
- Aryan Mokhtari, Alejandro Ribeiro (2014). RES: Regularized Stochastic BFGS Algorithm. arXiv:1401.7625 [46]
- Jemin Hwangbo, Christian Gehring, Hannes Sommer, Roland Siegwart, Jonas Buchli (2014). ROCK∗ — Efficient black-box optimization for policy learning. Humanoids, 2014 » Rockstar
- James Martens (2014, 2017). New insights and perspectives on the natural gradient method. arXiv:1412.1193
2015 ...
- Diederik P. Kingma, Jimmy Lei Ba (2015). Adam: A Method for Stochastic Optimization. arXiv:1412.6980v8, ICLR 2015 [47]
- Aryan Mokhtari, Alejandro Ribeiro (2015). Global Convergence of Online Limited Memory BFGS. Journal of Machine Learning Research, Vol. 16, pdf [48] [49]
2016
2017
- Sebastian Ruder (2017). An overview of gradient descent optimization algorithms. arXiv:1609.04747v2 [50]
- Hung-Jui Chang, Gang-Yu Fan, Jr-Chang Chen, Chih-Wen Hsueh, Tsan-sheng Hsu (2017). Validating and Fine-Tuning of Game Evaluation Functions Using Endgame Databases. CGW@IJCAI 2017
2018
- Takafumi Nakamichi, Takeshi Ito (2018). Adjusting the evaluation function for weakening the competency level of a computer shogi program. ICGA Journal, Vol. 40, No. 1
- Hung-Jui Chang, Jr-Chang Chen, Gang-Yu Fan, Chih-Wen Hsueh, Tsan-sheng Hsu (2018). Using Chinese dark chess endgame databases to validate and fine-tune game evaluation functions. ICGA Journal, Vol. 40, No. 2 » Chinese Dark Chess, Endgame Tablebases
Forum Posts
1997 ...
- Evolutionary Evaluation by Daniel Homan, rgcc, September 09, 1997 » Evaluation
- Deep Blue eval function tuning technique by Stuart Cracraft, CCC, January 08, 1998 » Deep Blue [51]
- Automated Tuning by Stuart Cracraft, CCC, January 12, 1998
- Pattern Matching -- Avoiding Hand-Tuning by Stuart Cracraft, CCC, January 21, 1998
- Speaking of "Evaluate" by Danniel Corbit, CCC, September 29, 1998
- Parameter Tuning by Jonathan Baxter, CCC, October 01, 1998 » TD-learning, KnightCap
2000 ...
- Deep Thought's tuning code and eval function! by Severi Salminen, CCC, September 05, 2000 » Eval Tuning in Deep Thought
- learning to tune parameters by comp-comp games by Uri Blass, CCC, December 28, 2000
- Automatic Eval Tuning by Artem Pyatakov, CCC, June 29, 2001
- deep blue's automatic tuning of evaluation function by Emerson Tan, CCC, March 22, 2003
- evaluationfunction tuning by Jan Willem de Kort, CCC, September 07, 2003
- evaluation tuning tricks by Peter Alloysius, CCC, March 17, 2004
2005 ...
- "learning" or "tuning" programs by Sean Mintz, CCC, February 15, 2006
- Adjusting weights the Deep Blue way by Tony van Roon-Werten, Winboard Forum, August 29, 2008 » Deep Blue
- Tuning the eval by Daniel Anulliero, Winboard Forum, January 02, 2009
- Insanity... or Tal style? by Miguel A. Ballicora, CCC, April 01, 2009
- Re: Insanity... or Tal style? by Miguel A. Ballicora, CCC, April 02, 2009 [52]
2010 ...
- Revisiting GA's for tuning evaluation weights by Ilari Pihlajisto, CCC, January 03, 2010
- Idea for Automatic Calibration of Evaluation Function... by Steve Maughan, CCC, January 22, 2010
- Re: TEST position TCEC5- Houdini 1.03a-DRybka4 1-0 by Milos Stanisavljevic, CCC, November 30, 2010
- Parameter tuning by Onno Garms, CCC, March 13, 2011 » Onno
- Ahhh... the holy grail of computer chess by Marcel van Kervinck, CCC, August 23, 2011
- CLOP for Noisy Black-Box Parameter Optimization by Rémi Coulom, CCC, September 01, 2011 [53]
- Tuning again by Ed Schroder, CCC, November 01, 2011
- Ban: Automatic Learning of Evaluation [...] by BB+, OpenChess Forum, May 10, 2012 [54]
2014
- How Do You Automatically Tune Your Evaluation Tables by Tom Likens, CCC, January 07, 2014
- Re: How Do You Automatically Tune Your Evaluation Tables by Álvaro Begué, CCC, January 08, 2014
- The texel evaluation function optimization algorithm by Peter Österlund, CCC, January 31, 2014 » Texel's Tuning Method
- Re: The texel evaluation function optimization algorithm by Álvaro Begué, CCC, January 31, 2014 » Cross-entropy
- Tuning eval by Daniel Anulliero, CCC, September 01, 2014
- Tune cut margins with Texel/gaviota tuning method by Fabio Gobbato, CCC, September 11, 2014
- Eval tuning - any open source engines with GA or PBIL? by Hrvoje Horvatic, CCC, December 04, 2014 » PBIL
2015 ...
- MMTO for evaluation learning by Jon Dart, CCC, January 25, 2015 [55]
- Experiments with eval tuning by Jon Dart, CCC, March 10, 2015 » Arasan, Texel's Tuning Method
- txt: automated chess engine tuning by Alexandru Mosoi, CCC, March 18, 2015 » Zurichess, Texel's Tuning Method [56]
- Re: txt: automated chess engine tuning by Sergei S. Markoff, CCC, February 15, 2016 » SmarThink
- Piece weights with regression analysis (in Russian) by Vladimir Medvedev, CCC, April 30, 2015 » Point Value by Regression Analysis
- Re: Piece weights with regression analysis (in Russian) by Fabien Letouzey, CCC, May 04, 2015
- New Idea For Automated Tuning by Jordan Bray, CCC, May 16, 2015
- Evaluation Tuning by Michael Hoffmann, CCC, August 09, 2015
- Genetical tuning by Stefano Gemma, CCC, August 11, 2015 » Genetic Programming
- Re: Genetical tuning by Ferdinand Mosca, CCC, August 20, 2015
- Some musings about search by Ed Schroder, CCC, August 14, 2015 » Search
- td-leaf by Alexandru Mosoi, CCC, October 06, 2015
- tensorflow by Alexandru Mosoi, CCC, November 10, 2015 [57]
2016
- pawn hash and eval tuning by J. Wesley Cleveland, CCC, February 21, 2016 » Pawn Hash Table
- Tuning by ppyvabw, OpenChess Forum, June 11, 2016 » Texel's Tuning Method
- GreKo 2015 ML: tuning evaluation (article in Russian) by Vladimir Medvedev, CCC, July 22, 2016 » GreKo, Texel's Tuning Method
- A database for learning evaluation functions by Álvaro Begué, CCC, October 28, 2016 » Evaluation, Learning, Texel's Tuning Method
- CLOP: when to stop? by Erin Dame, CCC, November 07, 2016 » CLOP
- Re: CLOP: when to stop? by Álvaro Begué, CCC, November 08, 2016 [58]
- C++ code for tuning evaluation function parameters by Álvaro Begué, CCC, November 10, 2016 » RuyTune [59]
2017
- improved evaluation function by Alexandru Mosoi, CCC, March 11, 2017 » Texel's Tuning Method, Zurichess
- automated tuning by Stuart Cracraft, CCC, March 13, 2017
- Parameter tuning with multi objective optimization by Marco Pampaloni, CCC, May 07, 2017 » Napoleon
- Evaluation Tuning: When To Stop? by Cheney Nattress, CCC, May 29, 2017
- Texel tuning method question by Sander Maassen vd Brink, CCC, June 05, 2017 » Texel's Tuning Method
- Re: Texel tuning method question by Peter Österlund, CCC, June 07, 2017
- Re: Texel tuning method question by Ferdinand Mosca, CCC, July 20, 2017 » Python
- Re: Texel tuning method question by Jon Dart, CCC, July 23, 2017
- Approximating Stockfish's Evaluation by PSQTs by Thomas Dybdahl Ahle, CCC, August 23, 2017 » Regression, Piece-Square Tables, Stockfish
- Ab-initio evaluation tuning by Evert Glebbeek, CCC, August 30, 2017
- ROCK* black-box optimizer for chess by Jon Dart, CCC, August 31, 2017 » ROCK*, Rockstar
- tuning via maximizing likelihood by Daniel Shawul, CCC, October 04, 2017 [60]
- tool to create derivates of a given function by Alexandru Mosoi, CCC, November 07, 2017
- Re: tool to create derivates of a given function by Daniel Shawul, CCC, November 07, 2017 [61]
- tuning for the uninformed by Folkert van Heusden, CCC, November 23, 2017
2018
- tuning info by Marco Belli, CCC, January 03, 2018
- 3 million games for training neural networks by Álvaro Begué, CCC, February 24, 2018 » Neural Networks
- Introducing PET by Ed Schröder, CCC, June 27, 2018 » Strategic Test Suite
- Texel tuning speed by Vivien Clauzon, CCC, August 29, 2018 » Texel's Tuning Method
- methods for tuning coefficients by Stuart Cracraft, CCC, October 28, 2018
- Particle Swarm Optimization Code by Erik Madsen, CCC, November 24, 2018 » MadChess
External Links
- Practical Engine Tuning by Ed Schröder, June 2018 » Strategic Test Suite [62]
Optimization
- Mathematical optimization from Wikipedia
- Optimization problem from Wikipedia
- Global optimization from Wikipedia
- Iterated local search from Wikipedia
- Local search (optimization) from Wikipedia
- Broyden–Fletcher–Goldfarb–Shanno algorithm from Wikipedia
- CLOP for Noisy Black-Box Parameter Optimization by Rémi Coulom » CLOP [63] [64]
- Conjugate gradient method from Wikipedia
- Convex optimization from Wikipedia
- Entropy maximization from Wikipedia
- Linear programming from Wikipedia
- Simplex algorithm from Wikipedia
- Differential evolution from Wikipedia
- Evolutionary computation from Wikipedia
- Gauss–Newton algorithm from Wikipedia
- Genetic algorithm from Wikipedia
- Gradient descent from Wikipedia
- Hill climbing from Wikipedia
- Limited-memory BFGS from Wikipedia [65]
- Loss function from Wikipedia
- Nelder–Mead method from Wikipedia » Amoeba, Murka
- Newton's method in optimization from Wikipedia
- NOMAD - A blackbox optimization software [66]
- NEWUOA from Wikipedia [67]
- Particle swarm optimization from Wikipedia
- Population-based incremental learning (PBIL) - Wikipedia [68]
- Population Based Incremental Learning (PBIL) by Thomas Petzke, March 16, 2013 » iCE
- Simulated annealing from Wikipedia
- Stochastic optimization from Wikipedia
- Simultaneous perturbation stochastic approximation (SPSA) - Wikipedia
- SPSA Algorithm
- Stochastic approximation from Wikipedia
- Stochastic gradient descent from Wikipedia
Machine Learning
- Machine learning from Wikipedia
- List of machine learning concepts from Wikipedia
- Backpropagation from Wikipedia » Neural Networks
- Reinforcement learning from Wikipedia
Statistics/Regression Analysis
- Regression analysis from Wikipedia
- Outline of regression analysis from Wikipedia
- Bayesian linear regression from Wikipedia
- Bayesian multivariate linear regression from Wikipedia
- Correlation does not imply causation from Wikipedia
- Cross entropy from Wikipedia
- Elastic net regularization from Wikipedia
- LASSO from Wikipedia
- Likelihood function from Wikipedia
- Linear regression from Wikipedia
- Linear discriminant analysis from Wikipedia
- Logistic regression from Wikipedia
- Kernel Fisher discriminant analysis from Wikipedia
- Maximum likelihood estimation from Wikipedia
- Mean squared error from Wikipedia
- Nonlinear regression from Wikipedia
- Ordinary least squares from Wikipedia
- Polynomial regression from Wikipedia
- Simple linear regression from Wikipedia
- Tikhonov regularization (Ridge regression) from Wikipedia
Code
- alonamaloh / ruy_tune — Bitbucket » RuyTune by Álvaro Begué
- Rockstar: Implementation of ROCK* algorithm (Gaussian kernel regression + natural gradient descent) for optimisation | GitHub by Lyudmil Antonov and Joona Kiiski » ROCK* [69]
- SPSA Tuner for Stockfish Chess Engine | GitHub by Joona Kiiski » Stockfish, Stockfish's Tuning Method
Misc
- The Next Step Quintet feat. Tivon Pennicott - Regression, KerameioBar Athens, Greece, September 2014, YouTube Video
References
- ↑ A vintage motor engine tester located at the James Hall museum of Transport, Johannesburg, South Africa - Engine tuning from Wikipedia
- ↑ Yngvi Björnsson, Tony Marsland (2001). Learning Search Control in Adversary Games. Advances in Computer Games 9, pp. 157-174. pdf
- ↑ Johannes Fürnkranz (2000). Machine Learning in Games: A Survey. Austrian Research Institute for Artificial Intelligence, OEFAI-TR-2000-3, pdf - Chapter 4, Evaluation Function Tuning
- ↑ Fishtest Distributed Testing Framework by Marco Costalba, CCC, May 01, 2013
- ↑ Re: Zappa Report by Ingo Althöfer, CCC, December 30, 2005 » Zappa
- ↑ Ingo Althöfer (1993). On Telescoping Linear Evaluation Functions. ICCA Journal, Vol. 16, No. 2, pp. 91-94
- ↑ Arthur Samuel (1959). Some Studies in Machine Learning Using the Game of Checkers. IBM Journal July 1959
- ↑ Richard Sutton (1988). Learning to Predict by the Methods of Temporal Differences. Machine Learning, Vol. 3, No. 1, pdf
- ↑ Gerald Tesauro (1992). Temporal Difference Learning of Backgammon Strategy. ML 1992
- ↑ Gerald Tesauro (1994). TD-Gammon, a Self-Teaching Backgammon Program, Achieves Master-Level Play. Neural Computation Vol. 6, No. 2
- ↑ Don Beal, Martin C. Smith (1999). Learning Piece-Square Values using Temporal Differences. ICCA Journal, Vol. 22, No. 4
- ↑ Jonathan Baxter, Andrew Tridgell, Lex Weaver (1998). Experiments in Parameter Learning Using Temporal Differences. ICCA Journal, Vol. 21, No. 2, pdf
- ↑ The Cilkchess Parallel Chess Program
- ↑ EXchess also uses CLOP
- ↑ Arthur Samuel (1967). Some Studies in Machine Learning. Using the Game of Checkers. II-Recent Progress. pdf
- ↑ Johannes Fürnkranz (2000). Machine Learning in Games: A Survey. Austrian Research Institute for Artificial Intelligence, OEFAI-TR-2000-3, pdf
- ↑ Thomas Nitsche (1982). A Learning Chess Program. Advances in Computer Chess 3
- ↑ Tony Marsland (1985). Evaluation-Function Factors. ICCA Journal, Vol. 8, No. 2, pdf
- ↑ Feng-hsiung Hsu, Thomas Anantharaman, Murray Campbell, Andreas Nowatzyk (1990). A Grandmaster Chess Machine. Scientific American, Vol. 263, No. 4, pp. 44-50. ISSN 0036-8733.
- ↑ see 2.1 Learning from Desired Moves in Chess in Kunihito Hoki, Tomoyuki Kaneko (2014). Large-Scale Optimization for Evaluation Functions with Minimax Search. JAIR Vol. 49
- ↑ Jonathan Schaeffer, Joe Culberson, Norman Treloar, Brent Knight, Paul Lu, Duane Szafron (1992). A World Championship Caliber Checkers Program. Artificial Intelligence, Vol. 53, Nos. 2-3,ps
- ↑ Jonathan Schaeffer (1997, 2009). One Jump Ahead. 7. The Case for the Prosecution, pp. 111-114
- ↑ Bruce Abramson (1990). Expected-Outcome: A General Model of Static Evaluation. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 12, No. 2
- ↑ Loss function - Use in statistics - Wkipedia
- ↑ "Using cross-entropy error function instead of sum of squares leads to faster training and improved generalization", from Sargur Srihari, Neural Network Training (pdf)
- ↑ Michael Buro (1995). Statistical Feature Combination for the Evaluation of Game Positions. JAIR, Vol. 3
- ↑ Donald H. Mitchell (1984). Using Features to Evaluate Positions in Experts' and Novices' Othello Games. Masters thesis, Department of Psychology, Northwestern University, Evanston, IL
- ↑ Jens Christensen (1986). Learning Static Evaluation Functions by Linear Regression. in Tom Mitchell, Jaime Carbonell, Ryszard Michalski (1986). Machine Learning: A Guide to Current Research. The Kluwer International Series in Engineering and Computer Science, Vol. 12
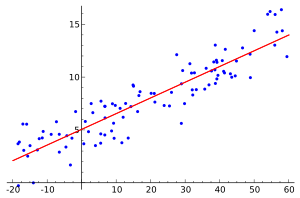
- ↑ Random data points and their linear regression. Created with Sage by Sewaqu, November 5, 2010, Wikimedia Commons
- ↑ Re: Piece weights with regression analysis (in Russian) by Fabien Letouzey, CCC, May 04, 2015
- ↑ Michael Buro (1995). Statistical Feature Combination for the Evaluation of Game Positions. JAIR, Vol. 3
- ↑ LOGISTELLO's Homepage
- ↑ Re: Insanity... or Tal style? by Miguel A. Ballicora, CCC, April 02, 2009
- ↑ Amir Ban (2012). Automatic Learning of Evaluation, with Applications to Computer Chess. Discussion Paper 613, The Hebrew University of Jerusalem - Center for the Study of Rationality, Givat Ram
- ↑ Re: How Do You Automatically Tune Your Evaluation Tables by Álvaro Begué, CCC, January 08, 2014
- ↑ The texel evaluation function optimization algorithm by Peter Österlund, CCC, January 31, 2014
- ↑ Определяем веса шахматных фигур регрессионным анализом / Хабрахабр by WinPooh, April 27, 2015 (Russian)
- ↑ Piece weights with regression analysis (in Russian) by Vladimir Medvedev, CCC, April 30, 2015
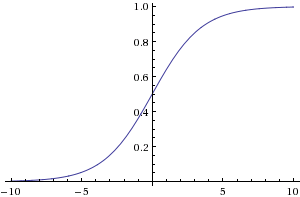
- ↑ log-linear 1 / (1 + 10^(-s/4)) , s=-10 to 10 from Wolfram|Alpha
- ↑ SPSA Tuner for Stockfish Chess Engine by Joona Kiiski
- ↑ MATLAB from Wikipedia
- ↑ CLOP for Noisy Black-Box Parameter Optimization by Rémi Coulom, CCC, September 01, 2011
- ↑ CLOP slides by Rémi Coulom, CCC, November 03, 2011
- ↑ thesis on eval function learning in Arimaa by Jon Dart, CCC, December 04, 2015
- ↑ MMTO for evaluation learning by Jon Dart, CCC, January 25, 2015
- ↑ Broyden–Fletcher–Goldfarb–Shanno algorithm from Wikipedia
- ↑ Arasan 19.2 by Jon Dart, CCC, November 03, 2016 » Arasan's Tuning
- ↑ Limited-memory BFGS from Wikipedia
- ↑ Re: CLOP: when to stop? by Álvaro Begué, CCC, November 08, 2016
- ↑ Re: Texel tuning method question by Jon Dart, CCC, July 23, 2017
- ↑ Thomas Anantharaman (1997). Evaluation Tuning for Computer Chess: Linear Discriminant Methods. ICCA Journal, Vol. 20, No. 4
- ↑ The texel evaluation function optimization algorithm by Peter Österlund, CCC, January 31, 2014
- ↑ Rémi Coulom (2011). CLOP: Confident Local Optimization for Noisy Black-Box Parameter Tuning. Advances in Computer Games 13
- ↑ Amir Ban (2012). Automatic Learning of Evaluation, with Applications to Computer Chess. Discussion Paper 613, The Hebrew University of Jerusalem - Center for the Study of Rationality, Givat Ram
- ↑ Kunihito Hoki, Tomoyuki Kaneko (2014). Large-Scale Optimization for Evaluation Functions with Minimax Search. JAIR Vol. 49, pdf
- ↑ brtzsnr / txt — Bitbucket by Alexandru Mosoi
- ↑ Home — TensorFlow
- ↑ Limited-memory BFGS from Wikipedia
- ↑ alonamaloh / ruy_tune — Bitbucket by Álvaro Begué
- ↑ Maximum likelihood estimation from Wikipedia
- ↑ Jacobian matrix and determinant from WIkipedia
- ↑ Introducing PET by Ed Schröder, CCC, June 27, 2018
- ↑ Tool for automatic black-box parameter optimization released by Rémi Coulom, CCC, June 20, 2010
- ↑ CLOP for Noisy Black-Box Parameter Optimization by Rémi Coulom, CCC, September 01, 2011
- ↑ Re: CLOP: when to stop? by Álvaro Begué, CCC, November 08, 2016
- ↑ Re: Eval tuning - any open source engines with GA or PBIL? by Jon Dart, CCC, December 06, 2014
- ↑ Re: The texel evaluation function optimization algorithm by Jon Dart, CCC, March 12, 2014
- ↑ Eval tuning - any open source engines with GA or PBIL? by Hrvoje Horvatic, CCC, December 04, 2014
- ↑ ROCK* black-box optimizer for chess by Jon Dart, CCC, August 31, 2017